CONTENIDO
Geometr�a junto al r�o
Geometr�a a campo raso
Geometr�a de viaje
Sin tablas ni f�rmulas
Donde la Tierra se junta con el Cielo
Geometr�a de los robinsones
Geometr�a a ciegas
Lo antiguo y nuevo sobre el c�rculo
Geometr�a sin mediciones y sin c�lculos
Grande y peque�o en geometr�a
Econom�a Geom�trica
Bajar parte 2
Bajar parte 3
Escribir @ Antonio

GEOMETRIA RECREATIVA
PARTE PRIMERA
GEOMETRIA AL AIRE LIBRE
PARTE PRIMERA
GEOMETRIA AL AIRE LIBRE

Cap�tulo Primero
Geometr�a en el Bosque
|
El idioma de la naturaleza es matem�tica, letra de esta lengua, son los
c�rculos, tri�ngulos y otras figuras geom�tricas.
Galileo. |
1. Por longitud de la sombra.
2. Dos modos mas
3. El modo de Julio Verne
4. Como actu� el coronel
5. Con ayuda de una agenda
6. Sin acercarse al �rbol
7. El alt�metro de los silvicultores.
8. Con ayuda del espejo
9. Dos pinos
10. La forma del tronco
11. Un gigante a seis patas.
1. Por longitud de la sombra.
Todav�a recuerdo esa atenci�n, con la que yo estuve mirando por primera vez a un canoso guardabosque, el que estando junto a un pino grande, ha medido su altura con un aparato de bolsillo. Cuando �l apunt� con una tablilla cuadrada en la cima del �rbol, yo esperaba, que el viejo subiera con una cadena para medir, en lugar de ello, �l volvi� a meter en el bolsillo el aparato y dijo que la medici�n estaba terminada. Yo pensaba que por el momento no hab�a comenzado�
En aquel tiempo yo era muy joven y esa manera de medir, cuando la persona establece la altura del �rbol sin cortarlo o sin subirse a �l, me parec�a como un milagro pequeño. Tan solo mas tarde, cuando tuve las primeras naciones geom�tricas, he entendido, como es de f�cil hacer ese tipo de milagros.
Existen muchas maneras distintas de realizar semejantes mediciones con ayuda unos aparatos sin pretensi�n y sin mecanismos especiales.
Un modo que es muy f�cil y muy antiguo, sin duda, que con �l, el sabio griego Falos, seis siglos antes de Cristo, defini� en Egipto la altura de la pir�mide. Él aprovech� la sombra suya. Los sacerdotes y fara�n, reuni�ndose al pie de la pir�mide, miraban confusamente al extranjero, adivinando por la sombra la altura de la gran construcci�n. Falos, dice la leyenda, eligi� el d�a cuando la longitud de su sombra era igual a su altura, en el mismo momento, la altura de la pir�mide ten�a que ser iguala a la longitud de su sombra. Es el �nico caso, cuando la persona aprovecha su sombra.
La tarea del sabio griego nos parece ahora infantil, f�cil, pero no tenemos que olvidar, que estamos mirando desde la altura del edificio geom�trico, levantado despu�s de Falos. Él vivi� mucho tiempo antes del Euclides, que es el autor del libro famoso, con el cual estudiaron la geometr�a durante dos siglos, despu�s de su fallecimiento. En concreto, las verdades del libro que ahora las conoce cualquier alumno, no estaban descubiertas en la �poca de Falos. Y aprovech�ndose de la sombra para resolver la tarea sobre la altura de la pir�mide, necesitaba saber algunas caracter�sticas geom�tricas del tri�ngulo, pr�cticamente las dos siguientes (Falos fue el primero en enunciar estos principios):
- Los �ngulos sobre la base de un tri�ngulo is�sceles, son iguales, e inversamente, los lados, opuestos a los �ngulos iguales del tri�ngulo is�sceles, son iguales.
- La suma de los �ngulos de cualquier tri�ngulo (el tri�ngulo rect�ngulo es un caso particular), es igual a dos �ngulos rectos.
Con ayuda de ese m�todo, que nos parece tan simple, durante un d�a soleado podemos hacer mediciones de cualquier �rbol aislado, cuando su sombra no se une con la sombra de otro. Pero en nuestras latitudes (San Petersburgo est� en la latitud 60�N y El Cairo, 30�N) no es tan f�cil elegir un buen momento como en Egipto; el Sol se presenta muy bajo sobre el horizonte, y las sombras pueden ser iguales a la altura de sus objetos, solo durante el verano y en torno al mediod�a. Por eso el modo del Falos no es siempre c�modo para llevar a la practica.
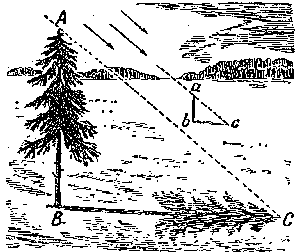
No es dif�cil calcular la altura de una manera un poco distinta, cuando en cualquier d�a soleado se puede usar la sombra, no importando su longitud. Se puede medir su propia sombra o la de una p�rtiga enterrada verticalmente en un suelo plano y calcular la altura buscada con la proporci�n siguiente (figura 1):
Es decir, la altura del �rbol en cuantas veces mayor que la altura de Ud. (o la altura de la p�rtiga), en tantas veces la sombra del �rbol es m�s larga de la sombra Ud. (o la sombra de la p�rtiga). Esto se deduce de la semejanza geom�trica de los tri�ngulos ABC y abc (por dos �ngulos).
|
| Figura 1. Medici�n de la altura de un �rbol por su sombra |
Algunos lectores replican, pues, que esta manera es tan elemental que no necesita argumentaci�n geom�trica. �Es posible que sin geometr�a, quede claro, en cu�ntas veces un �rbol es m�s alto, en tantas veces como su sombra es mas larga? Ocurre que no es tan f�cil como parece. Intente llevar a la pr�ctica esta regla de la sombra, proyectando una con la luz de una l�mpara, ver� que no se cumple.
En la figura 2 se ve el poste AB m�s alto que la columna pequeña ab , aproximadamente al triple, y la sombra del poste m�s larga que la sombra de la columna ( BC : bc ) unas ocho veces. Explicar por qu� en una ocasi�n podemos emplear el modo, y en otro no; sin geometr�a no es posible.
Problema
Vamos a ver d�nde est� la diferencia. Lo que pasa es que los rayos de Sol son paralelos entre ellos, los rayos de farola no son paralelos. Esto �ltimo est� claro, pero �c�mo que los rayos de Sol son paralelos, cuando ellos, sin duda, est�n cruz�ndose en el mismo lugar de donde est�n saliendo?
Soluci�n
Los rayos de Sol, cayendo sobre la Tierra, los podemos considerar paralelos, porque el �ngulo entre ellos es muy pequeño, pr�cticamente imperceptible. Un simple c�lculo geom�trico puede aclarar la situaci�n confusa. Imag�nese dos rayos saliendo desde cualquier punto del Sol y cayendo sobre la Tierra a una distancia entre ellos de un kil�metro mas o menos. Entonces, si ponemos una pata del comp�s en el punto del Sol y hacemos una circunferencia de radio igual a distancia entre el Sol y Tierra (150.000.000 km), entonces nuestros dos rayos�radios sostienen un arco justo de un kilometro de longitud.
La longitud total de esta gigantesca circunferencia igual a
Un grado de ella, evidentemente, es 360 veces menor, es decir, mas o menos 2.600.000 km; Un minuto de arco es 60 veces menor del grado, es igual a 43.000 km, y un segundo de arco en 60 veces menor, es igual 720 km. Pero nuestro arco tiene la longitud de 1 km; es decir, corresponde al �ngulo 1/720 segundos. Ese �ngulo es imperceptible, incluso para aparatos astron�micos; por lo tanto, pr�cticamente podemos considerar que los rayos de Sol, caen a la Tierra en forma paralela.

|
| Figura 2. Cuando el mismo modo de medici�n es imposible. |
Sin consideraciones geom�tricas no podemos argumentar el modo examinado, haciendo la proporci�n de la altura por su sombra.
Si llevamos a la pr�ctica el sistema de las sombras, constataremos su inexactitud. Las sombras no son limitadas de manera precisa; ellas tienen un contorno difuso por lo que su l�mite es indeterminado.
Esto ocurre, porque el Sol no es un punto, es un gran cuerpo luminiscente, emite los rayos desde m�s de un punto.
La Figura 3 indica por qu� la sombra BC del �rbol tiene una adici�n de la penumbra CD, el que poquito a poco desaparecer�. El �ngulo CAD entre los limites de la penumbra corresponden al �ngulo, sobre el que siempre podemos ver el disco de Sol, es decir, mitad de un grado. Aparecer� un error, por que tendremos dos sombras, ambas correctas. Este error puede alcanzar un 5% o m�s, si la posici�n del sol es baja, ambas sombras sean medidas no exactamente correcto, con un bajo estado de Sol procede alanzar 5% y m�s.

|
| Figura 3. C�mo aparece la sombra |
A estos errores se le unen otros, como por ejemplo, accidentes del terreno, y el resultado es poco seguro. En los sitios montañosos este modo es inaplicable.
Volver
2. Dos modos mas
Es muy posible hacer mediciones de la altura sin ayuda de las sombras. Existen muchas maneras; empezaremos con dos f�ciles.
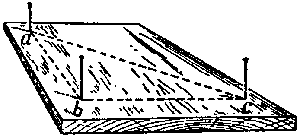
Antes de todo podemos utilizar las propiedades del tri�ngulo rect�ngulo is�sceles, aprovechando un simple aparato, lo cual es f�cil de preparar a trav�s de una tablilla y tres alfileres. Sobre una tablilla lisa marcamos tres puntos, los v�rtices del tri�ngulo rect�ngulo is�sceles, en los puntillos clavamos alfileres (Figura 4). Si no tiene escuadra y comp�s para dibujar el tri�ngulo, entonces puede coger el papel, lo dobla una vez, despu�s lo dobla transversalmente al primer doblez, de modo que ambas partes del primer doblez se unen, y se obtiene el �ngulo recto. El mismo papel puede ser �til para medir los trozos iguales.
|
| Figura 4. El aparato de alfileres para la medici�n a las alturas |
Como vemos, el aparato lo podemos preparar en distintas formas.
Utilizar este aparato es tan f�cil como prepararlo. Alej�ndose del �rbol, teniendo el aparato de modo que uno de los catetos del tri�ngulo apunte verticalmente, para facilitar la observaci�n, podemos utilizar una plomada (un hilo con un objeto pesado atado a un extremo) atada al alfiler superior.
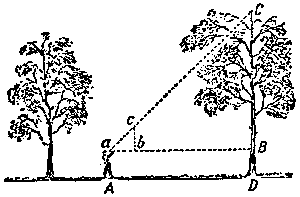
Acerc�ndose al �rbol o alej�ndose de �l, Ud. siempre encontrar� un sitio A (Figura 5), desde cual, mirando a los alfileres a y c, ver�n, que ellos tapar�n la cima C del �rbol: eso significa que la prolongaci�n de la hipotenusa ac pasa por el punto C . Como ya lo hemos visto en el ejemplo anterior, la separaci�n entre ab es igual a CB , ya que el �ngulo a = 45�.
Por consecuencia, acabando de medir el trazo aB y añadir BD , es decir, elevaci�n aA del ojo sobre el fondo, recibimos la altitud buscada del �rbol.
|
| Figura 5. Esquema del uso al aparato de alfileres |
|
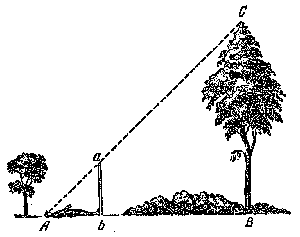
| Figura 6. Un modo mas para medir la altura. |
es la altura buscada del �rbol
Volver
3. El modo de Julio Verne
El siguiente modo tampoco es dif�cil. La manera de medir los objetos altos lo describi� en su novela "La isla misteriosa" Julio Verne:
�Hoy vamos a medir la altura de una plazoleta de la Vista Lejana, �dijo el ingeniero.
�� Necesitamos algunos instrumentos? �pregunt� Gebert.
�No hace falta. Lo haremos de otra manera, m�s f�cil y m�s segura.
El joven, aplicadamente sigue detr�s baj�ndose desde el muro hasta la orilla. Cogiendo una p�rtiga de 12 pies de longitud, el ingeniero lo hizo exacto, comprob�ndolo con su estatura, la cual sabia muy bien. Gebert le trajo una plomada, dada por el ingeniero; fue una piedra atada al extremo de una cuerda. Acerc�ndose 500 pies al muro gran�tico y vertical, el ingeniero clav� la p�rtiga, verticalmente con la ayuda de la plomada, en la arena. Un poco despu�s se alej� tanto de la p�rtiga, que tumb�ndose pudo ver el extremo de la p�rtiga y la cresta de montaña sobre una l�nea recta (Figura 7). Este punto lo marc� con un palito.
��Tienes algunas nociones geom�tricas?�pregunt� a Gebert.
�S�.
��Recuerdas las propiedades de los tri�ngulos semejantes?
� Sus lados an�logos son proporcionales.
�Exacto. Ahora voy a construir dos tri�ngulos rect�ngulos semejantes. El cateto del pequeño sea la p�rtiga, el otro cateto, sea la distancia desde el palillo hasta el pie de la p�rtiga; la hipotenusa, es la l�nea de mi vista. En el tri�ngulo mayor los catetos son la muralla, la altura que queremos medir, y la distancia desde el palillo hasta el pie de la muralla; hipotenusa es la l�nea de mi vista, uni�ndose con la hipotenusa tri�ngulo menor.
��He entendido! � exclam� el joven. El trayecto del palillo hasta la p�rtiga corresponde as� al trayecto desde el palillo hasta el pie de la muralla, como la altura de la p�rtiga a la altura de la muralla.
�Exactamente. Sigamos, si medimos las dos distancias primeras, y sabiendo la altura de la p�rtiga, podemos calcular el cuarto miembro de la proporci�n que es la altura de muralla.
Ambas l�neas horizontales fueron medidas: la pequeña es de 15 pies, la grande es de 500 pies.
Al fin el ingeniero lo hizo anotaci�n:
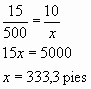
Entonces, la altura de la muralla es 333 pies.

|
| Figura 7. Como encontraban la altura de un acantilado, los personajes de Julio Verne |
Volver
4. Como actu� el coronel
Algunos modos, descritos anteriormente, no son c�modos por la necesidad de tumbarse sobre la tierra. Pero ese tipo de incomodidades las podemos evitar.
As� ha ocurrido un d�a en un frente durante la Segunda Guerra Mundial. A la subdivisi�n del teniente Ivanov le mandaron a construir un puente por encima de un r�o de montaña, enfrente del lugar donde desembarc� el enemigo.
Para reconocimiento de un terreno boscoso, mandaron un grupo de b�squeda con el mayor coronel Papov�En el monte cercano ellos midieron el di�metro y las alturas de los arboles m�s t�picas de aquella zona, establecieron la cuenta de los arboles �tiles.
Establecieron las alturas de los arboles con ayuda de una jal�n, como indica la Figura 8.
Explicaci�n del modo.
Necesitamos una p�rtiga mucho alta que nuestra propia estatura, la clavamos en la tierra a cierta distancia del �rbol (Figura 8). Alej�ndose atr�s de la p�rtiga, a continuaci�n Dd hasta el sitio A, desde cual, mirando a la copa del �rbol, veremos el punto superior b de la p�rtiga, sobre la una l�nea recta. Despu�s, sin cambiar la posici�n la cabeza, se mira en el sentido de una l�nea recta horizontal aC, marcando los puntos c y C, donde la l�nea de la vista encuentra la p�rtiga y el tronco. Piden al ayudante hacer las marcas en aquellos puntos, y la observaci�n se ha terminado. Solo es necesario, en virtud de la semejanza de los tri�ngulos abc y aBC, calcular BC de la proporci�n.
Donde
Las distancias bc, aC y ac son f�ciles de medir inmediatamente. Al resultado de tamaño BC añadir la distancia CD, para encontrar la altura buscada.
Para la determinaci�n de la cantidad de los arboles, el coronel dio �rdenes a los soldados de medir la superficie del bosque. Despu�s calcul� la cantidad de arboles dentro de un terreno 50 ´ 50 metros cuadrados e hizo los c�lculos correspondientes.
De todos los datos recogidos, el coronel ha puesto en orden las cosas, d�nde y c�mo construir mejor el puente, el que fue construido r�pidamente y la misi�n de combate fue cumplida.
Volver
5. Con ayuda de una agenda
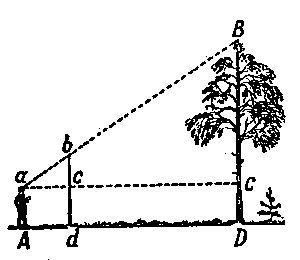
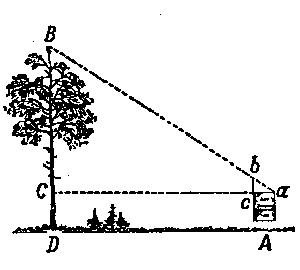
En otro lugar, para tener los resultados aproximados de las alturas inaccesibles, podemos utilizar nuestra agenda y un l�piz. Ella nos ayuda a construir en el espacio dos tri�ngulos semejantes, desde cuales obtenemos la altura buscada. Sujetamos la libreta cerca de los ojos, como indica la Figura 9. Ella tiene que estar en plano vertical y el l�piz sobresaliendo encima del canto de libreta tanto, que mirando desde el punto a, ver la cima B del �rbol tapado por la punta b del l�piz. Como consecuencia de los tri�ngulos semejantes abc y ABC, la altura BC determina de la proporci�n:
|
| Figura 8. Medici�n de altura con la ayuda de una p�rtiga. |
|
| Figura 9. Medici�n de altura con la ayuda de una agenda. |
Las distancias bc, ac y aC se miden inmediatamente. Al resultado de tamaño BC es necesario añadir la longitud CD, es decir, en un sitio plano, la altura de los ojos sobre el piso.
Como la anchura de la agenda es invariable, y si nosotros siempre vamos a estar a la misma distancia del �rbol (por ejemplo 10 m ), la altura depender� solo del parte sobresalida bc de l�piz. Por eso se puede hacer antes el c�lculo, a cu�l la altura corresponde una u otra altura bc sobresaliente, y marcar estas cifras sobre el l�piz. La agenda se convierte a un alt�metro, con su ayuda se puede definir la altura inmediatamente, sin c�lculos.
Volver
6. Sin acercarse al �rbol
Algunas veces, por cualquier causalidad, no podemos acercarse justo al pie del �rbol. �Podemos en esta ocasi�n determinar su altura?
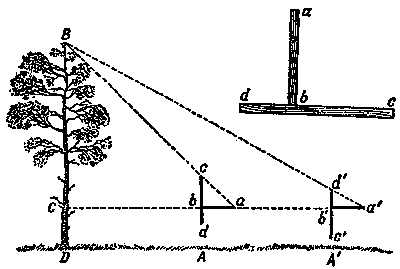
|
| Figura 10. Uso de un alt�metro, construido solo con dos tablillas. |
Es posible. Para eso inventaron un aparato muy ingenioso, el que, como aparatos anteriores, es f�cil de preparar. Dos tablillas ab y cd (Figura 10) se fijan en �ngulo recto de modo que ab sea igual bc, y bd sea la mitad de ab. Es todo el truco.
|
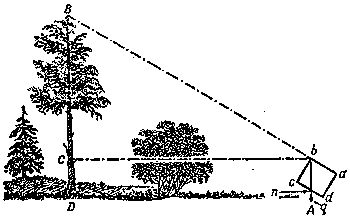
| Figura 11. Esquema del uso al alt�metro de los silvicultores. |
Para poder medir, se mantiene el aparato en los manos, apuntando la tablilla cd verticalmente (para eso existe una plomada, el cordoncillo con el plomo), y se ubica sucesivamente en dos sitios: primero (figura 10) en el punto A, donde se sostiene el aparato con la punta c hacia arriba, y despu�s en el punto A' , m�s alejado, donde el aparato donde el aparato se sostiene con la punta d hacia arriba. El punto A se elige as�: mirando desde el punto a al punto c, en l�nea con la cima del �rbol. El punto A' se busca as�: mirando desde el punto a al punto d, en l�nea con la cima del �rbol. La distancia entre los puntos A y A', es igual a la altura BC del �rbol. La igualdad se deduce de
y
entonces,
Como se ve, utilizando este aparato tan simple, medimos el �rbol, sin acercarnos a su base m�s que a la distancia igual que su altura. Se supone, que si es posible acercarse al tronco, entonces, es suficiente encontrar un punto A o A' para saber su altura.
En lugar de dos tablillas podemos utilizar dos alfileres, situ�ndolos apropiadamente sobre una tabla. As� el "aparato" mucho m�s simple.
Volver
7. El alt�metro de los silvicultores.
Casi es la hora de explicar, como son hechos los "verdaderos" alt�metros, los que utilizan los silvicultores. Describo un alt�metro semejante, un poco modificado, para poderlo construir por s� mismo. El sentido de estructura se ve en la figura 11.

|
| Figura 12. El alt�metro de los silvicultores |
Se hace un rect�ngulo abcd, de cart�n o madera para sostener en las manos, mirando a lo largo del borde ab, aline�ndole con la cima B del �rbol. El punto b tiene colgado una plomada q . Se marca el punto n, en el cual el hilo cruza la l�nea dc. Los tri�ngulos bBC y bnc son semejantes, y como ambos son rect�ngulos y tienen los �ngulos agudos igualdades bBC y bnc (conforme con los lados paralelos), entonces podemos escribir la proporci�n
De aqu� se desprende
Como bC, nc y bc son conocidos, entonces es f�cil de encontrar la altura buscada del �rbol, añadiendo la distancia de la parte baja del tronco CD ( la altura del instrumento sobre la tierra).
Falta añadir algunos detalles. Si el borde bc de la tabla es igual, por ejemplo, a 10 cm, marcando las divisiones del cent�metro, pues la proporci�n nc/bc siempre va a expresarse como fracci�n decimal, indicar� directamente la fracci�n de la distancia bC , que es la altura BC del �rbol.
Sea, por ejemplo, el hilo se ubic� enfrente la divisi�n s�ptima (es nc= 7 cm); es decir, que la altura del �rbol sobre nivel del ojo equivale a 0,7 veces la distancia del observador hasta el tronco.
Otro mejoramiento se refiere al modo de la observaci�n: para que sea c�modo mirar a lo largo de la l�nea ab, podemos doblar sobre los �ngulos superiores del rect�ngulo (es de cart�n) dos cuadrados agujereados: Un agujero, para el ojo, el otro m�s grande, para apuntar la cima del �rbol (figura 12).
El perfeccionamiento siguiente se representa en un aparato, el que se muestra en su tamaño natural en la figura 12. Preparar el aparato es f�cil y consume poco tiempo. No necesita mucho sitio en el bolsillo y durante la excursi�n da la posibilidad r�pida de definir las alturas de los objetos, como los arboles, edificios y etc. (El instrumento esta dentro del compuesto preparado por el autor del libro "Geometr�a en el aire libre")
Problema
�Es posible con ayuda del aquel alt�metro, anteriormente descrito, medir los arboles, sin ninguna posibilidad de acercarse? �Si es posible, entonces c�mo tenemos que actuar?
|
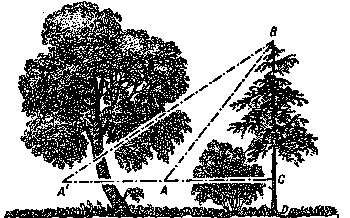
| Figura 13. Como medir la altura de un �rbol, sin acercarse hacia �l |
Soluci�n
Necesita apuntar el aparato justo la cima B del �rbol (figura 13) desde los dos puntos A y A'. Una vez que est� determinado A ,
y en el punto A' que
Entonces, ya sabemos, que
y
donde
o
Se ve que midiendo la distancia AA' entre ambos sitios de observaci�n y cogiendo la divisi�n necesaria de esta cantidad, se puede encontrar la altura buscada.
Volver
8. Con ayuda del espejo
Problema
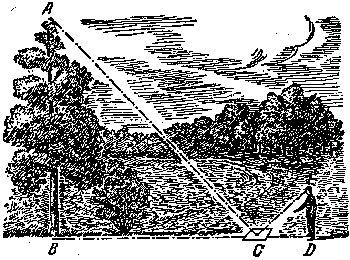
Un modo mas para determinar la altura de un �rbol con ayuda del espejo. A cualquier distancia (figura 14) desde el �rbol, sobre un piso llano en el punto C se pone el espejo horizontalmente y alejan hacia atr�s hasta un punto D , en el cual el observador ve la cima A del �rbol en el espejo. Por lo tanto el �rbol AB es tantas veces m�s alto que la estatura del observador ED , en las veces que la distancia BC desde el espejo hasta el �rbol es m�s grande que la distancia CD desde el espejo hasta el observador. �Por qu�?
|
| Figura 14 Medici�n de altura con la ayuda de un espejo . |
Soluci�n
El modo est� fundado en la ley de la reflexi�n de la luz. El punto superior A (figura 15) se refleja en el punto A' as�, que AB = A'B. Dada la semejanza de los tri�ngulos BCA' y CED se deduce, que
En esta proporci�n queda solo cambiar A'B igualado a AB, para argumentar la proporci�n de la tarea.
Esta manera c�moda podemos utilizar en cualquier tiempo, pero no en el bosque frondoso.
Problema
�C�mo tenemos que proceder, cuando no podemos acercarnos al �rbol que queremos medir?

|
| Figura 15. Construcci�n geom�trica para el modo de medir las alturas con ayuda del espejo |
Soluci�n
Esta antigua tarea, tiene ya, como 500 años. Ella la examin� un matem�tico de la Edad Media, Antonio de Cremona en su obra "Geodesia Pr�ctica"(año 1400).
La tarea se soluciona con la doble aplicaci�n del modo anteriormente descrito, poniendo el espejo en dos sitios. Haciendo la construcci�n correspondiente, no es dif�cil por semejanza de los tri�ngulos deducir que la altura buscada del �rbol es igual a la elevaci�n del ojo del observador, multiplicado por la proporci�n de la distancia entre las dos posiciones del espejo hasta la diferencia las distancias entre el observador y el espejo.
Antes de terminar nuestro di�logo sobre la medici�n de los arboles, propongo a los lectores una tarea mas "desde el bosque".
|
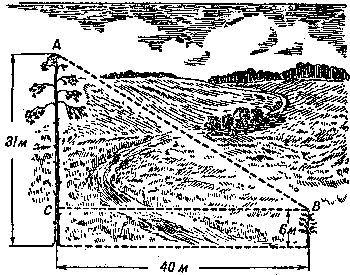
| Figura 16. La distancia entre los v�rtices de los pinos |
9. Dos pinos
Problema
La distancia entre dos pinos es de 40 m. Sus alturas son: 31 m y solo 6 m. �Pueden calcular la distancia entre sus cimas?
Soluci�n
La distancia buscada entre las cimas de los pinos (figura 16) por el teorema de Pit�goras es:
Volver
10. La forma del tronco
Ahora, paseando por el bosque podr�an determinar la altura de cualquier �rbol, por la media decena de las maneras. Ser�a interesante tambi�n determinar su volumen, calcular cu�ntos metros c�bicos de madera tiene, y adem�s pesar , para saber si es posible llevar este tronco solo con ayuda de un carro de cuatro ruedas. Ambas tareas no son tan f�ciles, como las anteriores; los especialistas no encontraron la soluci�n precisa y est�n contentos con una evaluaci�n aproximadamente. Incluso el tronco cortado y limpio de ramas, la tarea no se soluciona f�cilmente
Lo que pasa es que un tronco del �rbol, incluso liso, sin anchuras, no representa ni un cilindro, ni un cono, ni cono truncado, ni otro cuerpo geom�trico, cuyo volumen lo podemos calcular a trav�s de las f�rmulas. El tronco, est� claro, no es un cilindro, �l se estrecha hacia la cima, pero tampoco es cono, porque su generatriz no es la l�nea recta, es una l�nea curva, adem�s no es arco de circunferencia, como tampoco es otra l�nea curva, convexa hacia el eje de un �rbol.
Por eso, el c�lculo de volumen exacto es realizado solo con ayuda del calculo integral. Para algunos lectores le parece extraño, que para la medici�n de una simple viga tenemos que dirigirnos a la matem�tica superior. La mayor�a pensa, que la matem�tica superior no tiene mayor relaci�n con la vida corriente y s�lo se relaciona con algunos temas especiales. Absolutamente no es as�: puede ser muy correcto medir el volumen de una estrella o planeta, utilizando la geometr�a elemental, mientras tanto el calculo exacto del volumen a una viga o barrica no es posible sin geometr�a anal�tica o c�lculo integral.
Pero nuestro libro no propone a los lectores los conocimientos de la matem�tica superior; por eso quedaremos satisfecho con el c�lculo aproximado del volumen de un tronco. Vamos a suponer que el volumen de un tronco es aproximadamente equivalente al volumen del tronco de cono, y para el tronco completo, incluyendo su cima, el volumen del cono, o por fin, para las vigas cortas, al cilindro. El volumen de cada uno de los tres cuerpos es f�cil de calcular. �Es posible para uniformidad de c�lculo, encontrar una f�rmula del volumen, que sea v�lida para los tres cuerpos indicados?
Despu�s calcularemos aproximadamente el volumen del tronco, y no nos interesaremos si se parece m�s a un cilindro, un cono perfecto o truncado.
Evidentemente la formula existe; mas que ella es beneficiosa, no solo para el cilindro, el cono perfecto, o truncado, si no tambi�n para una prisma, las pir�mides perfectas o truncadas y tambi�n para la esfera. Esta formula perfecta conocida por el nombre de la formula de Simpson:
donde:
h = la altura del cuerpo,
b 1 = la superficie de la cara inferior,
b 2 = la superficie la secci�n media,
b 3 = la superficie de la cara superior.
Demostrar, que con ayuda de la formula de Simpson se puede calcular el volumen de los siete cuerpos siguientes: del prisma, la pir�mide perfecta, la pir�mide truncada, el cono perfecto, el cono truncado y de la esfera.
Soluci�n
Estando seguro de la exactitud de esta formula es f�cil su la aplicaci�n a los cuerpos enumerados. Entonces para el prisma y el cilindro (Figura 17a)
para la pir�mide y el cono (Figura 17, b)
para el cono truncado (Figura 17, c)

Para la pir�mide truncada el c�lculo es semejante.
Por fin, para la esfera (Figura 17, d)
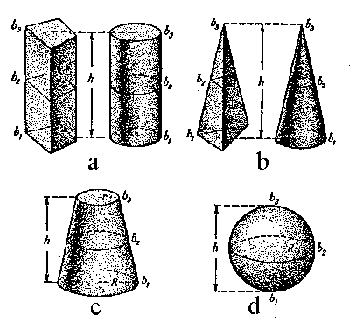
|
| Figura 17. Los cuerpos geom�tricos, cuyos vol�menes se pueden calcular con la f�rmula universal |
Problema
Anotamos otra caracter�stica muy interesante de nuestra formula universal: ella es v�lida para calcular la superficie de las figuras planas : el paralelogramo, el trapecio y tri�ngulo, si:
h = la altura de la figura,
b 1 = la longitud del lado inferior,
b 2 = la longitud de la media,
b 3 = la longitud del lado superior
�C�mo lo demostramos?
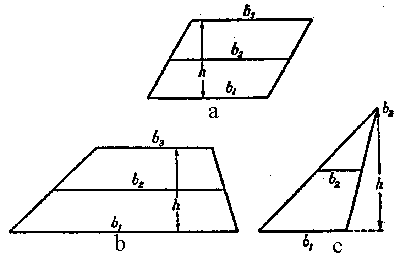
|
| Figura 18. La f�rmula universal para calcular las superficies de estas figuras |
Soluci�n
Utilizando la formula, tenemos:
Para el paralelogramo (cuadrado, rect�ngulo) (Figura 18, a)
para tri�ngulo (Figura 18, c)
Como ven, la formula tiene el suficiente derecho de llamarse universal.
El volumen y el peso del �rbol (antes de ser talado)
Pues tienen a su disposici�n la f�rmula, con la ayuda de cual pueden aproximadamente calcular el volumen del tronco cortado, sin preocuparse y sin preguntar a qu� cuerpo geom�trico se parece, si al cilindro, o al cono perfecto o al cono truncado.
Para esto necesitamos las cuatro dimensiones, la longitud del tronco y los tres di�metros: el corte de abajo, de arriba y el de la longitud media. La medici�n de los di�metros extremos es muy f�cil; la determinaci�n inmediata del di�metro mediano sin instrumentos especiales (escala de los leñadores, Figura 19 y 20) es bastante incomoda. Pero la complejidad la podemos evitar, si medimos la circunferencia del tronco con un cordel y dividimos su longitud por

|
| Figura 19. Midiendo el di�metro del �rbol con escal�metro |
El volumen del �rbol cortado, es suficientemente exacto para los objetivos pr�cticos.
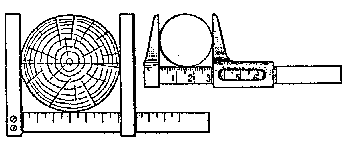
|
| Figura 20. Escala y escal�metro |
Brevemente, con menos exactitud se soluciona esta tarea, si calculamos el volumen del tronco, como el volumen del cilindro, el di�metro del extremo es igual al di�metro por el medio de longitud: el resultado obtenido es menor a veces hasta en un 12 % . Pero si dividimos el tronco mentalmente en secciones de dos metros de longitud cada uno, y determinamos el volumen de cada una, como si fueran cilindros, entonces el resultado ser� mucho mejor, con un error de 2 a 3%.
Todo esto, sin embargo, no es aplicable al �rbol crecido: si no deciden subirse a �l, entonces s�lo podr�n medir la parte de abajo. En ese caso, nos contentaremos con un valor aproximado, sabiendo que los silvicultores profesionales act�an habitualmente de la misma manera.
Para esos casos ellos usan una tabla, llamada de "los n�meros espec�ficos", es decir los n�meros muestran, cual parte del volumen de �rbol medido forman el volumen del cilindro de la misma altura y el di�metro, medido sobre el nivel de pecho de una persona, es 1,30 cm (este tamaño es m�s c�modo medir).

|
| Figura 21. Los n�meros muestran, cual parte del volumen de �rbol medido forman el volumen del cilindro de la misma altura y el di�metro, medido sobre el nivel de pecho de una persona, es 1,30 cm (este tamaño es m�s c�modo medir). |
El Figura 21 explica lo anteriormente dicho. Por supuesto, "los n�meros espec�ficos" son distintos para los arboles de altitud y de rasa diferente, as� como la forma del tronco es inconstante. Pero las variaciones no son muy grandes: para el tronco de un pino o para el abeto (crecido en bosque frondoso) "los n�meros espec�ficos" son entre los 0,45 y 0,51 , es decir mas o menos igual a su mitad.
Entonces, sin equivocaci�n podemos obtener el volumen de un �rbol con�fero como la mitad del volumen de cilindro de la misma altura con el di�metro, sea igualado el corto de �rbol sobre un nivel de pecho.
Evidentemente, es solamente un volumen aproximado, pero no muy lejos del resultado autentico: entre un 2% de sobredimensi�n y hasta un 10% de subdimensi�n.
Entonces solamente queda un paso para valuar el peso de �rbol sobre la ra�z. Para eso es suficiente saber, que 1 metro cubico de una madera fresca del pino o abeto pesa como 600 � 700 kg. Sea por ejemplo, est� Ud. al lado de un abeto, la altura de cual es de 28 m. Y la circunferencia de tronco sobre el nivel de pecho son � 120 cm.
La superficie de c�rculo correspondiente es 1.100 cm 2 o 0,11 m 2 , y el volumen de tronco ser�
Sabiendo que el 1m 3 de madera fresca del abeto pesa ~ 650 kg , encontraremos que el 1,5 m 3 deber�an pesar aproximadamente una tonelada ( 1.000 kg)
Geometr�a de las hojas.
Problema
Debajo de la sombra de �lamo plateado han crecido ramas desde ra�z. Se coge una hoja y se comprueba que ella es m�s grande las hojas del �rbol paterno. Las hojas que crecen en sombra compensan la falta de luz con el tamaño de su superficie. Estudiar este fen�meno es asunto de bot�nica, pero la geometr�a tambi�n aqu� puede decir algo: saber en cu�ntas veces la superficie de la hoja es mas mayor que la superficie de la hoja del �rbol paterno.
�C�mo se solucionara este problema?
Soluci�n
Podemos ir por dos caminos. En primer lugar, determinar la superficie de cada una hoja y encontrar sus proporciones. Medir la superficie de la hoja es posible, tap�ndola con un papel cuadriculado y transparente, donde cada una casilla corresponde, por ejemplo, 4 mm 2 (la hoja cuadriculada y transparente utilizada en la practica se llama "paleta"). Aunque la manera es correcta, pero demasiado minuciosa.
El modo corto se basa que ambas hojas, de diferentes tamaños, tienen la forma mas o menos parecida, es decir, son figuras semejantes. Las superficies de estas figuras, corresponden al cuadrado de sus medidas de longitud.
Entonces, determinando en cu�ntas veces una hoja es m�s larga o m�s ancha que la otra, elevamos el numero al cuadrado y obtendremos la proporci�n sus superficies.
Sea que una hoja de las ra�ces tenga la longitud 15 cm y la hoja paterna solamente 4 cm ; la proporci�n de las longitudes es 15/4 , entonces, al elevar al cuadrado, tendremos 225/16, es decir en 14 veces, que corresponde a las veces que una superficie es mayor a la otra. Redondeando (porque la exactitud absoluta aqu� no puede ser), podremos decir que la hoja del soto es m�s grande que la arb�rea en ~15 veces.
Un ejemplo m�s.
Problema
Creciendo bajo la sombra, una hoja tiene una longitud de 31 cm. En otro ejemplar, creciendo a pleno sol, la longitud de placa es solamente 3,3 cm. �En cuantas veces mas o menos la superficie de primera hoja es mayor que la otra superficie?
Soluci�n
Actuamos sobre antecedente. La proporci�n de las superficies es
Entonces, la hoja grande tiene una superficie mayor a la otra en 90 veces.

|
| Figura 22. Encontrar la proporci�n de las superficies de estas hojas. |
No es dif�cil recoger en el bosque mucho pares de hojas con forma parecida, pero con tamaños distintos y de esta manera recibir un material curioso para las tareas geom�tricas sobra la proporci�n de las superficies de las figuras semejantes.

|
| Figura 23. Encontrar la proporci�n a las superficies de estas hojas. |
Para un ojo desacostumbrado siempre parece extraño, que relativamente una pequeña diferencia en longitud y anchura de las hojas derive una diferencia apreciable en sus superficies. Si, por ejemplo, entre dos hojas, de forma semejante, una mas larga que otra en 20%, entonces la proporci�n de sus superficies ser�
es decir, la diferencia importa 40%. Con la diferencia de la anchura en 40% una hoja supera otra sobre la superficie en
es casi doble.
Problema
Proponemos a los lectores encontrar la proporci�n de las superficies de hojas, representadas en las figuras 23 y 24
Volver
11. Un gigante a seis patas.
�Las hormigas son unas criaturas sorprendentes! Vivamente subiendo sobre un tallo con una carga demasiado pesada para su tamaño tan pequeño (Figura 24), ella le plantea un problema a un observador: �De d�nde ese insecto tiene tanta fuerza, sin demasiado esfuerzo para subir con un peso 10 veces superior del peso de ella misma?
Es que una persona no es capaz de subir por la escalera, con una carga, por ejemplo, como un piano (Figura 24), pero la proporci�n del cargamento sobre el peso de cuerpo es igual como para una hormiga. Resulta, que una hormiga es mas fuerte que el humano.
�Es as�?
Sin geometr�a aqu� no comprendemos.

|
| Figura 24. Un gigante a seis patas. |
Escuchemos antes de todo a un especialista (profesor A. F. Brandt) sobre la fuerza de los m�sculos y despu�s contestamos a la pregunta sobre la proporci�n de las fuerzas de un insecto y de una persona:
�Un m�sculo vivo parece a un cordoncillo el�stico, pero su contracci�n principalmente funciona sobre la influencia de la excitaci�n nerviosa, en la pr�ctica fisiol�gica aplicando una corriente el�ctrica al nervio apropiado o al mismo m�sculo. �Los experimentos se realizan sobre los m�sculos cortados de una rana recientemente muerta. Como los m�sculos de los animales de sangre fr�a mantienen sus propiedades vitales bastante tiempo fuera del organismo, a una temperatura normal. La forma de la prueba es muy simple, se corta un m�sculo de la pata de atr�s, la pantorrilla, junto con un trozo de f�mur, desde el cual comienza el tend�n. Para una prueba este m�sculo resulta m�s c�modo por su tamaño y su forma y por su facilidad de desecaci�n.
�A trav�s del tend�n se pasa un gancho, bajo de cual enganchan una pesa. Si tocamos el m�sculo con el hilo met�lico, pasando desde la pila galv�nica, entonces instant�neamente se contrae, se acorta y levanta el peso. Gradualmente poniendo mas pesas pequeñas suplementarias ya es f�cil decidir cual es la m�xima capacidad de levantamiento muscular. �Atamos ahora dos, tres, cuatro m�sculos iguales en serie y empezaremos r�pidamente a excitarles. Como vemos, con esta manera no conseguimos mayor esfuerzo de levantamiento, pero el peso va a subir mas alto. Pero si juntamos dos, tres, cuatro m�sculos en un atado , entonces, todo el sistema bajo excitaci�n va a subir mayor cantidad del peso.
�El resultado es parecido cuando los m�sculos se unen entre ellos. Entonces, veremos que el esfuerzo de levantamiento muscular depende �nicamente del grosor, es decir, del corte transversal; pero de ninguna manera depende de la longitud o del peso general.
Despu�s de ese desv�o volveremos a las semejanzas geom�tricas, pero en animales de diferente tamaño.
�Imaginamos dos animales; el primero ampliado al doble en todas medidas de longitud del otro; el volumen y peso del cuerpo, y tambi�n de todos los �rganos sea en 8 veces mayor. Todas las medidas superficiales, adem�s recortes transversales de los m�sculos, solamente en 4 veces mayor. Resulta que el esfuerzo muscular, seg�n el crecimiento de animal de la doble longitud y aumentado en ocho veces del cuerpo, se aumenta solamente en cuatro veces, es decir, que el animal se convierte en doblemente m�s d�bil. Fundamentalmente un animal, cual es el triple mas largo (con los cortes transversales en 9 veces m�s anchos y con el peso en 27 veces m�s grande), resulta que es el triple m�s flojo, y aquel, cual al cu�druplo m�s largo es cuatro veces d�bil y etc.
Con esta ley del inadecuado crecimiento del volumen y peso de un animal, adem�s del esfuerzo muscular se explican, porque un insecto, como una hormiga, abeja, etc. pueden subir cargas 30 � 40 veces mayor del peso de su cuerpo, cuando una persona normal es capaz de subir solamente 9/10, y el caballo, 7/10 de su peso.�
Despu�s de las explicaciones vamos a mirar las hazañas de hormigas "gigantes" desde otro punto de vista. Como el fabulista Y. A. Krylov burlonamente escribe:
|
Una hormiga tiene una fuerza excelente,
De cual no lo conoce la antigüedad; Y adem�s (le dice su fuente viejo) Podr�a levantar dos grandes granos de cebada. |
Volver