GEOMETRIA RECREATIVA
PARTE PRIMERA
GEOMETRIA AL AIRE LIBRE

Contenido:
1. Medir la anchura de un r�o.
2. Con ayuda de una visera.
3. Longitud de la isla.
4. Un peat�n al otro lado.
5. Los tel�metros m�s ordinarios.
6. La energ�a de los r�os.
7. La velocidad de la corriente.
8. Cu�nta agua pasa por el r�o.
9. La rueda de agua.
10. La placa irisada.
11. Los c�rculos en el agua.
12. Un ob�s fant�stico.
13. La ola de quilla.
14. La velocidad de los proyectiles.
15. La profundidad de un estanque.
16. El cielo estrellado en el r�o.
17. Un camino a trav�s del r�o.
18. Construir dos puentes.



1. Medir la anchura de un r�o.
Sin atravesando el r�o nadando, medir su anchura es tan f�cil, para quien conoce la geometr�a, como determinar la altura de un �rbol sin subir encima. Una distancia inaccesible mide a trav�s de los modos, anteriormente descriptos, como la medici�n de la altura inaccesible. En ambos casos un trayecto buscado lo substituimos con la otra medida, la cual es f�cil de medir inmediato.
Entre los muchos modos de solucionar esta Problema, distinguimos algunos m�s sencillos.
1.� Para el primero necesitamos un "aparato" ya conocido por nosotros, como tres alfileres sobre los v�rtices del tri�ngulo rect�ngulo is�sceles (Figura 25).
Necesitamos encontrar la anchura AB de r�o (Figura 26), estando en aquella orilla, donde se encuentra el punto B , y sin atravesar al otro lado. Estando sobre el punto C, mantenga el aparato cerca de los ojos as�, cuando mira con un solo ojo a trav�s de dos alfileres, se ve como ambos est�n tapando los puntos B y A .

Figura 25. Medici�n de la anchura de un r�o con el aparato de alfileres

Esta claro que cuando conseguimos esto, nos encontraremos justo en la prolongaci�n de la l�nea AB. Ahora, sin mover la tablilla, mire a lo largo de los otros dos alfileres (perpendicular a la direcci�n anterior) y fijemos un punto D , tapado con estos dos alfileres, es decir est� situado en la recta, perpendicular a AC.

Figura 26. La primera posici�n del aparato de los alfileres.

Despu�s clavamos un jal�n en el punto C, dejamos este sitio y nos instalamos con el instrumento a lo largo de la recta CD, hasta que no encontraremos un punto E sobre ella (Figura 27), de donde es posible al mismo tiempo alinear el alfiler b con la p�rtiga del punto C , y el alfiler a, con el punto A.

Figura 27. La segunda posici�n del aparato de los alfileres.

Esto significa que hemos encontrado el tercer v�rtice del tri�ngulo ACE , sobre la orilla, donde el �ngulo C es recto, el �ngulo E es igual al �ngulo agudo del aparato de los alfileres, es decir � del �ngulo recto. Evidentemente que el �ngulo A es igual a un �ngulo recto, es decir
AC = CE.
Si medimos la distancia CE a trav�s de los pasos, encontraremos la distancia AC, y quitando BC, el que es f�cil de medir, encontraremos la anchura buscada de r�o.
Es bastante inc�modo y dif�cil tener en la mano el aparato sin moverlo; mejor fijar la tablilla sobre un palo con una punta para mantener verticalmente sobre la tierra.

Figura 28. Utilizando las propiedades de igualdad a los tri�ngulos.

2.� El segundo modo es parecido al primero. Aqu� tambi�n se encuentra un punto C a lo largo de AB y se marca con ayuda del aparato de los alfileres la l�nea recta CD bajo �ngulo recto sobre el CA. Pero despu�s se act�a de otra manera (Figura 28). Sobre la l�nea recta CD se medir� dos distancias arbitrariamente iguales CE y EF y marcamos los puntos E y F con sendos jalones.
Despu�s estado con el aparato en el punto F, marcamos la direcci�n FG, perpendicular sobre el FC . Ahora vamos a andando a lo largo de la FG, buscando sobre la l�nea el punto H , desde el cual el jal�n E parece que est� tapando al punto A. Esto significa, que los puntos H, E y A encuentran sobre una l�nea recta.
La Problema esta solucionada: la distancia FH es igual a la distancia AC, desde cual es suficiente quitar BC, para encontrar la anchura buscada de r�o ( los lectores, evidentemente, adivinen el mismo, porque FH es igual a AC ).
Este modo necesita m�s sitio que el anterior; si un lugar lo permite hacer de ambos modos, es �til comprobar un resultado con el otro.

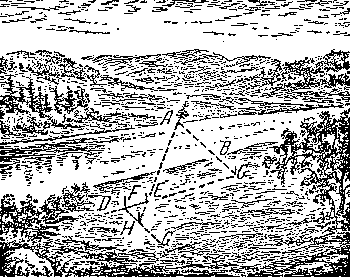
3.� En el modo ahora descrito, es una modificaci�n del anterior: medir sobre la l�nea CF distancias no iguales, donde una es tantas veces menor que la otra.

Figura 29. Utilizando las propiedades de semejanza a los tri�ngulos.

Por ejemplo (Figura 29), hacemos FE cuatro veces menor que EC, despu�s actuamos como siempre: a la direcci�n FG, perpendicular sobre FC, se busca el punto A. Pero ahora FH no es igual a AC, es menos de esta distancia en cuatro veces: el tri�ngulo ACE y EFH aqu� no son iguales, son semejantes (tienen los �ngulos iguales sobre los lados no iguales). De la semejanza de los tri�ngulos tenemos la proporci�n

AC : FH = CE : EF = 4 : 1.
Entonces, midiendo FH y multiplicando el resultado por 4, obtenemos la distancia AC, y quitando BC, encontraremos la anchura buscada de r�o.
El modo, como podemos comparar, no necesita mucho sitio y por eso es c�modo para llevar a la pr�ctica.
4.� El modo cuarto b�sicamente es utilizando las propiedades del tri�ngulo rect�ngulo, cuando uno de los �ngulos agudos es 30�, entonces el cateto inverso equivale a la mitad de la hipotenusa.

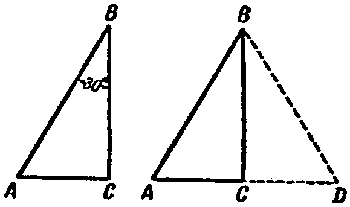Figura 30. Cuando el cateto es igual a la mitad de la hipotenusa

Asegurarse que la posici�n es exacta es muy f�cil: sea que el �ngulo B del tri�ngulo rect�ngulo ABC (Figura 30, a la izquierda) es 30�; demostraremos que en este caso
AC = � AB.
Hacemos girar el tri�ngulo ABC sobre BC, quedando sim�tricamente ubicado con respecto a su postura anterior (Figura 30, a la derecha), creando una figura ABD; la l�nea ACD es recta, por que ambos �ngulos sobre el punto C, son rectos.
En el tri�ngulo ABD el �ngulo A = 60�, el �ngulo ABD, como est� formado con dos �ngulos de 30� tambi�n es 60�.
Entonces, AD = BD como dos lados estando frente a los �ngulos iguales. Pero AC = � AD; es decir, AC = � AB.
Deseando a utilizar esta caracter�stica de tri�ngulo, necesitamos colocar los alfileres encima de tablilla formando un tri�ngulo rect�ngulo, donde el cateto es la mitad de la hipotenusa.
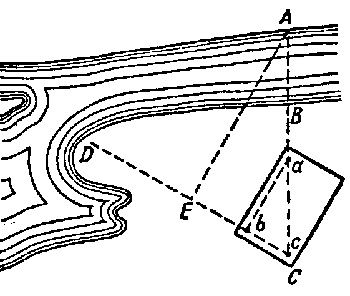
Con este instrumento se ubica en un punto C (Figura 31) As�, con la recta AC coincide con la hipotenusa de tri�ngulo de los alfileres.

Figura 31. Esquema del uso el tri�ngulo rect�ngulo con un �ngulo de 30�

Mirando a lo largo del cateto corto de este tri�ngulo, marcamos la direcci�n CD y sobre cual encontraremos un punto E, donde EA es perpendicular a CD (lo construimos con la ayuda del mismo aparato de los alfileres). Es f�cil de comprender, que la distancia CE, cateto enfrente al �ngulo de 30�, es igual a la mitad de AC. Entonces midiendo CE, doblando esta distancia y rest�ndole BC, tenemos la anchura buscada AB de r�o.
As� son los cuatro modos f�ciles de utilizar, con ayuda de los cuales siempre es posible, sin atravesar el r�o, medir la anchura del mismo con resultado plenamente satisfactorio. No vamos a examinar los modos dif�ciles, los que necesitan aparatos especiales para hacer las mediciones.
Volver

2.- Con ayuda de una visera .
Un modo, que fue muy �til para el coronel mayor Kuprianov, estando en una situaci�n de guerra. Le mandaron medir la anchura de un r�o, a trav�s de cual necesitaba organizar un pasaje�
�Acerc�ndose furtivamente la subdivisi�n de Kuprianov hasta el arbusto al lado de r�o, se escondieron, pero �l junto con el ayudante Karpov salieron a poca distancia del r�o, de donde se ve muy bien a la orilla enfrente, donde se escondi� el enemigo. En estas condiciones necesitaba medir la anchura, confiando a su vista.
��A ver, Karpov, cu�nto mide el ancho del r�o? � pregunt� Kuprianov.
�Penso, no m�s que 100 a 110 metros, - se respondi� el Karpov.
�El coronel estuvo de acuerdo con su ayudante, pero para la seguridad decidi� medir la anchura de r�o con ayuda de su "visera".

Figura 32. Por debajo de una visera deberemos notar un punto en la orilla apuesta.

�El modo es el siguiente. Necesita ponerse enfrente al r�o y calar la gorra sobre los ojos as�, para poder ver justo bajo de la visera la l�nea de orilla opuesta (Figura 32).
�La visera la podemos substituir con la palma de la mano o con una agenda, situando el canto en la frente. Despu�s sin cambiar de posici�n la cabeza, gira a la izquierda o a la derecha, o atr�s (en aquella parte, donde el campo es m�s llano, accesible para medir la distancia) y observamos el punto m�s lejano, visible bajo de la visera ( de la palma o de la agenda).
�La distancia hasta este punto es la anchura del r�o aproximadamente.
�Este es el modo que utiliza el coronel. R�pidamente se levant�, llev� la agenda al frente, r�pidamente dio la vuelta y ubic� el punto lejano. Despu�s �l con el ayudante Karpov, arrastr�ndose llegaron hasta el punto, midiendo la distancia con una cuerda. El resultado fue 105 metros.
Kuprianov dej� el resultado a sus ayudantes.�

Problema
Dar la explicaci�n geom�trica al modo de la "visera".

Figura 33. Sobre el mismo modo, marcar el punto en la orilla donde estamos

Soluci�n
El rayo de la vista, tocando el borde de la visera ( palma o agenda), es primero apuntado a la l�nea de la orilla apuesta ( Figura 32). Cuando la persona da vuelta, pues el rayo de vista, lo mismo que la pata de comp�s, describe la circunferencia, entonces AC = AB , como los radios de la circunferencia (Figura 33).
Volver

3. Longitud de la isla.
Problema
Ahora tenemos un problema m�s dif�cil. Estando en la orilla de un r�o o de un lago, vemos una isla (Figura 34), cuya longitud deseamos conocer sin dejar la orilla, por supuesto. �Es posible hacer la medici�n?

Figura 34. Como encontrar la longitud de una isla.

Aunque en este caso para nosotros ambos extremos de la l�nea medida, son inaccesibles. La Problema se solucionara, adem�s sin aparatos especiales.

Soluci�n
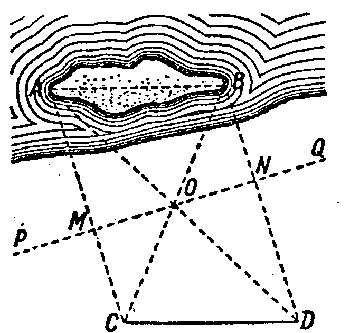
Necesitamos saber la longitud AB (Figura 35) de la isla, permaneciendo en la orilla durante la medici�n.

Figura 35. Utilizando las propiedades de igualdad de los tri�ngulos rect�ngulos

Eligiendo dos puntos P y Q arbitrarios, se marcan con jalones y se buscan sobre la recta PQ los puntos M y N as�, cuando los sentidos AM y BN formaban con la direcci�n PQ, �ngulos rectos (para esto utilizaremos el aparato de los alfileres).
En el centro O del trazo MN se marca con otro jal�n y se busca a lo largo de la l�nea AM el punto C, donde el jal�n O parece que est� tapando el punto B. Igualmente a lo largo de la BN buscan el punto D, donde el jal�n O parece esta tapando el extremo A de la isla. La distancia CD es la longitud buscada.
Demostrar esto no es dif�cil.
Cogemos dos tri�ngulos rect�ngulos AMO y OND ; sus catetos MO y NO son iguales, adem�s los �ngulos AOM y NOD son iguales, entonces, los tri�ngulos son iguales entre s�, y

AO = OD.
De igual manera podemos deducir que

BO = OC.
Comprobando despu�s los tri�ngulos ABO y COD, deducimos que

AB = CD.
Volver

4. Un peat�n al otro lado.
Problema
A lo largo de un r�o est� paseando una persona. Al otro lado Ud. precisamente distingue sus pasos. �Podemos, sin movernos, encontrar la distancia aproximada entre el peat�n y Ud., sin tener ning�n instrumento a mano?

Soluci�n
No tenemos ning�n aparato, pero hay ojos y manos, y eso es suficiente. Estiraremos la mano hacia el peat�n y miramos al fin del dedo con un solo ojo, el derecho si el peat�n esta andando a mano derecha, el izquierdo, si el peat�n esta andando a mano izquierda.

Figura 36. Como encontrar la distancia hasta el peat�n, andado por la orilla apuesta.

Inmediatamente que el dedo tapa al peat�n (Figura 36), cierre el ojo con el cual observan, y abren el otro: el peat�n aparece alejado un poco hacia atr�s. Contaremos, cuantos pasos hacia delante �l da, antes que se junte otra vez con el dedo. Ahora tenemos todos los datos necesarios para tener un resultado aproximadamente.
Explicaremos c�mo utilizar estos datos. En la Figura 36, sean a b nuestros ojos; el punto M, fin del dedo de la mano estirada; el punto A, primera medici�n de la distancia al peat�n y B, la segunda.
Los tri�ngulos aBM y ABM, son semejantes (deberemos dar la vuelta hacia el peat�n cuando ab sea paralela a la direcci�n de su movimiento).Entonces,

BM ´ bM = AB ´ . ab
es la proporci�n, donde se desconoce el miembro BM, todo el resto lo podemos medir inmediatamente. Efectivamente, bM es la longitud de la mano; ab es la distancia entre las pupilas de ojos, AB lo medido con los pasos de peat�n (el paso tomaremos � � metros ).
Por lo tanto, tenemos la distancia desconocido entre el observador y el peat�n en la orilla apuesta


Si, por ejemplo, la distancia entre las pupilas (ab) es de 6 cent�metros, la longitud bM desde el fin de mano hasta los ojos, 60 cent�metros, y el peat�n hizo desde A hasta B, digamos, 14 pasos, entonces la distancia desde �l hasta el observador es

MB = 14 ´ 60 / 6 = 140 pasos, � 105 metros.
Es suficiente conocer la distancia entre las pupilas y bM, la distancia desde los ojos hasta el extremo de mano estirada, y recordar su proporci�n bM/ab, para encontrar r�pidamente la distancia a objetos inaccesibles. Solo falta multiplicar AB por la proporci�n. La mayor�a de las personas, tienen bM/ab m�s o menos igual a 10. La dificultad es encontrar, de cualquier manera, la distancia AB. En nuestro caso estamos utilizando los pasos de peat�n. Pero podemos utilizar otros datos tambi�n.
Si por ejemplo, necesitamos encontrar la distancia hasta el tren, entonces la longitud AB podemos tener comprobando con la longitud de un vag�n, el que conocemos ( 7,6 metros entre los topes). Si necesitamos buscar la distancia hasta la casa, entonces AB podr�a ser el ancho de una ventana o el tamaño de ladrillo, etc.
Este sistema lo podemos utilizar para determinar el tamaño de los objetos lejanos, si sabemos la distancia hasta el observador.
Probaremos utilizar diferentes "tel�metros", los cuales describimos enseguida.
Volver

5. Los tel�metros m�s ordinarios.
Anteriormente, en el capitulo primero, hemos descrito un aparato bastante sencillo para medir las alturas, el alt�metro. Ahora describimos un instrumento, para medir distancias inaccesibles y se llama tel�metro. Un tel�metro muy ordinario lo podemos preparar de una cerilla. Unicamente suficiente marcar las divisiones milim�tricas, blancas y negras, uno a trav�s de otro (Figura 37).

Figura 37. Cerilla � tel�metro

Imaginaremos, los vemos a lo lejos una persona y formaremos una problema, encontrar la distancia hasta �l.
En este caso la cerilla � tel�metro es muy �til. Manteniendo en la mano estirada y mirando con solo un ojo, llevaremos su extremo a coincidir con la parte superior de la persona.

Figura 38.

Despu�s, despacio movemos la uña del dedo pulgar sobre la cerilla, fijando el punto donde se proyectan los pies de la persona. Los queda por saber, acercando la cerilla, sobre qu� divisi�n se fij� la uña, y ya tenemos los datos para resolver el problema.
Es f�cil de asegurarse que la proporci�n es correcta:


Desde este momento ya no es dif�cil calcular la distancia buscada. Si, por ejemplo, la distancia hasta la cerilla es 60 cent�metros, la estatura de una persona es 1,7 metros, y la parte medida de cerilla es 12 mil�metros, entonces la distancia es:


Llevando a la pr�ctica, para tener un mejor conocimiento, utilizando este tel�metro podemos medir la estatura de un amigo, o proponiendo alejarse, encontrar en cuantos pasos �l se alej� del observador.
Con el mismo modo podemos encontrar la distancia hasta el jinete (la altura mediana es 2,2 metros ), hasta la bicicleta (el di�metro de rueda es 75 cent�metros ), hasta el poste telegr�fico a lo largo de ferrocarril (la altura es 8 metros, la distancia entre los aisladores son 90 cent�metros ), hasta el tren, la casa y etc. las medidas de los que no es dif�cil de encontrar. Durante una excursi�n podemos utilizar el modo tambi�n.
Podemos hacer a mano un aparato muy c�modo del mismo tipo, el que sirve para encontrar la distancia a trav�s de la altura de una persona que est� lejos.
El instrumento los podemos ver en las figuras 39 y 40.
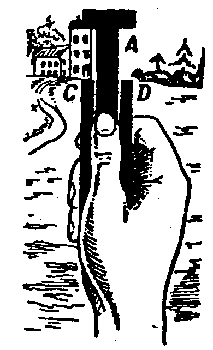
El objeto observado coloca en el espacio A, el que se alinea con la parte alta de instrumento.
El tamaño del espacio se determina por las divisiones en las partes C y D de tablilla. Para librarse de la necesidad de hacer los c�lculos, podemos en la parte C señalizar, enfrente las divisiones, las distancias correspondientes a ellos, si el objeto observado es la figura de una persona (mantenga el instrumento enfrente los ojos con la mano estirada).

Figura 39.

En la parte derecha D puede señalizar las distancias, calculadas antes para cualquier necesidad, cuando se observa la figura del jinete ( 2,2 cent�metros ). Para el poste telegr�fico (altura � 8 metros ), el aeroplano con alas es 15 metros y para otros objetos podemos utilizar la parte libre de los C y D . Al final, nuestro instrumento va a tener un aspecto presentado en la Figura 40.

Figura 40. La estructura del tel�metro sobresalido

Evidentemente, la distancia as� determinada es siempre exacta. El ejemplo que examinamos anteriormente, donde la distancia hasta la persona fue valorada en 85 metros , un error en solo 1 mil�metro durante la medici�n con la cerilla da una equivocaci�n de resultado en 7 metros (1/12 de 85).
Pero si la persona estuviera en cuatro veces m�s lejos, medimos con la cerilla no 12, si no 3 mil�metros, entonces el error ser� solamente en � mil�metro se cambia el resultado en 57 metros. Por eso, nuestro ejemplo es seguro �nicamente para distancias m�s cercanas, 100 a 200 metros. Para las distancias m�s largas tenemos que buscar los objetos m�s grandes.
Volver

6. La energ�a de los r�os.
Un r�o cuya longitud no es m�s que 100 kil�metros , tomamos como pequeño. �Sabe cu�ntos r�os as� hay en nuestro pa�s? �Muchos, 43.000 !
Si pusi�ramos todos los r�os en una l�nea, tendr�n una cinta de longitud 1.300.000 kil�metros. Con esta cinta podemos ceñir el globo terrestre treinta veces sobre el ecuador (la longitud ecuatorial es 40 000 kil�metros).
La corriente de agua de un r�o se mueve lentamente, pero �l mantiene en secreto una reserva de energ�a inagotable. Especialistas est�n pensando, si fuera practicable sumar las posibilidades ocultas de todos los r�os pequeños, los que corren por nuestras tierras, �recibimos una cantidad considerable de 43 millones de kilovatios ! Esta energ�a gratis deber�a ser utilizada para la electrificaci�n econ�micas de las localidades situadas cerca de los r�os.
Sabemos que la realizaci�n es posible con la ayuda de las centrales hidroel�ctricas y todos pueden demostrar iniciativa y ayuda real sobre la preparaci�n y la construcci�n de una central. La verdad, a los constructores les interesa todo, a qu� sistema pertenece el r�o: su anchura y velocidad de corriente ("consumo de agua"), la superficie del corte transversal del lecho ("corte vivo") y cual es la presi�n de agua bajo las orillas. Todo esto es posible de medir con los medios a mano y aqu� mismo presentamos una Problema geom�trica, pero no muy complicada.
Ahora empezaremos a solucionar esta Problema.
Pero antes tienen que conocer algunos consejos pr�cticos de parte los especialistas ingenieros V. Yaros y I. Fiodorov. Como elegir el sitio para construcci�n futura.
�"Una central no grande, ellos recomiendan construir no m�s cerca de 10 a 15 kil�metros y no m�s lejos que 20 a 40 kil�metros desde la fuente de r�o, porque el alejamiento trae consigo el encarecimiento de la presa y abre gran afluencia de agua. Si se construye la presa m�s cerca que 10 a 15 kil�metros desde la fuente, la central hidroel�ctrica, por la pequeña afluencia de agua y sin la presi�n suficiente, no puede proveer a la potencia necesaria. La parte elegida de r�o no debe de ser de gran profundidad, ya que aumenta el valor de la construcci�n, necesitando un fundamento muy pesado".�
Volver

7. La velocidad de la corriente.
�Cuanta agua corre durante el periodo de veinticuatro horas en este sitio?
El c�lculo no es dif�cil: La medici�n la realizan dos personas. Uno con un reloj en la mano y el otro con la boya o, por ejemplo, con una botella bien cerrada con una banderilla. Eligen un trozo de r�o rectil�neo y colocan a lo largo de r�o dos jalones A y B a la distancia 10 metros uno del otro. (Figura 41).
Sobre las l�neas, perpendiculares al AB, colocan otros m�s jalones C y D. Uno de los observadores con el reloj esta detr�s del jal�n D. El otro, con la boya va hacia arriba del jal�n A, tira la boya al agua, y se pone detr�s del jal�n C. Ambos miren a lo largo de sentidos CA y DB sobre la superficie de agua. En el momento, cuando la boya est� cruzando la prolongaci�n de la l�nea CA, el primero observador levanta la mano. Con esta señal el otro observador empieza a medir el tiempo y detiene la medici�n cuando la boya cruza la l�nea DB.
Por ejemplo, supongamos que la diferencia de tiempo fue de 20 segundos.
Entonces, la velocidad de corriente del r�o:

10 / 20 = 0,5 metros / segundo.
Usualmente, las mediciones se repiten un par de veces, tirando la boya en puntos diferentes de la superficie de r�o. Despu�s suman las velocidades obtenidas y se dividen en la cantidad de medidas. Esto determina la velocidad media que lleva la superficie del r�o.
Las capas m�s profundas corren m�s despacio, y la velocidad mediana de todo el torrente es como 4/5 de la velocidad superficial, en nuestro caso, entonces, 0,4 metros / segundo.
Podemos encontrar la velocidad superficial con otro modo, pero menos seguro.

Figura 41. La medici�n de la velocidad al corriente de un r�o

Montamos una lancha y flotamos un kilometro (marcado en la orilla) contra la corriente, despu�s volverse e irse con la corriente, remando con la misma fuerza.
Supongamos que recorremos los 1000 metros contra la corriente en 18 minutos, y a favor de la corriente, en 6 minutos. Designando la velocidad buscada del r�o a trav�s de x, la velocidad de nuestro movimiento en el agua estancada a trav�s de y , formemos una ecuaci�n


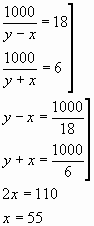
La velocidad de agua corriente sobre la superficie es 55 metros / segundo, es decir, la velocidad media ser� cerca de 5/6 metros /segundo .
Volver

8. Cu�nta agua pasa por el r�o.
De una manera u otra siempre es posible encontrar la velocidad de la corriente de un r�o. Un poco complicada es la otra parte de la preparaci�n necesaria para calcular la cantidad del agua corriente, encontrar la superficie del corte transversal del agua. Para saber la superficie, "el corte vivo" del r�o necesariamente hay que preparar el plano de aquel corte.
El levantamiento del corte vivo es el siguiente:

Primer m�todo
En el mismo sitio, donde los medimos la anchura del r�o, junto al agua, en ambas orillas, clavamos dos jalones. Despu�s con un amigo montamos una lancha y vamos desde un jal�n hasta el otro, todo el tiempo siguiendo exactamente una l�nea recta, la que une los dos jalones. El amigo debe de ser un buen remero; adem�s, �l debe ser ayudado por un tercer miembro de trabajo, que estando en la orilla, observa, para que la lancha siga bien su direcci�n, y en los casos necesarios dar unos señales al remero, hacia d�nde deber�a girar.
En el primer pasaje por el r�o deberemos contar solamente, cual es la cantidad de los golpes con los remos �l necesitaba, y desde aqu� saber, cual es la cantidad de los golpes necesaria para trasladar la lancha en unos 5 o 10 metros.
Cuando hacemos la segunda navegaci�n, pero ahora con un list�n apropiado para medir, y cada 5 � 10 metros (medidos mediante la cantidad de los golpes de remo) se hunde el list�n en el agua verticalmente hasta el fondo del r�o, anotando la profundidad de r�o en este sitio.
En esta forma podemos medir el "corte vivo" del r�o, si no es muy grande; para un r�o muy ancho, con mucha agua, se necesitan unos modos m�s dif�ciles. Este trabajo lo dejaremos para los especialistas. Los aficionados eligen las Problemas, correspondientes a sus sencillos recursos.

Segundo m�todo.
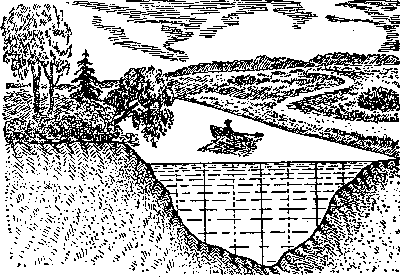
Para un r�o estrecho y poco profundo no necesitamos una lancha. Entre los jalones se estira perpendicularmente a la corriente, una cuerda con nudos hechos cada 1 metro , y bajando el list�n sobre el cada nudo hasta el fondo, medimos la profundidad del cauce.

Figura 42. El "corte vivo" del r�o

Cuando todas las medidas est�n hechas, anotamos en el papel cuadriculado el plan del corte transversal. Obtenemos una figura, m�s o menos, como vemos en la Figura 42. Ahora podemos encontrar su superficie, como ella esta dividida en numerosos trapecios (donde conocemos las bases y las alturas) y por dos tri�ngulos extremos tambi�n con la base y la altura conocida. Si, la escala del plano es 1 : 100, entonces, el resultado lo obtenemos en metros cuadrados.
Ahora tenemos los todos datos para calcular la cantidad de agua corriente. Evidentemente, a trav�s del corte vivo corre un volumen de agua en cada un segundo, igual al volumen de un prisma, donde la base es el corte, y la altura, la velocidad media de la corriente.
Si, por ejemplo, la velocidad media de la corriente en el r�o es 0,4 metros /segundo, y la superficie del corte vivo, digamos, es 3,5 metros cuadrados, entonces incesantemente cruzan a trav�s del corte:

3,5 � 0,4 = 1,4 metros c�bicos de agua por segundo, o 1,4 toneladas ( 1 m ³ de agua potable pesa 1 tonelada = 1000 kilogramos).
En una hora: 1,4 � 3 600 = 5 040 m ³
En el periodo de veinticuatro horas: 5 040 � 24 = 120 960 m ³ �m�s de cien mil metros c�bicos!

Figura 43. Estaci�n hidr�ulica con potencia de 80 kilovatios de una artel agr�cola de Burmakin; da energ�a para los siete koljoces.

En tal caso el r�o con el corte vivo de 3,5 metros ² es un r�o pequeño: �l puede tener, digamos, 3,5 metros de anchura y de 1 metro de profundidad, es posible de vadear, pero �l tiene guardada mucha energ�a capaz de convertirse en electricidad. �Cu�nta agua corre durante el periodo de veinticuatro horas por un r�o como el Neva, si a trav�s de su corte vivo pasan 3.300 metros ³ de agua?
Es el "consumo medio" de agua en el Neva de San Petersburgo. "El consumo medio" de agua en el Dnepro de Kyev es de 700 metros ³ .

Figura 44. La medici�n del corte vertical de las orillas

Los prospectores j�venes y los constructores futuros de su central hidroel�ctrica necesitan saber cual es la presi�n de agua sobre las orillas de r�o, es decir, cual diferencia de niveles podr�a formar la presa (Figura 43).
Por eso en 5 a 10 metros de las orillas del agua en colocan dos estacas, habitualmente sobre la l�nea perpendicular al corriente del r�o. Pasando despu�s sobre esta l�nea, se ponen pequeños piquetes en los sitios de la fractura litoral (Figura 44). Con ayuda de las reglas se mide la sobresaliente a uno sobre el otro piquete y la distancia entre ellos.
Con los datos de medici�n se hace el plano del perfil del litoral anal�gicamente al dibujo del perfil de cauce.
Por el perfil del litoral podemos calcular magnitud de la presi�n.
Supongamos que la presa sube el nivel de agua hasta 2,5 metros. En este caso podemos calcular la potencia posible de la central hidroel�ctrica.
Para esto los ingenieros electricistas nos recomiendan multiplicar 1,4 ("consumo" del r�o por segundo) por 2,5 (la altura del nivel de agua) y por 6 (el coeficiente dependiente de la p�rdida de energ�a en las maquinas). El resultado tenemos en kilovoltio. Entonces,

1,4 � 2,5 � 6 = 21 kilovoltio.
Como los niveles del r�o cambian a lo largo del año, el consumo tambi�n lo hace, para el c�lculo tenemos que saber el valor t�pico de consumo de agua anual.
Volver

9. La rueda de agua.
Problema
La rueda provista de paletas se instala en el fondo del r�o (Figura 45). �C�mo va girar la rueda, si la corriente toma la direcci�n hacia la izquierda?


Soluci�n
La rueda se gira contra el reloj. La velocidad de la corriente de las capas m�s profundas es menor que la velocidad de las capas superiores de la corriente, entonces, la presi�n sobre las paletas de arriba sea mayor, que la de abajo.
Volver

10. La placa irisada.
En un r�o, donde baja el agua desde una f�brica, podemos observar las manchas coloradas. Aceite, bajando al r�o junto con agua de la f�brica, deja en la superficie del r�o estas manchas ligeras. �Podemos saber, aproximadamente, la anchura de una de estas placas?
La Problema parece complicada, pero soluci�n no es tan dif�cil. Noten que nosotros no vamos a medir la anchura de la placa ahora mismo. La calcularemos de manera indirecta.
Cogemos una cantidad de aceite mec�nico, por ejemplo, 20 gr y lo echamos al agua, lejos de la orilla, por supuesto. Cuando la placa tome la forma de un c�rculo, medimos aproximadamente su di�metro. Sabiendo el di�metro, encontraremos la superficie. Y como sabemos el volumen (se calcula por el peso), entonces no ser� dif�cil encontrar la anchura buscada de la placa. Miraremos atentamente el ejemplo.

Figura 45. �El que sentido tome la rueda?

Problema
Un solo gramo de petr�leo, est� formando una charca de 30 cent�metros di�metro . �Cu�l es la anchura de la placa petrolera encima de agua? Un cent�metro cubico del petr�leo pesa 0,8 gr.

Soluci�n
Encontraremos el volumen de la placa, el cual, evidentemente, es igual al volumen cogido de petr�leo. Si 1 cm ³ de petr�leo pesa 0,8 gr, entonces, para un gramo es 1/0,8 = 1,25 cm3 o 1.250 mm ³ . La superficie del c�rculo con el di�metro de 30 cent�metros, o 300 mil�metros, es 70.000 mm ² . La anchura buscada es igual al volumen, dividido por la superficie:


La medici�n directa con las medios habituales, evidentemente, no es posible.
Las placas que forman el aceite y el jab�n son las capas m�s finas, como 0,0001 mm y menos.
�"Una vez, cuenta el f�sico ingles Boyz en su libro "Pompas de jab�n", hice esta prueba en un estanque. En la superficie del agua echo una cucharada del aceite de oliva. Inmediatamente se ha convertido en una mancha grande, con el di�metro 20 a 30 metros.
�Como la mancha es mil veces mayor por su longitud y por su anchura sobre la cuchara, pues, la capa del aceite sobre agua tiene que ser, aproximadamente, una millon�sima parte de la anchura dentro de cuchara, o m�s o menos 0,000002 mil�metro. "�
Volver

11. Los c�rculos en el agua.
Problema
Mas de una vez, por curiosidad, miramos atentamente los c�rculos encima de agua estanca, formados al tirar a una piedra (Figura 46). No es dif�cil de explicar este fen�meno de la naturaleza: la agitaci�n extiende desde un punto principal en todas direcciones con la misma velocidad; por eso en cada momento todos los puntos perturbados se alejan la misma distancia del punto de aparici�n de la perturbaci�n, es decir, sobre la una circunferencia.

Figura 46. Los c�rculos sobre el agua

�Pero qu� pasa en el agua corriente? �Tienen las olas originadas por una piedra tirada, formar un c�rculo o su forma es alargada?
En primer lugar, parece que en el agua corriente las olas deber�an alargarse y tomar el sentido del r�o: la agitaci�n en el agua corriente es m�s r�pida, que en los sentidos laterales. Por eso, las partes excitadas de la superficie acu�tica, tienen que formar una l�nea curva larga y cerrada, pero, por ninguna manera forman la circunferencia.
En la realidad, no es as�. Tirando las piedras en una corriente del r�o muy r�pido, podemos asegurar que las olas son circulares, son las mismas como en aguas estancadas. �Por que?

Soluci�n
El motivo es siguiente. Si el agua no se mueve, las olas son circulares. �El que cambie viene con la corriente? La corriente lleva cada punto de esta ola en la direcci�n, marcada por las flechas (Figura 47, a la izquierda), adem�s, todos los puntos traspasan por las l�neas paralelas con la misma velocidad, es decir, sobre las mismas distancias.

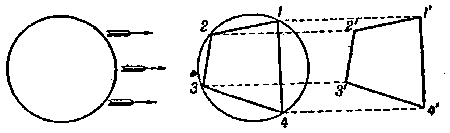
Figura 47. La corriente de agua no cambia la forma de las olas

"El traspaso paralelamente" no cambia la forma de una figura. Exactamente, al final de este traspaso el punto 1 (Figura 47, a la derecha) aparece un punto 1', el punto 2 en el punto 2', y etc.; el tetr�gono 1 2 3 4 se cambia por el tetr�gono 1' 2' 3' 4', los cuales son iguales, como podemos ver, toman las formas de los dos paralelogramos, 1 2 2' 1', 2 3 3' 2', 3 4 4' 3' y etc. Tomando en la circunferencia m�s de cuatro puntos, obtenemos pol�gonos iguales; por fin, cogiendo una cantidad de puntos infinita, entonces, obtenemos una circunferencia.
Por eso el movimiento del agua no cambia la forma de una ola, en el agua corriente ellas son c�rculos. La �nica diferencia es, que en la superficie de un estanco los c�rculos no se mueven (sin contar que ellos se divergen desde su centro); en la superficie de un r�o los c�rculos se mueven junto con su centro y con la misma velocidad de la corriente.
Volver

12. Un ob�s fant�stico.
Problema
Empezaremos con la Problema, la cual parece no tiene ninguna relaci�n con todo que estamos investigando, pero despu�s, como los veremos, va en el mismo sentido.
Imaginaremos una bomba de ob�s, volando hacia arriba; comienza a bajar y de repente se hay una explosi�n; los cascos de metralla vuelan por todos partes.
Los cascos son esparcidos con la misma fuerza que vuelan, sin encontrar ninguna resistencia en el aire. Pregunta: �Qu� destino forman los cascos pasado un segundo despu�s de la explosi�n, antes de llegar a la tierra?

Soluci�n
La Problema es semejante a la anterior, sobre los c�rculos en el agua. Pareciera que los cascos tienen que formar una figura, alargada hacia bajo, en el sentido de la ca�da; porque los cascos, lanzados hacia arriba, vuelan m�s despacio, que los lanzados hacia abajo.
No es dif�cil de demostrarlo, cuando los cascos de nuestra imaginada metralla tomen la forma de un globo. Imaginaremos en un segundo, que la gravitaci�n no lo existe; entonces, por supuesto, todos los cascos durante un segundo se alejan una determinada distancia desde su centro explosivo, es decir, forman la superficie del globo. Y si ahora incluimos la gravitaci�n, por su influencia los cascos deber�an bajar; y como sabemos, que todos los cuerpos bajan con la misma velocidad, entonces, los cascos durante en un segundo bajar�n la misma distancia, y adem�s, sobre las l�neas paralelas. Por eso es que mantiene la misma forma, la de globo.
As� es, los cascos del ob�s fant�stico deber�an formar un globo, el que parece hincharse, en la medida que bajan con la velocidad de la ca�da libre.
Volver

13. La ola de quilla .
Volvemos otra vez al r�o. Estado en un puente, atentamente miraremos en el rastro dejado por un barco. Vamos a ver como de la proa se separan, sobre el �ngulo, dos crestas de olas (Figura 48).
�Por qu� ellas aparecen? �Y por qu� el �ngulo entre ellas cuando es m�s agudo, m�s r�pido va el barco?
Para tener m�s claridad en la causa de la aparici�n las dos crestas, volvemos otra vez a los c�rculos divergentes en superficie acu�tica, aparecidos por los pedruscos tirados.
Tirando al agua los pedruscos con cierto intervalo, podemos observar en la superficie unos c�rculos de tamaños diferentes; adem�s el pedrusco tirado m�s tarde forma �l circulo m�s pequeño. Y si tiramos los pedruscos a lo largo de una l�nea recta, entonces, los c�rculos formados en su conjunto aparecer�n parecidos a las olas delante de la proa. Mientras m�s pequeño es el predusco tirado y mayor su frecuencia mayor ser� la semejanza. Hundiendo en el agua un palito y llev�ndolo sobre la superficie de agua, es como substituimos la ca�da los pedruscos irregulares por algo continuo y podemos reproducir la ola, la que vemos delante de la proa del barco.
Falta de añadir un poco para tener la claridad. Hundi�ndose en el agua, la proa del barco en cada segundo forma la misma ola circular, como la piedra tirada.

Figura 48. La ola de quilla

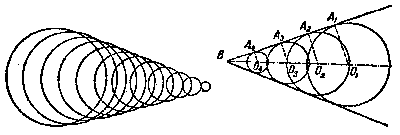
El circulo se aumenta, pero en este momento el barco tira para adelante y forma la otra ola circular, detr�s de cual viene tercera, y etc. La formaci�n irregular de los c�rculos, procedida por los pedruscos es substituida por su aparici�n continua, as� como podemos ver en la Figura 49.
Encontr�ndose las crestas de olas vecinas se rompen una a otra: intocables son aquellas dos partes de la circunferencia, los que est�n en sus partes exteriores. Uni�ndose, estas partes exteriores forman las dos crestas ininterrumpidas, teniendo la posici�n de los tangentes exteriores sobre todas olas circulares (Figura 49, a la derecha).

Figura 49. Como aparece la ola de quilla.

As� es como aparecen las crestas, las que los vemos detr�s del barco, y detr�s del cualquier cuerpo, movi�ndose sobre la superficie de agua.
De aqu� se ve, que este fen�meno es posible solamente cuando el cuerpo mueve m�s r�pido que las olas del agua. Si llevamos el palito sobre el agua lentamente, entonces, no podemos observar las crestas: Las olas circulares est�n situadas una entre otra y, entonces ser� imposible trazar la tangente com�n.
Las crestas divergentes las podemos observar en otro caso, cuando el agua corre frente a un cuerpo parado. Si, la corriente del r�o es bastante r�pida, entonces, las crestas aparecen en el agua, contorneando los pilares de un puente. Adem�s esta forma de olas se ve con m�s claridad, que aquellas que deja el barco, donde su forma no es perturbada por la acci�n de la h�lice.
Aclarada esta acci�n geom�trica, probamos a resolver otra Problema.

Problema
�De qu� depende la amplitud angular entre ambos ramas de la ola de quilla de un barco?

Soluci�n
Dibujaremos desde el centro de las olas circulares (Figura 49, a la derecha) los radios hasta las partes correspondientes de la cresta rectil�nea, es decir, hasta los puntos de la tangente general. Es f�cil de comprender, que el OB es el camino, dejado por el barco durante de un tiempo, y OA, la distancia, hasta el cual en mismo tiempo se extender�a la agitaci�n.
La proporci�n OA / OB, es el seno del �ngulo OBA , pero al mismo tiempo �sa es la proporci�n de las velocidades de la agitaci�n y el barco. Entonces, el �ngulo B entre la cresta, es como el doble �ngulo, del cual el seno es igual a la proporci�n de la velocidad corriente de las dos olas circulares sobre la velocidad del barco.
La magnitud de la velocidad de las olas circulares en el agua, m�s o menos es igual para todos los barcos; por eso el �ngulo de la divergencia de las ramas de la ola de la quilla depende, principalmente de la velocidad del barco: el seno de la mitad del �ngulo casi siempre es proporcional de esta velocidad. Y, al contrario, por el tamaño del �ngulo podemos determinar, en cuantas veces la velocidad del barco es mayor de la velocidad de las olas. Si, por ejemplo, el �ngulo entre los ramos de una ola de quilla es 30�, como para la mayor�a de los buques, entonces, el seno de su mitad ( seno 15�) es 0,26; es decir, la velocidad del barco es mayor que la de la corriente de las olas circulares en 1/0,26, es m�s o menos en cuatro veces.
Volver

14. La velocidad de los proyectiles.
Problema
Las olas, parecidas a las que acabamos de discutir, aparecen en el aire a trav�s de una bala disparada o de un proyectil de artiller�a.
Existen muchas maneras de hacer las fotos de un proyectil volando; en la Figura 50 son dos im�genes reproducidas por los proyectiles, circulando no con la misma rapidez. En ambos dibujos claramente podemos ver lo que nos interesada a nosotros "la ola de cabeza"(como se llaman a ella en estos casos).

Figura 50. La ola de la cabeza en el aire, creada por un proyectil volado.

Su aparici�n es parecida a la ola de quilla de un barco.
Y aqu� se utilizan las mismas proporciones geom�tricas: el seno de la mitad del �ngulo de la separaci�n de las olas de cabeza, es igual a la proporci�n de la velocidad de la agitaci�n sobre la velocidad del proyectil volado. Pero la agitaci�n en el aire se transmite con una velocidad, cerca de la velocidad de sonido, es 330 metros / segundo. Teniendo la foto de un proyectil volando, encontrar la aproximadamente su velocidad es f�cil. �C�mo podemos encontrar para estos dos im�genes?
Medimos el �ngulo de separaci�n de las dos ramas de la ola de cabeza en la Figura 50.
En primer caso tiene ~ 80�, en otro, ~ 55� . Mitad de ellos es 40� y 27�� .
El seno 40� = 0,64, seno 27�� = 0,46. Por lo tanto, la velocidad de agitaci�n de la ola de aire, es decir, 330m, es en el primer caso 0,64 de la velocidad del vuelo, y en el otro 0,46.
De aqu� se desprende la velocidad de primer proyectiles


y del segundo:


Como vemos, bastante simples razones geom�tricas, a parte de la ayuda de la f�sica, podemos resolver la Problema, a primera vista muy complicada: por una foto de un proyectil volando podemos encontrar su velocidad en el momento. (Este c�lculo es aproximado, por supuesto, porque no se han tenido en cuenta algunas circunstancias).
Problema
A quien desea, por su propia cuenta, hacer el calculo de la velocidad de unos n�cleos, aqu� lo tienen los tres im�genes de los proyectiles, volando con las velocidades distintas (Figura 51).

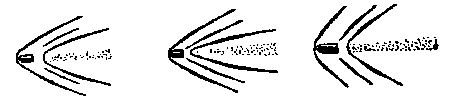Figura 51. �C�mo encontrar la velocidad de los proyectiles?

Volver

15. La profundidad de un estanque.
Los c�rculos sobre la superficie de agua nos desviaron la atenci�n hacia el asunto de la artiller�a. Volveremos otra vez junto al r�o y examinaremos una Problema hind� sobre una flor.
De viejos tiempos viene una tradici�n india, que es proponer una Problema en verso.

Problema

Sobre un lago tranquilo, Tamaño del medio pie, se levant� la flor de una maravilla. Creci� solita, sin familia. Y de repente vino aquel viento fuerte Que se llevo as�, para atr�s. No, no existe m�s flor, Pero no, la encontr� un pescador durante los d�as de primavera nueva A dos pies del sitio natal As� lo tengo la Problema: �Cu�l es del lago la profundidad?

Soluci�n
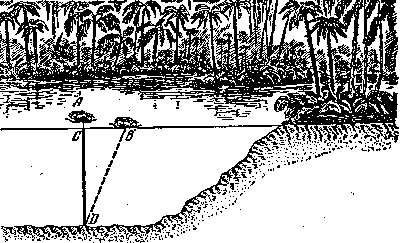
Indicaremos (Figura 52) la profundidad buscada CD del estanque a trav�s de x, despu�s sobre el teorema de Pit�goras, tenemos:

BD ² � x ² = BC ² ,

Es decir

Figura 52. La Problema india sobre la flor de loto

Cerca de la orilla de un r�o o de un estanque no muy profundo podemos encontrar una planta acu�tica, la que deja un material real para una Problema semejante: sin ning�n instrumento, sin mojarnos los pies y las manos, podemos encontrar la profundidad de un estanque en este sitio.
Volver

16. El cielo estrellado en el r�o.
El r�o por la noche tiene para nosotros una Problema. Recuerdo como Gogol tiene una descripci�n del Dnepro:
�"Las estrellas brillan encima del mundo y todas juntas se reflejan en el Dnepro.
A todas ellas tiene el Dnepro dentro de su seno: Ninguna puede escaparse, quiz�s, cuando se apague en el cielo."�
Es cierto, cuando est�s en la orilla de un r�o ancho parece que en el espejo acu�tico se refleja toda la c�pula de estrellas. �En realidad, es as�? �Todas los estrellas se "reflejan" en el r�o?
Haremos un plano (Figura 53):
A � el ojo del observador, estado en la orilla de r�o, cerca de lugar cortado al pico,
MN � es la superficie de agua.
�Cuales ser�n las estrellas que puede ver en agua el observador desde el punto A ?
Para contestar a esta pregunta, trazaremos desde el punto A una perpendicular AD hacia la recta MN y continuaremos en la misma direcci�n, hasta el punto A'. Si el ojo del observador est� en el punto A' , �l podr� ver solamente aquella parte del cielo, el cual esta dentro del �ngulo BA'C.
El campo visual es lo mismo mirando desde el punto A. Las estrellas que est�n fuera de este �ngulo, no puede ver; sus rayos reflejados pasan fuera del campo visual de sus ojos.

Figura 53. La parte del cielo estrellado que podemos ver estrellas en el agua

�C�mo podemos asegurarnos? �C�mo demostrar, que, por ejemplo, la estrella S , que est� fuera del �ngulo BA'C, no puede verla nuestro observador en el espejo de r�o? Sigamos detr�s de su rayo, cayendo cerca de la orilla en el punto M; el se refleja, de acuerdo a las leyes de la F�sica, en un �ngulo igual al �ngulo de incidencia SMP y, por lo tanto, menor del �ngulo PMA (es f�cil de demostrarlo aprovechando la igualdad de los tri�ngulos ADM y A'DM ); entonces, el rayo reflejado deber�a pasar de largo A. Adem�s pasar�n de largo de los ojos del observador los rayos de la estrella S, reflejadas en los puntos, situadas m�s distante del punto M.

Figura 54. En un r�o estrecho con las orillas bajas verlo en el espejo acu�tico de un r�o

Entonces, descripci�n de Gogol mantiene su vigencia: En el Dnepro no se reflejan todas estrellas, y tal vez menos de la mitad del cielo estrellado.
Adem�s, lo curioso es que gran extensi�n del cielo estrellado no es visto en un r�o ancho. En el r�o m�s estrecho y con las orillas bajas podemos observar casi la mitad de cielo(es decir, m�s que en un r�o grande), sin inclinarnos cerca de agua.
Es f�cil comprobar este asunto, haciendo la construcci�n de un campo visual. (Figura 54)
Volver

17. Un camino a trav�s del r�o.
Problema
Entre los puntos A y B pasa el r�o (o un canal) con las orillas m�s o menos paralelas (Figura 55) Necesitamos construir a trav�s del r�o un puente en �ngulo recto con sus orillas. �D�nde tenemos que elegir el sitio para el puente, para que el camino desde A hasta el B sea m�s corto?

Figura 55. Donde debemos construir el puente para que el camino sea m�s corto

Soluci�n
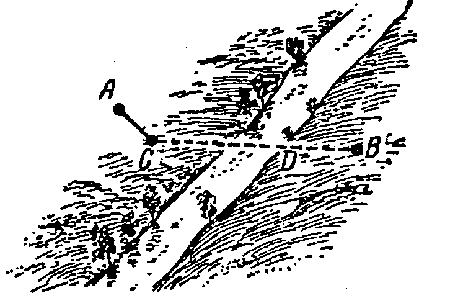
Pasando a trav�s del punto A (Figura 56) una l�nea recta, perpendicular hacia el sentido de r�o y marcar desde el A el segmento AC , igual a la anchura del r�o, unimos C con B. Despu�s en el punto D necesitamos construir el puente, para el camino desde el A hasta el B m�s corto.

Figura 56. El sitio elegido para la construcci�n esta bajo �ngulo recto sobre las orillas.

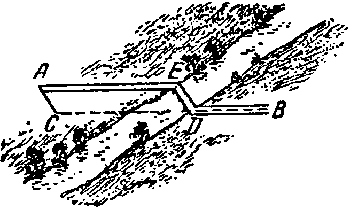
En realidad, construyendo el puente DE (Figura 57) y uniendo el E con el A, obtenemos el camino AEDB, donde la parte AE es paralela al CD ( AEDC, es paralelogramo, as�, como los lados enfrentados AC y ED son iguales y paralelos.) Por eso, el camino AEDB por su longitud es igual al camino ACB.
Es f�cil demostrar que el cualquier otro camino va ser m�s largo. Supongamos que existiera otro camino AMNB (Figura 58) m�s corto que AEDB, es decir, m�s corto que ACB. Uniendo C con N vemos que CN es igual AM. Entonces, el camino
AMNB = ACNM.
Pero CNB, evidentemente, es m�s que CB; entonces, ACNB es mayor que ACB, y por lo tanto, mayor que AECB. As� vemos que el camino AMNB no es m�s corto, es m�s largo que el camino AEDB.

Figura 57. El puente hab�a construido

Este razonamiento es aplicable a cualquier situaci�n del puente, si coincide con CD; o sea, el camino AEDB realmente es m�s corto.

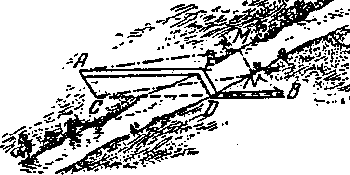
Figura 58. El camino AEDB � realmente es m�s corto

Volver

18. Construir dos puentes .
Problema
Probemos imaginar un caso m�s complicado, cuando necesitamos encontrar el camino m�s corto desde A hasta B a trav�s del r�o, pero ahora cruzando doblemente el r�o bajo �ngulo recto sobre las orillas (Figura 59) �En que sitios tenemos que construir los puentes?

Soluci�n
Deberemos desde el punto A (Figura 59, a la derecha) trazamos el segmento AC, igual a la anchura del r�o en la primera parte y perpendicular a sus orillas. Desde el punto B se pasa el segmento BO , igual a la anchura del r�o en la segunda parte y tambi�n perpendicular a las orillas. Unir los puntos C y D . En el punto E se construye el puente ED, en el punto G, el puente GH. El camino AFEGHB es el camino buscado m�s corto desde el A hasta el B.

Figura 59. Los dos puentes construidos

Como puede ver el lector, se razona en forma semejante al ejemplo anterior.
Volver