GEOMETR�A RECREATIVA
SEGUNDA PARTE
ENTRE PASO Y BROMA EN GEOMETR�A




CAPITULO NOVENO
LO ANTIGUO Y NUEVO SOBRE EL CIRCULO

Contenido:
1. Geometr�a practica de los egipcios y romanos
2. "Lo s� y recuerdo perfectamente"
3. El error de Jack London
4. Lanzamiento de aguja
5. Enderezamiento de circunferencia
6. Cuadratura del c�rculo
7. Tri�ngulo de Bingo
8. La cabeza y los pies
9. Alambre a lo largo de ecuador
10. Acci�n y calculo
11. Chica encima de una cuerda
12. Un vuelo a trav�s del Polo
13. Longitud de la correa de transmisi�n
14. Una tarea sobre la corneja prudente



1. Geometr�a practica de los egipcios y romanos
Cualquier alumno sabe calcular la longitud de una circunferencia dividida por el di�metro, mucho m�s exacto que un sacerdote de Egipto o un arquitecto de gran Roma. Los egipcios pensaban, que la circunferencia era mas larga que su di�metro en 3,16 veces, los romanos en 3,12, pero la proporci�n correcta es 3,14159� Los matem�ticos egipcios y romanos calcularon la proporci�n de la longitud sobre su radio, no de un modo geom�trico, sino que emp�ricamente. �Pero por qu� ellos tuvieron estos errores? �No pudieron ce�ir a un objeto redondo un hilo y luego, enderezarlo y simplemente medir?
Sin duda que ellos actuaron de esta manera; Pero no tenemos que pensar, que este modo da un buen resultado. Imaginen, por ejemplo, un jarr�n con el fondo redondo y el di�metro de 100 mm. Longitud de circunferencia tiene que ser 314 mm. Pero en la pr�ctica, midiendo con hilo, no obtendremos esta longitud: Simplemente un error de un mil�metro, y luego p ser�a equivalente a 3,13 o 3,15. Adem�s teniendo en cuenta la imposibilidad de medir di�metro de un modo exacto, los errores son inevitables, entonces el valor de p oscila entre


es decir, en fracciones decimales entre

3,09 y 3,18.
Uds. ven, que buscando p por el modo dicho, podemos recibir el resultado, no coincidiendo al 3,14: Una vez 3,1, segunda vez 3,12, tercera 3,17 y etc. Causalmente entre ellos aparece el 3,14, pero para contador este numero no tendr� gran significaci�n.
Este camino experimental no pudo dar un resultado aceptable para p . Entonces est� claro por qu� el mundo antiguo no sabia la proporci�n correcta de la longitud de circunferencia sobre su di�metro, y necesitaban un genio llamado Arqu�medes, para encontrar el valor de p = 3 1/7, sin medici�n, solamente reflexionando.
Volver

2. "Lo s� y recuerdo perfectamente"
En ,"Algebra" de un matem�tico �rabe Magamed � ben - Musa leemos sobre el c�lculo de la longitud de la circunferencia:
"La mejor manera es multiplicar el di�metro por 3 1/7 . Es el modo m�s f�cil y r�pido. El Dios sabe mejor."
Ahora sabemos, que el n�mero 3 1/7 del Arqu�medes no obstante exacto expresa la proporci�n de longitud de la circunferencia sobre di�metro. Te�ricamente no estaba demostrado, que esta proporci�n no puede ser expresada por una fracci�n. Nosotros podemos escribirla aproximadamente, a�n superando esta exactitud, respondiendo a las exigencias m�s estrictas de vida practica. Un matem�tico del siglo XVI Ludolf de Leuden, tuvo gran paciencia para calcular el n�mero con 35 decimales y su testimonio era grabar encima de su l�pida este valor de p (figura 122).
Aqu� esta:

3,14159265358979323846264338327950288
�Un tal Shenx en el a�o 1873 obtuvo un valor para p , donde despu�s de coma iban 707 decimales! Estos largos n�meros, expresando el valor de p aproximadamente no tienen valor practico, ni tampoco te�rico. Solamente en nuestra �poca, durante el ocio, pudieron aparecer las ganas de batir r�cords, superando a Shenx: En los a�os 1946 � 1947, Ferguson (universidad de Manchester) y Wrench (Washington) calculaban 808 decimales para p y estaban muy contentos porque encontraron errores en los c�lculos de Shenx, que comenzaban a partir del decimal n�mero 528.

Figura 122. Grabaci�n matem�tica encima la l�pida.

Por ejemplo, si dese�bamos encontrar longitud de ecuador terrestre con la exactitud de un cent�metro, sabiendo su di�metro, ser�a suficiente usar 9 decimales de p . Cogiendo el doble (18), hab�amos podido calcular longitud de la circunferencia, con el radio desde la Tierra hasta el Sol, equivoc�ndonos en no m�s de 0,0001 mm (�en 100 veces menores del pelo!).
Muy claramente ense�� la utilidad absoluta del primer centenar de decimales del numero p , el matem�tico ruso Grave. Hab�a calculando, si imaginamos una esfera, donde el radio es equivalente ala distancia desde la Tierra hasta Sirio, es decir, la cantidad de los kil�metros es equivalente a 132 con diez ceros: 132 � 10 ¹⁰ , llenando a esta esfera con microbios, donde en cada mil�metro cubico de esfera hay por mil millones 10 ¹⁰ de microbios, luego todos estos microbios se colocan sobre una l�nea recta as�, donde distancia entre cada un microbio era otra vez equivalente a la distancia desde Sirio hasta la Tierra, entonces, teniendo en cuenta este segmento fant�stico como di�metro de la circunferencia, era posible calcular longitud de la circunferencia gigantesca as� obtenida con una exactitud de 1/1.000.000 mm, utilizando 100 decimales despu�s de coma. Bien anota sobre este asunto un astr�nomo franc�s Arago, "en el sentido pr�ctico, nosotros no habr�amos ganado nada, si entre longitud de circunferencia y su di�metro hubiera existido la proporci�n exacta".
Para c�lculos habituales con el n�mero p es necesario recordar dos decimales despu�s de la coma (3,14), para los m�s exactos, los cuatros decimales (3,1416: en vez de 5 utilizaremos 6, porque luego sigue un decimal superior al 5).
Peque�os poemas o frases divertidas se quedaran en memoria m�s tiempo, que n�meros. Por eso para recordar mejor el significado num�rico de p inventan unos versos o frases especiales. En estas obras de poes�a matem�tica buscan palabras, donde la cantidad de letras de cada palabra coincide sucesivamente al numero correspondiente del p .
Hay versos en ingles de 13 palabras, por lo tanto dan 12 signos despu�s de coma; en alem�n, de 24 palabras, y en franc�s de 30 palabras.
Ellos son curiosos, pero muy grandes y pesados. Entre alumnos de E. Y. Tereskov , el profesor de matem�tica de una regi�n moscovita, hay una estrofa muy popular en la escuela inventada por el mismo:

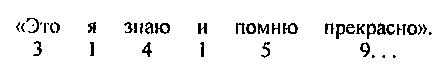
Una de sus alumnas, Elisa Cherikover invent� una siguiente frase ir�nica y practica:

El autor de este libro no atreve de inventar algo suyo, pero propone una frase bastante prosaica. "�Qu� yo lo se sobre c�rculos?", una pregunta, donde el n�mero 3,1416 esconde la respuesta.
Volver

3. El error de Jack London
El sitio siguiente de la novela de Jack London " Un due�o peque�o de una gran casa" deja para nosotros unos datos para los c�lculos geom�tricos:

Problema :
" En el medio del campo hay una p�rtiga de acero, puesta profundamente a la tierra, Desde la cima hasta el fin del campo viene el cable, fijado por el tractor. Mec�nicos aprietan la palanca, y el motor empieza a trabajar.
El veh�culo tira para adelante, circunscribiendo el c�rculo alrededor de la p�rtiga, como si fuera su centro.
- Para perfeccionar finalmente el veh�culo, - dijo Gregen, - os queda convertir la circunferencia, la que circunscribe el veh�culo, al cuadrado.
- Por cierto, en el campo cuadrado de este modo se elimina mucha tierra.
- Gregen hizo un par de c�lculos, luego dijo:
- Se pierde, aproximadamente tres acres de cada diez.
- No menos." Proponemos a los lectores comprobar el c�lculo.

Soluci�n
El c�lculo ha sido err�neo: Se pierde 0,3 de toda la tierra. Pues bien, en realidad, un lado del cuadrado es a. La superficie de este cuadrado es a ² . Di�metro del circulo inscrito es equivalente a, su superficie


La parte limitada de la plaza cuadrada es:


Vemos que la parte bruta del campo cuadrado esta formado no 30%, como pensaban protagonistas de novela americana, sino 22%.
Volver

4. Lanzamiento de aguja
Un modo original e espont�neo para c�lculo de p es el siguiente. Aprovisionando con una aguja corta (de dos cent�metros), mejor sin punta, para que aguja sea del mismo espesor, se dibujan en un papel un par de l�neas paralelas, separadas una de otra por el doble de la longitud de la aguja. Luego se arroja la aguja de una altura arbitraria sobre el papel y se marca, ha cruzado o no la aguja una de las l�neas (figura 123 de la izquierda). Para que la aguja no rebote, se deja por debajo, un papel secante o un pa�o. Se repite el lanzamiento muchas veces, por ejemplo cien o mejor, mil de veces, marcando cada vez el sitio de intersecci�n. Luego se divide la cantidad total de lanzamientos sobre el n�mero de acontecimientos, cuando la aguja ha ca�do sobre las rayas, entonces, el resultado ser� �l numero p , por supuesto, mas o menos aproximadamente.

Figura 123. Lanzamiento de aguja. Experimento de Buf�n

Explicaremos por qu� el resultado es as�. Llamaremos K a la probabilidad de intersecci�n y la longitud de la aguja ser� 20 mm.
Entonces la cantidad probable de intersecciones de cada mil�metro de aguja es K/20 . Para una parte la aguja de 3 mm, ser� 3K/20 y para una porci�n de 11 mm ser� 11K/20 y etc. Entonces la cantidad probable de intersecciones es directamente proporcional a la longitud de aguja.
Esta proporcionalidad se mantiene a�n en el caso que la aguja sea curva. Ser� mejor si la aguja tiene la forma de la figura II (figura 123 a la derecha), adem�s la parte AB = 11 mm y BC = 9 mm.
Para parte AB la cantidad de intersecciones probables es 11K/20 y para BC es 9K/20 y para la aguja completa ser� 11K/20 + 9K/20, es decir, como antes es equivalente a K. Podemos doblar la aguja de una manera todav�a m�s ingeniosa (la figura III, figura 123), la cantidad de intersecciones no cambiar�.
(Tengan en cuenta, que con una aguja doblada son posibles intersecciones con dos o m�s partes de la aguja en el mismo momento; Esa intersecci�n la tenemos que calcular como 2, como 3 y etc., porque la primera ha sido tomada c�lculos de intersecciones para una parte de aguja, la segunda, para otra y etc.)
Imaginase ahora, que estamos lanzando una aguja en forma del c�rculo, con di�metro equivalente a la distancia entre las l�neas (es el doble mas de nuestra aguja). Este anillo debe cada vez cruzar alguna l�nea (o tangente a ambas l�neas, en todo caso, veremos dos intersecciones). Si la cantidad total de lanzamientos es N, entonces �l numero de encuentros es 2N. Nuestra aguja recta es menor de este anillo en tantas veces, en cuantas veces el medio di�metro es menor de la longitud de circunferencia, es decir, en 2 p veces. Pero nosotros ya tenemos establecido, que la cantidad probable de intersecciones es proporcional a la longitud de aguja. Por eso el n�mero probable (K) de las intersecciones por nuestra aguja tiene que ser menos de 2N en 2 p veces, es decir, equivalente a




Cuando mayor sea la cantidad de lanzamientos, m�s exacto ser� el valor para p . Un astr�nomo suizo R. Volf en siglo XIX observ� 5000 ca�das de aguja sobre el papel rayado y ha obtenido la cantidad de p = 3,159� esta expresi�n es menos exacta que el n�mero del Arqu�medes.
Como vemos, la proporci�n de longitud de la circunferencia sobre el di�metro aqu� buscan siguiendo por el camino practico, adem�s, es curioso, no hace falta dibujar el c�rculo o di�metro, es decir, no falta el comp�s. Una persona sin tener ni idea sobre geometr�a o sobre el c�rculo, podr� encontrar la cantidad del numero p , si pacientemente hace bastante mayor cantidad de lanzamientos con aguja.
Volver

5. Enderezamiento de circunferencia
Para mayor�a de los prop�sitos pr�cticos es bastante utilizar para el p un numero 3 1/7 y el largo de la circunferencia equivalente a 3 1/7 veces el di�metro (dividiendo un segmento sobre siete partes es, evidentemente, f�cil). Existen otros modos aproximadamente de enderezamiento, utilizados en la practica por carpinteros y etc. No vamos a examinar ahora ellos, sino mostraremos un modo de enderezamiento bastante f�cil, el que deja un resultado muy exacto.

Problema
Si necesitamos enderezar la circunferencia O del radio r (figura 124), entonces pasaran el di�metro AB, y en el punto B � una l�nea perpendicular CD hacia AB. Desde el centro O sobre �ngulo de 30� hacia AB pasan la recta OC. Luego en la recta CD desde el punto C dejan los tres radios de esta circunferencia y unen el punto D recibido con A: El segmento AD es equivalente a longitud de la media circunferencia. Si el segmento AD prolongaremos doble, entonces recibiremos la circunferencia O enderezada. El error posible menos de 0,0002r.

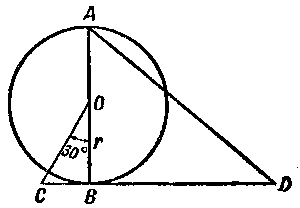
Figura 124. El modo aproximadamente geom�trico de enderezamiento de la circunferencia. �Cu�l es el principio elemental de esta teor�a?

Soluci�n
Por el teorema de Pit�goras

CB ² + OB ² = OC ² .
Indicando el radio OB otra vez de r y teniendo en cuenta, que CB = OC/2 (como el cateto que est� frente del �ngulo de 30�), obtenemos:


De donde


Luego en el tri�ngulo ABD

Comparando este resultado con aquel que obtuvimos, si cogemos p con la mayor potencia de exactitud ( p = 3,141593), vimos, que la diferencia forma solamente 0,00006 m. Si nosotros de esta manera enderezaremos la circunferencia con el radio de 1 m, el error ser� para media circunferencia solamente 0,00006 m, y para circunferencia total 0,00012 m, o 0,12 mm ( es la triple anchura del pelo).
Volver

6. Cuadratura del c�rculo
No puede ser, que ninguno de Uds. no escucharan alguna vez sobre la "cuadratura del c�rculo", sobre aquella famosa tarea de geometr�a, con la cual trabajaban matem�ticos veinte siglos antes. Estoy seguro, que hay lectores que ellos mismos probaron solucionar esta tarea. Y aun m�s, lectores que est�n perplejos de la dificultad de esta tarea cl�sica e insoluble. La mayor�a acostumbrados de repetir lo mismo, que la tarea sobre la cuadratura del c�rculo es irresoluble, no sabiendo nada de la naturaleza de este problema, ni nada sobre dificultad de la soluci�n.
La Matem�tica tiene muchas tareas todav�a m�s curiosas como te�rica y pr�cticamente de la cuadratura del circulo. Pero ninguna ha tenido tanto popularidad como esta; durante siglos han trabajado sobre ella profesionales, matem�ticos y aficionados.
"Encontrar la cuadratura del circulo", es entonces, dibujar un cuadrado cuya superficie sea equivalente a la de un c�rculo dado. Pr�cticamente esta tarea aparece a menudo, pero tal vez se soluciona pr�cticamente. La tarea famosa pide, para que el figura sea totalmente correcta, construirlo con la ayuda de dos tipos de operaciones t�cnico � lineales:
1.Circunscribir la circunferencia alrededor de un punto
2.Pasar la l�nea recta a trav�s de dos puntos.
O sea, necesita hacer la figura, utilizando solamente dos instrumentos: comp�s y regla.
Entre los matem�ticos hay mayor extensi�n de opini�n, que la dificultad condicionada por aquello, que la proporci�n de la longitud de la circunferencia sobre el di�metro (el famoso numero p ) no puede ser expresado por una cantidad determinada de d�gitos. Es cierto en tanto que soluci�n de esta tarea depende de la naturaleza especial del numero p . En realidad: Transformaci�n del rect�ngulo al cuadrado con la misma superficie es una tarea f�cil y r�pida de solucionar. Para el problema de cuadratura del circulo tiene su expresi�n en la construcci�n, por el comp�s y regla, de un rect�ngulo isom�trico al c�rculo. De la f�rmula de la superficie de una circunferencia S = p r ² , o (que es lo mismo) S= p r � p r, evidentemente, superficie del circulo es equivalente a la superficie de este rect�ngulo, donde uno de los lados es r, otro en p veces m�s. Entonces se trata de dibujar un segmento, el que en p veces ser� mas largo del dado. Se sabe, p no es exactamente equivalente a 3 1/7, ni 3,14, ni tampoco 3, 14159. La serie de los n�meros se lleva hasta el infinito.
Esta caracter�stica del numero p , su irracionalidad fue examinada en el siglo XVIII por los matem�ticos Lamber y Lejandro. Sin embargo, conocimientos de irracionalidad de p no hab�an parado a los esfuerzos de los" cuadroturistas" de matem�tica. Ellos sab�an, que la irracionalidad por si misma no hac�a la tarea desesperada. Existen cantidades irracionales, las que geometr�a sabe "construir" perfectamente. Si necesito dibujar un segmento, que sea m�s largo del dado en veces. El n�mero , como p , son irracionales. Sin embargo, no es nada tan f�cil, que dibujar el segmento buscado: Recordaremos, es el lado del cuadrado inscrito en el circulo con el radio a. Cualquier alumno har� la construcci�n del segmento (lado del tri�ngulo inscrito equil�tero). No hay grandes dificultades con la construcci�n de una expresi�n irracional (de primera vista tan complicada)


porque la tiene su expresi�n en la construcci�n de 64- rinconera.
Como vemos, el multiplicador irracional, estado en la expresi�n, no siempre lo hace esta expresi�n imposible para construir con el comp�s y la regla. La insolubilidad de cuadratura del circulo se esconda no totalmente en p irracional, sino dentro de otra caracter�stica de este n�mero. Precisamente, la cantidad p no es algebraica, es decir no podemos obtenerlo como soluci�n de una ecuaci�n con coeficiente racional. Estos n�meros llaman "trascendental"
El matem�tico de siglo XVI el Viet demostr�, que el numero


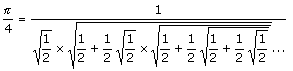
Esta expresi�n para p soluciona la tarea de la cuadratura del c�rculo, si la cantidad de las operaciones entre su serie finita (despu�s esta expresi�n podr� ser construida geom�tricamente). Pero como cantidad de expresiones de ra�ces cuadradas en este caso es infinita, entonces la f�rmula de Vieta no ayuda.
Pues el motivo de la insolubilidad de la tarea sobre cuadratura del circulo es el transcendentalismo del n�mero p , es decir no se podr� solucionar la ecuaci�n con coeficientes racionales. Esta caracter�stica del numero p ha sido examinada por el matem�tico alem�n Lindeman en a�o 1889. En el fondo este cient�fico es la �nica persona que ha solucionado la cuadratura del circulo, a pesar que la soluci�n es, afirma, de construcci�n imposible. Por lo tanto, en a�o 1889 se terminan esfuerzos seculares de los matem�ticos en este sentido; pero, por desgracia, no terminan los ensayos in�tiles de los aficionados, que conocen insuficientemente el problema.
Lo anterior se deduce de la teor�a, pero, �qu� pasa con la pr�ctica? Pues ella no necesita una resoluci�n justa de esta tarea famosa. La opini�n de mayor�a, es una resoluci�n sobre el problema de cuadratura del circulo, quiz�s tendr�a gran significaci�n para la vida practica si se tiene una equivocaci�n profunda. Para las necesidades habituales es suficiente tener a disposici�n los modos aproximados de soluci�n.
Las averiguaciones pr�cticas de la cuadratura del c�rculo han sido in�tiles desde aquel tiempo, cuando se ten�an los primeros 7 u 8 n�meros exactos de p . Para necesidades de vida practica es suficiente saber, que p = 3,1415926. Ninguna medici�n de longitud puede dar un resultado expresado por mas de siete cifras significativas. Por eso, tomar para p mas de ocho cifras decimales, es in�til: la exactitud del c�lculo no se mejorar�.
Si el radio est� expresado por siete n�meros significativos, entonces la longitud de la circunferencia no tendr� mas de siete n�meros, aunque cojamos para las primeras cien cifras significativas.
En aquello, que los matem�ticos antiguos lo hicieron con gran trabajo para obtener las cifras significativas m�s largas, no tiene ninguna importancia pr�ctica. Adem�s la significaci�n cient�fica de esta obra es in�til. Sencillamente se trata de paciencia. Si Uds. tienen ganas y mucho tiempo ocioso, podr�n encontrar 1000 signos para p , utilizando la serie siguiente infinita, encontrada por el Leibinz


Un astr�nomo, citado anteriormente, Argo, tiene escrito lo siguiente:
"Buscadores de cuadratura del circulo siguen dedicando el tiempo al solucionar la tarea, imposibilidad de la cual ahora esta examinada positivo y la cual, si por acaso pudiera realizarse, no traer�a ning�n inter�s practico. No hace falta ocup�ndonos sobre este asunto: Los enfermos de cerebro hagan todo lo posible para descubrir la cuadratura del circulo, pero por desgracia no tiene ning�n sentido. Esta enfermedad mental existe de la antig�edad."
Y termina ir�nicamente:
"Las academias de todos pa�ses, enfrent�ndose contra los buscadores de cuadratura, anotaban un fen�meno, que la enfermedad, habitualmente, progresa en la primavera."
Volver

7. Tri�ngulo de Bingo
Examinaremos una de las soluciones aproximadas del problema sobre cuadratura del circulo, muy c�moda para las necesidades practicas de la vida.
El modo consiste en que se calcula (figura 125) el �ngulo a, bajo de cual deberemos pasar hacia di�metro AB a la cuerda AC = x, era el lado del cuadrado buscado. Para saber el valor de este �ngulo, tenemos que pedir ayuda a la trigonometr�a:


donde r es el radio del circulo.

Figura 125. Un modo de ingeniero ruso de Bingo (1836)

Entonces, un lado del cuadrado buscado x = 2r � cos a, su superficie es 4r ² � cos ² a. Por otro lado, la superficie del cuadrado p r ² es la superficie del circulo correspondiente. De aqu� se deduce,

4r ² � cos ² a = p r ²
de donde

cos ² a =

cos a = = 0,886.
En las tablas encontramos:
a = 27� 36'.
Entonces, pasando en el mismo circulo la cuerda bajo de 27� 36' sobre el di�metro, inmediatamente obtenemos un lado del cuadrado, la superficie del cual es equivalente a la superficie del circulo. Pr�cticamente se hacen as�: preparan el tri�ngulo t�cnico, donde uno de los �ngulos agudos es de 27� 36' (el otro 62� 24' ). Teniendo a su disposici�n este tri�ngulo, podemos, para cada un circulo, encontrar un lado del cuadrado isom�trico.
Para personas quienes deseen preparar este tri�ngulo t�cnico son �tiles las indicaciones siguientes.
Como la tangente de 27� 36' es equivalente a 0,523, o 23/44, entonces los catetos de este tri�ngulo est�n en la proporci�n de 23/44. Por eso, preparando el tri�ngulo, uno de los catetos, por ejemplo, es de 22 cm, y el otro 11,5 cm, nosotros vamos a tener todo lo que necesitamos. Esta claro, que podemos utilizar este tri�ngulo como otro cualquiera.
Volver

8. La cabeza y los pies
Parece, que uno de los protagonistas de Julio Verne calculaba, cu�l parte de su cuerpo hab�a pasado un camino mas largo durante el tiempo de los cruceros alrededor del mundo, la cabeza o los pies. Esta tarea es m�s instructiva, si preguntamos de otra manera. Nosotros la proponemos en otro aspecto.

Problema .
Imag�nense que Uds. han cruzado el mundo a lo largo de ecuador. �En cu�nto la cima de la cabeza pasara el camino mas largo, que la punta del pie?

Soluci�n
Los pies recorrieron un camino 2 p R, donde R es el radio del globo terrestre. La cima de cabeza andaba sobre esto 2 p (R + 1,7), donde 1,7m es la estatura del cuerpo humano. La diferencia de los caminos es 2 p ( R + 1,7) - 2 p R = 2 p � 1,7 = 10,7m. Entonces, la cabeza hab�a recorrido un camino en 10,7 m mayor, que los pies.
Es curioso, que en la respuesta final no entra el radio de la Tierra. Por eso el resultado sale lo mismo en la Tierra, como en J�piter, u otro planeta peque�o. En general, la diferencia de longitudes de dos circunferencias conc�ntricas no depende de sus radios, solamente de las distancia entre ellos. Adici�n de un cent�metro del radio de la �rbita terrestre aumentar� su longitud en tantas veces, en cuantas prolonga esa adici�n al radio de una simple moneda.
M�s sobre esta paradoja geom�trica se encuentra en uno de los manuales de distracciones geom�tricas.

Problema .
�Si se pone sobre el ecuador terrestre un hilo met�lico y luego se le a�ade un metro, entonces, podr� pasar un rat�n entre alambre y tierra?

Soluci�n.
Normalmente contestan, que el espacio era mas estrecho que un pelo: �Qu� significa un metro comparando con 40 millones de metros de ecuador terrestre! En realidad el espacio es


No solo un rat�n, sino tambi�n el gato podr� pasar por este espacio.
Volver

9. Alambre a lo largo de ecuador

Problema.
Ahora imag�nense, que el globo terrestre esta cubierto fuertemente por un hilo met�lico a lo largo de ecuador. �Qu� suceder�, si el hilo se enfr�a en 1� C? �Considerando que no se rompe o no se estira, entonces, cuanto se hunde dentro de la tierra?

Soluci�n.
Parece, que no es tan importante la bajada de temperatura solamente de 1�C, no podr� provocar hundimiento profundo del alambre en la tierra. Los c�lculos dicen lo siguiente.
Enfri�ndose en 1� C, el hilo met�lico reduce un cien mil parte de toda su longitud. Con longitud de 40 millones de metros (es la longitud de ecuador) el hilo tiene que reducirse, como es f�cil de calcular, sobre 400m. Pero el radio de esta circunferencia met�lica se reduzca no en 400 metros, sino mucho mas menos. Para saber, en cuantas veces disminuye el radio, debemos dividir 400 m sobre 6,28, es decir sobre 2 p . Obtendremos como 64 metros. Entonces el hilo enfri�ndose en 1� C, tendr�a sobre estas circunstancias que hundirse en la tierra no en par de cent�metros, �sino m�s que en 60 metros!
Volver

10. Acci�n y c�lculo

Problema:
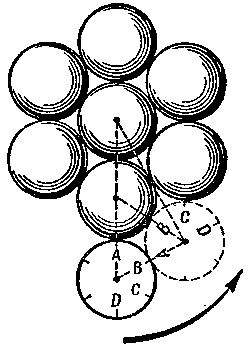
Enfrente de Uds. hay ocho c�rculos iguales (figura 126). Los siete pintados � son inm�viles, octavo (claro) corre encima de ellos sin deslizarse. �Cu�ntas vueltas darie el, dando una vuelta alrededor de los c�rculos inm�viles?

Figura 126. �Cu�ntas vueltas har� el circulo claro, dando un giro alrededor de otros siete?

Uds. ahora mismo podr�n comprobar en la practica: Poniendo encima de la mesa ocho monedas del mismo tama�o, colocando como se indica el figura y fijando las siete monedas sobre la mesa, dejando moneda octava hacer una vuelta. Para saber la cantidad de vueltas f�jense, por ejemplo, a la postura del numero encima de moneda. Cuando el numero se vuelva a ponerse en la postura principal, la moneda habr� dado un giro alrededor de su centro.
Hagan la prueba en realidad, no imagin�ndola, y ver�n, que la moneda har� solo cuatro vueltas.
Ahora vamos a probar de obtener la misma respuesta con ayuda de reflexi�n y c�lculos. Vamos a encontrar, por ejemplo, el que arco circunscribe el circulo corriente encima del circulo inm�vil. Con esta raz�n imaginaremos movimiento del circulo corriente desde la "colina" A en la "valleja"(quebrada) pr�xima entre dos c�rculos inm�viles (figura 126 la raya discontinua).
Sobre la figura no es tan dif�cil de establecer, que el arco AB, sobre el que corr�a el circulo, sea de 60� . En la circunferencia de cada circulo inm�vil aquellos arcos son dos; Juntos ellos forman el arco de 120� � 1/3 de circunferencia.
Por lo tanto, el circulo corriendo haga 1/3 de vuelta, dejando 1/3 de cada uno circulo inm�vil.
Todos juntos los seis c�rculos inm�viles; Pues la respuesta es: el c�rculo m�vil hace solamente 1/3 � 6 = 2 vueltas.
�Pues estamos con los diferentes resultados de observaci�n! Pero "la acci�n es cosa caprichosa". Si la observaci�n no confirma el calculo, entonces hay dentro del c�lculo un defecto.
Uds. tendr�n que encontrar el defecto en los siguientes razonamientos.

Soluci�n.
Es que pasa, cuando el circulo corre sin deslizamiento sobre el segmento recto con � de longitud de la circunferencia del circulo corriente, entonces en realidad hace � vuelta alrededor de su centro. Esta aprobaci�n parece injusta, no corresponda a realidad, cuando el circulo corre sobre el arco de alguna l�nea curva. En la tarea examinada el circulo corriente, recorriendo el arco, formado, por ejemplo, 1/3 longitud de su circunferencia, hace no 1/2 vuelta, sino 2/3 vueltas y por lo tanto, recorriendo a los seis arcos har�n
6 � 2/3 = 4 vueltas!
Podemos asegurarnos observ�ndola. La raya punteada en el figura 126 refleja esa posici�n
del circulo corriente despu�s de que �l recorri� sobre el arco AB ( =60� ) del circulo inm�vil, es decir, sobre el arco formado por 1/6 longitud de la circunferencia. En la nueva posici�n del circulo el sitio mas alto sobre su circunferencia ocupa ahora no el punto A, sino el punto C, como vemos corresponda al giro de los puntos de circunferencia sobre 120� , es decir, sobre � de vuelta completa. Al "camino" de 120� corresponda 2/3 de vuelta completa del circulo corriente.
Entonces, si el circulo corre sobre una l�nea curva, el har� otra cantidad de vueltas, que cuando el corre sobre un camino recto de la misma longitud.

* * *
Nos detendremos un poco sobre la parte geom�trica de este fen�meno curioso, adem�s, la explicaci�n habitual no siempre es segura.
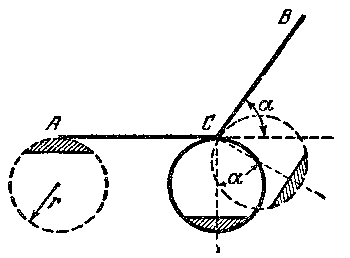
Sea el circulo con radio r que corre sobre la recta. El hace una vuelta sobre el segmento AB, longitud de cual es equivalente a la longitud de circunferencia del circulo corriente (2 p r). Doblaremos el segmento AB por la mitad (figura 127) y daremos la vuelta con CB sobre �ngulo a proporcionalmente a la postura principal.

Figura 127. Como aparece la vuelta suplementaria con la ida del circulo sobre la l�nea curva.

Ahora, cuando el circulo esta haciendo media vuelta, alcanza a la cima C y, para mantener esta postura, sobre cual el iba a tocar en el punto C a la recta CB, girar junto con su centro sobre el �ngulo, equivalente a a (estos �ngulos son iguales, porque tienen mutuamente los lados perpendiculares).
Durante el giro el circulo corre sobre el segmento. Esto es que produce aqu� la parte suplementaria de la vuelta completa comparando con el giro sobre la recta.
La curva suplementaria forma aquella parte de la vuelta completa, cual esta formando el �ngulo a desde el �ngulo 2 p , es decir, media vuelta, entonces, en total con el movimiento sobre la l�nea quebrada ACB �l har� 1 + a /2 p vueltas.
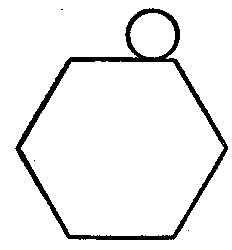
Ahora no es dif�cil de imaginar, cuantas vueltas tiene que hacer el circulo, corriendo por la parte exterior del hex�gono (figura 128).

Figura 128. �En cuantas vueltas mas har� el circulo, si el correr� encima de los lados del pol�gono, pero no sobre su per�metro enderezado?

Evidentemente tanto, cuantas veces �l dar� vueltas sobre el camino recto, equivalente al per�metro (suma de los lados) del hex�gono, plus la cantidad de vueltas, equivalente a la suma de los �ngulos exteriores del hex�gono, dividida por 2 p . Como la suma de los �ngulos exteriores de cualquier pol�gono convexo es justa e equivalente a 4d, o 2 p , entonces 2 p /2 p = 1.
De este modo, rodeando al hex�gono y tambi�n cualquier pol�gono convexo, el circulo siempre har� con una vuelta mas, que con movimiento sobre el segmento recto, equivalente al per�metro del pol�gono.
Duplicaci�n infinita a los lados del pol�gono convexo y justo esta acerc�ndose a la circunferencia, significa, todas las consideraciones dichos tienen la misma importancia para circunferencia. S�, por ejemplo, de acuerdo con el problema principal un circulo corre sobre el arco de 120� equivalente a su circulo, entonces, la confirmaci�n, que el circulo movido hace no 1/3, sino 2/3 de vueltas, tendr� la claridad geom�trica completa.
Volver

11. Chica encima de una cuerda
Cuando circulo corre encima de una l�nea, estado con el en mismo plano, entonces el cada punto del circulo se mueve sobre el plano, es decir, tiene su trayecto.

Figura 129. Cicloide � el trayecto del punto A del disco, corriendo sin deslizamiento sobre la rectil�nea.

F�jense en la trayectoria de cualquier punto del circulo, corriendo encima de una l�nea o encima de una circunferencia, y Uds. podr�n ver curvas distintas.
Algunas de ellas estas reflejadas en los figuras 129 e 130.
Surge una pregunta: �Podr� un punto del circulo, corriendo por la "parte inferior" de la circunferencia de otro circulo(figura 130), inscribiendo no l�nea curva, sino la recta? En primer lugar parece imposible.
Sin embargo esta construcci�n la vi por mis propios ojos. Ha sido un juguete "la chica en la cuerda"(figura 131). Uds. podr�n prepararlo tambi�n sin ninguna dificultad. En un trozo de cart�n dibujan un circulo con di�metro de 30 cm, dejando el campo en el papel, y uno de los di�metros prolongan por ambas partes.

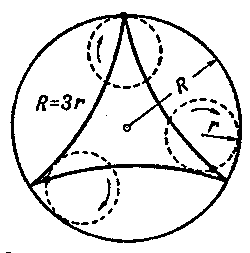Figura 130. Hipocicloide, el trayecto del punto de la circunferencia del disco, corriendo por el dentro de gran circunferencia, adem�s R = 3r.

Sobre el di�metro prolongado por ambas partes colocaremos agujas con hilo, estirando al horizontalmente y ambas sus fines fijar encima del cart�n. El circulo dibujado se cortara y dentro de ventanilla creada ponen un circulo tambi�n de cart�n con di�metro de 15cm.
Sobre el borde del circulo peque�o colocan una aguja, como en el figura 131, cortan del papel la figura de la chica y se pegan por la pierna sobre cabeza de aguja.
Ahora prueban a rodar el circulo menor, ajust�ndose al borde de la ventanilla; La cabeza de aguja, junto con ella figura de chica van a deslizarse hacia delante, y detr�s a lo largo del hilo tirante.

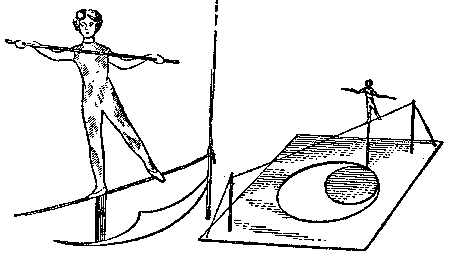Figura 131. "La chica en la cuerda". En el circulo corriente hay unos puntos, los cuales se mueven rectamente.

Esto se explica solo, porque el punto del circulo corriente, donde esta fijada la aguja, se mueve justamente a lo largo del di�metro de ventanilla
�Pero por qu� en el caso an�logo, reflejando en la figura 130, el punto del c�rculo corriente inscribe no la recta, sino la l�nea curva (se llama hipocicloide)? Todo depende de la proporci�n sobre los di�metros de ambos c�rculos.

Problema
Demostrar, que si dentro de un circulo mayor corre un circulo doble menor de su di�metro, entonces durante este movimiento cualquier punto sobre circunferencia del circulo menor se mover� sobre rectil�nea, la cual es el di�metro del circulo mayor.

Soluci�n.
Si el di�metro del circulo O ₁ el doble menor del di�metro del circulo O (figura 132), entonces en cualquier momento de movimiento del circulo O ₁ , uno de su punto esta en el centro del circulo O.

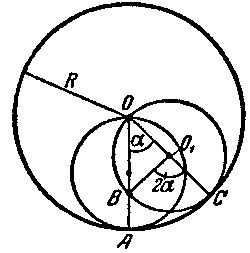Figura 132. Explicaci�n geom�trica " la chica en la cuerda"

Observaremos el movimiento del punto A. Sea el circulo menor que se ha recorrido sobre arco AC.
�D�nde se encontrar� el punto A en el nuevo estado del circulo O ₁ ?
Evidentemente que debe encontrarse en tal punto B de su circunferencia, para que los arcos AB y BC sean iguales de longitud (circulo se corre sin deslizarse).
Sea OA = R y � AOC = a .
Luego AC = R a ; por lo tanto, BC = R a , pero como O ₁ C = R/2 , entonces

� BO ₁ C = R � a /(R/2) = 2 a
Luego � BOC como inscrito es 2 a / 2 = a , es decir, el punto B se ha quedado en la recta OA.
El juguete descrito aqu� representa por si mismo un mecanismo primitivo para transformaci�n del movimiento giratorio rectil�neo.
La construcci�n de estos mecanismos (se llaman inversores) interesa a los t�cnicos � mec�nicos desde el tiempo de primer inventor ruso de la maquina de vapor � I. I. Polzunov. Normalmente estos mecanismos, transmiten al punto el movimiento rectil�neo, tienen estructura de charnelas.
Una valiosa aportaci�n en la matem�tica de los mecanismos hizo el matem�tico ruso P.L. Chebyshev (1821 � 1894) (figura 133). El era no solo un matem�tico generoso, sino tambi�n gran mec�nico. Construy� un modelo de la silla "cicleta", invent� el mejor mecanismo contable de aquel tiempo � aritm�metro y etc.

Figura 133 P. L. Chebyshev (1821 - 1894)

Volver

12. Un vuelo a trav�s del Polo
Uds. evidentemente, se acuerdan de un vuelo del famoso M M. Gromov y sus compa�eros desde Mosc� a San Jacinto a trav�s del Polo norte, cuando durante 62 horas 17 min. de vuelo han sido conquistados dos marcas mundiales de un vuelo sin aterrizaje sobre una l�nea recta (10.200 km) y sobre la curva (11.500 km).
�C�mo piensan Uds, ser� posible que el avi�n de los h�roes dio la vuelta alrededor del eje terrestre junto con la Tierra, y adem�s cruzando el Polo? Esta pregunta se escucha a menudo, pero no siempre nos dan la respuesta correcta. Cualquier avi�n, tambi�n aquel, que cruz� el Polo, sin duda alguna tendr� que tomar parte de la vuelta del globo terrestre. Esto aparece, por que el avi�n volando esta solamente separado con la litosfera, pero se queda en atm�sfera y lleva tras si en el movimiento alrededor del eje de nuestro planeta.
Entonces, haciendo el vuelo desde Mosc� hasta Norteam�rica, el avi�n en el mismo tiempo giraba junto con la Tierra alrededor de su eje. �Cu�l es el trayecto de este vuelo?
Para contestar correctamente, debemos que tener en cuenta que cuando digamos "el cuerpo se mueve", es decir, se cambia de postura del cuerpo con respecto de otros. La pregunta sobre el camino y en general sobre el movimiento no tendr�a sentido, si no est� indicado, como dicen matem�ticos, el sistema de referencia, o sencillamente, un cuerpo, respecto al cual aparece el movimiento.
Relativo a la Tierra el avi�n de M M. Gromov se ha movido casi a lo largo de meridiano Mosc�, como cualquier otro, gir� junto con la Tierra alrededor de su eje, manteniendo la l�nea de meridiano durante todo el vuelo; pero sobre la forma del camino para un observador de la Tierra este movimiento no se refleja, porque en este momento se aparece en relaci�n con otro cualquier cuerpo, no sobre la Tierra.
Por lo tanto, para nosotros, estando en la Tierra, el camino de este vuelo a trav�s del Polo, es el arco de un gran c�rculo, si tener en cuenta, que el avi�n se ha movido justamente sobre el meridiano y siempre sobre el mismo trayecto desde el centro de la Tierra.
Ahora preguntaremos de otra manera: tenemos el movimiento del avi�n con respecto a la Tierra y sabemos, que el avi�n con la Tierra junto giran alrededor de eje terrestre, es decir, tenemos el movimiento de avi�n y de la Tierra con respecto de un tal tercer cuerpo; �Cu�l es el camino de vuelo para el observador, en relaci�n con este tercer cuerpo?
Vamos a facilitar la tarea. La regi�n polar de nuestro planeta la imaginaremos como un disco plano, cuya superficie se sit�a perpendicularmente al eje terrestre. Sea esta superficie imaginaria aquel "cuerpo" respecto al cual se mueve el disco alrededor del eje terrestre, y a lo largo de un di�metro del disco regularmente corre una carreta mec�nica: La imagen del avi�n, volando a lo largo de meridiano a trav�s del Polo. �Qu� l�nea del camino va a presentar nuestra carreta en la superficie (mejor dicho, por un punto de la carreta, de su centro de gravedad)?
El tiempo, durante cual ella recorre desde un extremo del di�metro hasta otro, depender� de su velocidad.
Vamos a ver tres casos:

1. La carreta recorre su camino durante 12 horas;
2. El mismo camino recorre durante 24 horas y
3. Recorre durante 48 horas.

En cualquier caso el disco haga una vuelta durante 24 horas.

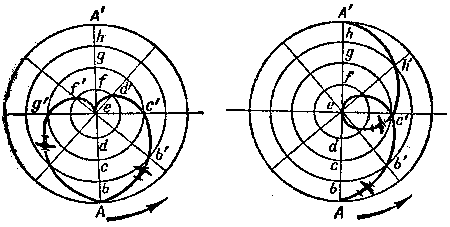
Figuras 134 y 135 Las curvas, las cuales inscribe un punto sobre una superficie inm�vil, participando durante dos movimientos.

Primer caso (figura 134). La carreta recorre el di�metro del disco durante 12 horas. El disco har� durante este tiempo media vuelta, es decir dar� vuelta de 180� , los puntos A y A' se intercambiaran a los sitios. En el figura 134 el di�metro esta dividido en ocho partes iguales, cada una de ellas, la carreta las recorre durante 12 / 8 = 1,5 hora.
Observaremos d�nde va estar la carreta despu�s de 1,5 hora de empezar la movida. Si el disco no da vueltas, la carreta, saliendo del punto A, alcanzo el punto b durante 1,5 hora. Pero el disco se gira y durante 1,5 hora seguir� sobre 180� / 8 = 45� . Por esto el punto b del disco se trasladar� al punto b' . Un observador, estado en el mismo disco y dando vuelta junto con �l no notar� su giro y ver�a, que la carreta cambia el sitio desde el punto A al punto b. Pero observador, el que se encuentra fuera del disco y no participa en su giro, notara otra cosa: La carreta se movi� sobre una l�nea curva desde el punto A al punto b' . A trav�s de otra 1,5 hora el observador, estado fuera del disco, se ve�a la carreta en el punto c' . A lo largo de otra 1,5 hora la carreta se mover� sobre el arco c' d' , luego de otra 1,5 hora alcanzara el centro e.
Siguiendo observando el movimiento de la carreta, el observador que est� afuera del disco, notar� algo inexpresable: la carreta inscribir� la curva ef' gf' A, y el movimiento, extra�amente, se terminar� no en el punto opuesto de di�metro, sino en el punto principal.
La clave de este enigma es siguiente: Durante seis horas de viaje sobre la otra mitad del di�metro el radio consigue dar vuelta junto con el disco sobre 180� y tomar la posici�n de primera mitad del di�metro. La carreta se gira con el disco tambi�n en aquel momento, cuando pasa por encima de su centro. Toda carreta no podr� entrar en el centro; ella se une con el centro solamente con un solo punto y en un momento dado �l se gira junto con el disco alrededor de este punto. Lo mismo tiene que pasar con un avi�n en este momento, cuando vuela por encima del Polo. Entonces el camino de la carreta sobre el di�metro del disco desde un punto final hasta otro para dos distintos observadores se presentaran las formas distintas del camino. Aquel, quien esta encima del disco y gira junto con �l, ese camino aparece como una l�nea recta. Pero para el observador inm�vil, no estado encima del disco, ver�a el movimiento de la carreta sobre una curva, reflejada en el figura 134 y recordara el contorno del coraz�n.
La misma curva la podr� ver cualquiera de Uds., observ�ndola desde el centro de la Tierra el vuelo de avi�n con respecto de superficie imaginario, perpendicularmente al eje terrestre, con una condici�n fant�stica, que la Tierra sea transparente, Ud. y la superficie no participan en el giro de la Tierra, y si el vuelo a trav�s del Polo duraba 12 horas.
Aqu� tiene un ejemplo curioso sumando las dos movidas.
En realidad el vuelo a trav�s del Polo desde Mosc� hasta el punto apuesto diametralmente del mismo paralelo duraba 12 horas, por eso quedaremos examinando otra tarea en el mismo sentido.
Segundo caso (figura 135). La carreta recorrer� el di�metro durante 24 horas. Durante este tiempo el disco cumple la vuelta completa, y por lo tanto para un observador inm�vil proporcionalmente al disco, el camino va a tener la forma de una curva, reflejada en el figura 135.

Figura 136. Una l�nea m�s curva saliendo en resultado al sumar dos movidas.

Figura 137. El camino Mosc� � San Jacinto como iba a presentarse para observador, sin Participando en vuelo, ni tampoco en giro de Tierra.

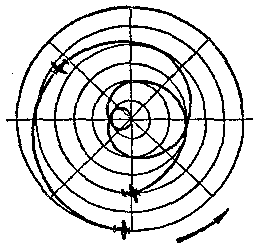
Tercer caso (figura 136) El disco como de antes cumple el giro completo durante 24 horas, pero la carreta viaja sobre el di�metro desde el fin hasta el fin durante 48 horas.
En este caso 1/8 de di�metro la carreta recorre durante 48 : 8 = 6 horas.
Durante aquellas seis horas el disco dar� la cuarta de su vuelta completa, de 90� . Por eso despu�s de seis horas desde el principio de movimiento la carreta se trasladar� sobre el di�metro (figura 136) en el punto b, pero el giro del disco trasladare ese punto en el punto b' . Despu�s de otras seis horas la carreta pasara en el punto g y etc. Durante 48 horas la carreta recorrer� todo el di�metro, y el disco hace dos vueltas completas. En vez de sumar estos dos movimientos para un observador inm�vil el camino le aparece como una curva recreativa, reflejada en el figura 136 por la l�nea continua.
Viendo este caso nosotros estamos acerc�ndose a los verdaderos condiciones del vuelo a trav�s del Polo. El vuelo dur� desde Mosc� hasta el Polo, aproximadamente, 24 horas; por ese observador, estando en el centro de la Tierra, se ver�a esta parte del camino como una l�nea, casi parecida a la primera mitad de la l�nea curva (figura 136). Que depende de otra parte del vuelo de M. M. Gromov, pues, ella duraba un y medio veces mas, adem�s, el trayecto desde el Polo hasta San Jacinto tambi�n es una y media veces mas larga, que la distancia desde Mosc� hasta el Polo Norte. Por eso el camino se representar� por la misma l�nea curva, �nicamente en un y medio veces mas larga.
La mayor�a de Uds., posiblemente, le confunda el obst�culo, donde el punto principal y final figura se refleja como los vecinos cercanos.
Pero no tenemos que perder de vista, que la figura le indica posici�n no simult�neamente de Mosc� y San Jacinto, sino separado por el lapso de 2 � del periodo de veinte cuatro horas.
Pues as� ha tenido la forma un camino por el Polo Norte, si podemos observar el vuelo, por ejemplo, desde el centro de la Tierra. �Pero si tenemos derecho de llamar este bucle dif�cil como un camino verdadero a trav�s del Polo en diferencia de relativo, reflejado en las cartas? No, ese movimiento tambi�n es relativo: El movimiento esta relacionando con un tal cuerpo, el que no participa en el giro de la Tierra alrededor de su eje, lo mismo que el figura del camino relativo a la superficie de la Tierra giratoria.
Si nosotros podemos observar el mismo vuelo desde la Luna o del Sol, el camino del vuelo tendr�a otro aspecto.
La Luna no comparte el giro terrestre de veinte cuatro horas, pero ella da la vuelta alrededor de nuestro planeta durante un mes. Durante 62 horas del vuelo desde Mosc� a San Jacinto, la Luna ha podido inscribir alrededor de Tierra un arco de 30� , y esto no podr�a no depender del trayecto del vuelo para un observador de la Luna. En el camino de avi�n, observado con respecto del Sol, aparec�a el tercer movimiento, el giro de Tierra alrededor del Sol.
"El movimiento del cuerpo aislado no existe, �nicamente existe movimiento relativo", - dijo F. Engels en la "Dial�ctica de la naturaleza".
La tarea examinada ahora aseg�ranos en esto.
Volver

13. Longitud de la correa de transmisi�n
Cuando los alumnos de escuela profesional terminaron su trabajo, el maestro al despedirse propuso solucionar un

Problema
"Para una de las nuevas instalaciones de nuestro taller, dijo el maestro, se necesita ensamblar la correa de transmisi�n, pero no sobre dos poleas, como era normalmente, sino sobre las tres, y el maestro les ense�� el esquema de la transmisi�n (figura 138).

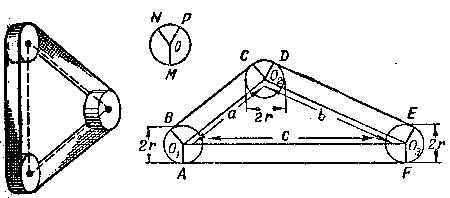
Figura 138. El esquema de transmisi�n. �C�mo encontrar la longitud de la correa de transmisi�n, utilizando solamente las medidas dadas?

Las tres poleas, continuaba �l, tienen las mismas medidas. Sus di�metros y las distancias entre sus ejes son indicadas en el esquema.
�C�mo, sabiendo estas medidas y sin hacer mediciones suplementarias, encontrar r�pido la longitud de la correa de transmisi�n?"
Los alumnos empezaron a pensar. De pronto alguno de ellos dijo:
" Penso, que toda dificultad es, que no est�n indicadas las medidas de los arcos AB, CD, EF, sobre cual la correa enarca cada uno de rodillos. Para encontrar la longitud de cada arco necesitamos saber el valor de �ngulo central y, a m� me parece, sin transportador no se arreglar�."
"Los �ngulos, de los que estas hablando, contestaba el maestro, podemos calcular sobre las medidas indicadas en el figura con ayuda de las f�rmulas y tablas trigonom�tricas, pero este camino es muy largo y dif�cil. Tambi�n no necesitaremos aqu� el transportador, por que no hace falta saber longitud de cada uno arco, es suficiente saber�".
"Su suma, dijeron los chicos, dando cuenta de qu� se trata" .
"Bueno, pero ahora os vais a casa y ma�ana trajerais vuestras soluciones."
No teng�is la prisa de conocer la soluci�n, la cual trajeron los chicos.
Despu�s de todo, con lo que ha dicho el maestro no es dif�cil solucionar por si mismo.

Soluci�n.
En realidad, la longitud de la correa se encuentra muy f�cil: A la suma de la distancia entre ejes de rodillos hay que a�adir la longitud de la circunferencia de una polea. Si la longitud de la correa es l, entonces

l = a + b + c + 2 p r
Sobre aquello, que la suma de las longitudes de arcos, con los cuales esta en contacto la correa, forma la longitud total de una polea, encontraron la clave todos los alumnos, pero demostrar una soluci�n ha sido dif�cil para algunos.
De las todas soluciones el maestro ha preferido la mas corta el siguiente.
Sea BC, DE, FA, son tangentes a las circunferencias (figura 138). Pasaremos los radios en los puntos del contacto. Como las circunferencias de las poleas tienen mismos radios, entonces las figuras O ₁ BCO ₂ , O ₂ DEO ₃ y O ₁ O ₃ FA, son rect�ngulos, por lo tanto,

BC + DE + FA = a + b + c.
Deja ense�ar, que la suma de las longitudes de arcos AB + CD + EF se forman la longitud completa de circunferencia.
Para esto construiremos la circunferencia O con el radio r (figura 138 arriba). Pasamos OM || O ₁ A, ON || O ₁ B y OP || O ₂ D, luego � MON = � AO ₁ N, � NOP = � CO ₂ D, � POM = � EO ₂ F, como los �ngulos con lados paralelos.

Figura 139. Necesito traducir del figura a las medidas necesarias y calcular la longitud de la cinta de transmisi�n.

De aqu� se deduce, que

AB + CD + EF = MN + NP + PM = 2 p r.
Entonces la longitud de la correa es

l = a + b + c + 2 p r.
Con el mismo modo podemos ense�ar, que no solamente para tres, sino para cualquier cantidad de las poleas iguales, la longitud de la correa de transmisi�n ser� equivalente a la suma de los intervalos entre sus ejes mas la longitud de la circunferencia de una polea.

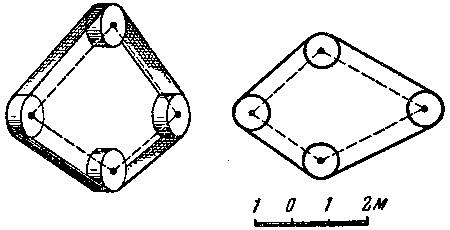
Problema .
En el figura 139 hay un esquema de la transmisi�n a cuatro ruedas (tambi�n hay ruedas intermedias, pero el esquema no incluye, como no tiene gran influencia para soluci�n). Utilizando la escala, indicada en el figura, introduzcan las medidas necesarias y calculen la longitud de la cinta .
Volver

14. Una tarea sobre la corneja prudente
Nuestros manuales escolares tienen una historia de "una corneja muy prudente". Esta historia antigua cuenta de una corneja, muerta de sed ha encontrado un jarro con agua. Hab�a muy poca agua en el jarro, y con el pico no ha sido posible conseguirla, pero la corneja cay� en la cuenta como ayudarse a s� misma. Comenz� a tirar los pedruscos en el jarro. En resultado de esta argucia hizo subir el nivel de agua hasta los bordes, y la corneja ha podido tomar el agua.
No vamos a entrar en este asunto, si puede haber una corneja tan inteligente. El caso nos interesa de parte geom�trica. Deja motivo para examinar la siguiente

Problema.
�Habr�a podido tomar la corneja si el agua hubiera estado a la mitad del jarro?

Soluci�n.
Examinando esta tarea nos asegurar�, que el modo de corneja, se acerca a la respuesta, pero no sobre cualquier nivel principal de agua en el jarro.
Para facilitar, admitiremos, que el jarro tiene la forma de una prisma rectangular, y pedruscos son unas pelotillas del mismo tama�o. Es f�cil de comprender, que el agua se sube sobre nivel de los pedruscos en aquel caso, cuando el ahorro del agua ocupa el mayor volumen, que espacio entre pedruscos: Luego el agua llenar� los espacios y saldr� por encima de pedruscos. Vamos a calcular cu�l volumen ocupan estos espacios. M�s f�cil hacer el calculo sobre aquella disposici�n de los pedruscos, cuando el centro de cada uno esta situado sobre una l�nea recta vertical con los centros de pelotillas de arriba y de abajo.
Sea d el di�metro de la pelotilla y por lo tanto, su volumen es 1/6 � p d ³ , el volumen c�bico inscrito a su alrededor d ³ . La diferencia de sus vol�menes d ³ - 1/6 p d ³ es el volumen de la parte vac�a del cubo, y la proporci�n es


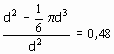
significa, que la parte vac�a de cada cubo forma 0,48 de su volumen. La misma parte, es decir un poco menos de la mitad, forma la suma de los vol�menes de todas vacuidades sobre el volumen del jarro. La cosa no se cambiara, si el jarro no tiene la forma prism�tica, y los pedruscos no tienen la forma esf�rica. En cualquier caso podemos afirmar, si principalmente el jarro lleno de agua al menos de la mitad, la corneja no podr� subir el nivel hasta los bordes, tir�ndole pedruscos.
Ser� la corneja mas fuerte, tanto, que era capaz de reducir al menor volumen y conseguir un estado compacto de los pedruscos, ella pudiera subir en dos veces mas, del nivel principal. Pero ella no es capaz de hacer esto, y permitiendo la colocaci�n friable de los pedruscos, nosotros estamos de acuerdo de acuerdo con las condiciones reales. Adem�s los jarros, habitualmente, en la parte del centro son m�s anchos; Esto tambi�n tiene que disminuir la subida de agua y se apoya nuestra conclusi�n correcta: Si el agua estaba mas bajo de la mitad, la corneja no ha podido tomar agua.
Volver