C O N T E N I D O
Pr�logo
1. Desayuno y rompecabezas
2. La matem�tica en el domin� y el croquet
3. Once rompecabezas m�s
4. �Sabe Usted Contar?
5. Rompecabezas num�ricos
6. Relatos de n�meros gigantes
7. Mediciones sin utilizar instrumentos
8. Rompecabezas de geometr�a
9. La geometr�a de la lluvia la nieve
10. Treinta problemas diferentes
Bajar parte 2
Escribir @ Antonio

Cap�tulo 10
Treinta problemas diferentes
Contenido:
86. La cadena
87. Las ararias y los escarabajos
88. El impermeable el sombrero y los chanclos
89. Los huevos de gallina y de pato
90. El vuelo
91. Regalos en met�lico
92. Las dos fichas
93. Con dos cifras
94. La unidad
95. Con cinco nueves
96. Con las diez cifras
97. Por cuatro procedimientos
98. Con cuatro unidades
99. Divisi�n enigm�tica
100. Un ejemplo m�s de divisi�n
101. �Qu� resulta?
102. Otro problema del mismo g�nero
103. El avi�n
104. Un mill�n de objetos
105. N�mero de caminos posibles
106. La esfera del reloj
107. La estrella de ocho puntas
108. La rueda con n�meros
109. La mesa de tres patas
110. Determinaci�n de �ngulos
111. Por el ecuador
112. En seis filas
113. �De qu� modo hacer la divisi�n?
114. El problema de Benediktov
Espero que la lectura de este libro no haya pasado sin dejar huella en el lector; que no s�lo le haya recreado, sino que le haya sido tambi�n de cierto provecho, desarrollando su comprensi�n e ingenio y ense��ndole a utilizar sus conocimientos con mayor decisi�n y soltura. El lector, seguramente, desear� comprobar su capacidad comprensiva. A este fin van destinadas las tres decenas de problemas de diverso g�nero, recopiladas en este �ltimo cap�tulo de nuestro libro.
86. La cadena
A un herrero le trajeron 5 trozos de cadena, de tres eslabones cada uno, y le encargaron que los uniera formando una cadena continua.
Antes de poner manos a la obra, el herrero comenz� a meditar sobre el n�mero de anillos que tendr�a necesidad de cortar y forjar de nuevo. Decidi� que le har�a falta abrir y cerrar cuatro anillos.
�No es posible efectuar este trabajo abriendo y enlazando un n�mero menor de anillos?
Soluci�n
Puede cumplirse el trabajo, abriendo s�lo tres eslabones. Para ello es preciso soltar los tres eslabones de uno de los trozos y unir con ellos los extremos de los cuatro trozos restantes.
Volver
87. Las ararias y los escarabajos
Un chiquillo caz� varias ara�as y escarabajos, en total ocho, y los guard� en una caja. Si se cuenta el n�mero total de patas que corresponde a los 8 animales resultan 54 patas.
�Cu�ntas ara�as y cu�ntos escarabajos hay en la caja?
Soluci�n
Para resolver este problema hay que recordar cu�ntas patas tiene un escarabajo y cu�ntas posee una ara�a. El escarabajo tiene 6 patas, la ara�a 8.
Sabiendo esto, supongamos que en la caja hubiera s�lo escarabajos. En este caso, el n�mero de patas ser�a 6 x 8 = 48, seis menos de las que se exigen en el problema. Reemplacemos un escarabajo por una ara�a. El n�mero de patas aumentar� en 2, puesto que la ara�a no tiene 6, sino 8 patas.
Est� claro que si hacemos esta operaci�n 3 veces consecutivas, el n�mero de patas llegar� a ser 54. Pero, entonces, de los 8 escarabajos quedar�n s�lo 5, los dem�s ser�n ara�as. As�, pues, en la caja hab�a 5 escarabajos y 3 ara�as. Hagamos la comprobaci�n: Los 5 escarabajos dan un total de 30 patas; las tres ara�as, 24, por tanto, 30 + 24 = 54, como exigen las condiciones planteadas en el problema.
Este problema puede resolverse tambi�n de otro modo. Supongamos que en la caja hubiera solamente ara�as. Entonces, el n�mero de patas ser�a 8 x 8 = 64, o sea diez m�s de las indicadas en el problema. Si reemplazamos una ara�a por un escarabajo, el n�mero de patas disminuir� en 2. Se necesita, por tanto, hacer 5 cambios semejantes para que el n�mero de patas llegue a ser el requerido, 54. En otras palabras, de las 8 ara�as hay que dejar s�lo 3 y las restantes reemplazarlas por escarabajos.
Volver
88. El impermeable el sombrero y los chanclos
Cierta persona compr� un impermeable, un sombrero y unos chanclos y pag� por todo 140 duros. El impermeable le cost� 90 duros m�s que el sombrero; el sombrero y el impermeable juntos costaron 120 duros m�s que los chanclos. �Cu�l es el precio de cada prenda?
El problema hay que resolverlo mentalmente, sin emplear ecuaciones.
Soluci�n
Si en lugar del impermeable, el sombrero y los chanclos, dicha persona hubiera comprado solamente dos pares de chanclos, en vez de 140 duros habr�a pagado tanto menos cuanto m�s baratos cuestan los chanclos que el impermeable y el sombrero juntos, o sea, 120 duros menos. Por tanto, los dos pares de chanclos costaron 140 - 120 = 20 duros.
Ahora ya sabemos que el impermeable y el sombrero juntos val�an 140 - 10 = 130 duros, y adem�s, que el impermeable costaba 90 duros m�s caro que el sombrero. Razonemos como lo hemos hecho antes: en lugar del impermeable y el sombrero, supongamos que esa persona comprara dos sombreros. Habr�a pagado, no 130 duros, sino 90 duros menos. Esto significa que los dos sombreros costaban 130 - 90 = 40 duros; de donde resulta que un sombrero val�a 20 duros.
Por consiguiente, el precio de las tres prendas fue: los chanclos, 10 duros; el sombrero, 20 duros, y el impermeable, 110 duros.
Volver
89. Los huevos de gallina y de pato
Las cestas que se ven en la figura contienen huevos; en unas cestas hay huevos de gallina, en las otras de pato. Su n�mero est� indicado en cada cesta. �Si vendo esta cesta -meditaba el vendedor, me quedar�n el doble de huevos de gallina que de pato.� �A qu� cesta se refiere el vendedor?

Soluci�n
El vendedor se refer�a a la cesta con 29 huevos. En las cestas con los n�meros 23, 12 y 5 hab�a huevos de gallina; los de pato se hallaban en las cestas designadas con el 14 y el 6.
Hagamos la comprobaci�n. Total de huevos de gallina que quedaron: 23 + 12 + 5 = 40. De pato 14 + 6 = 20.
De gallina hab�a el doble que de pato, lo que satisface las condiciones del problema.
Volver
90. El vuelo
Un avi�n cubri� la distancia que separa las ciudades A y B en 1 hora y 20 minutos. Sin embargo, al volar de regreso recorri� esa distancia en 80 minutos.
�C�mo se explica esto?
Soluci�n
En este problema no hay nada que aclarar. El avi�n tarda el mismo tiempo en hacer el vuelo en ambas direcciones, puesto que 80 minutos = 1 h y 20 minutos.
El problema va destinado exclusivamente a los lectores que no prestan la debida atenci�n al examinar las condiciones planteadas en �l y que pueden pensar que existe alguna diferencia entre 1 h 20 min y 80 min. Aunque parezca raro, son muchas las personas que no caen enseguida en la cuenta; su n�mero es mayor entre las acostumbradas a efectuar c�lculos, que entre las poco experimentadas en ese terreno. Se debe eso a la costumbre de emplear el sistema decimal y las unidades monetarias. Al ver la cifra 1 h 20 min y junto a ella 80 min, a primera vista nos parece como si existiera alguna diferencia entre ellas, como por ejemplo ocurre en el caso de 1 peseta 20 c�ntimos y 80 c�ntimos. Precisamente, el problema est� basado en este error psicol�gico del lector.
Volver
91. Regalos en met�lico
Dos padres regalaron dinero a sus hijos. Uno de ellos dio a su hijo ciento cincuenta duros, el otro entreg� al suyo cien. Result�, sin embargo, que ambos hijos juntos aumentaron su capital solamente en ciento cincuenta duros.�De qu� modo se explica esto?
Soluci�n
La clave del enigma consiste en que uno de los padres es hijo del otro. En total eran, no cuatro, sino tres personas: abuelo, hijo y nieto. El abuelo dio al hijo 150 duros y �ste, de ese dinero, entreg� al nieto (o sea, a su hijo) 100 duros, con lo cual los ahorros del hijo aumentaron, por consiguiente, s�lo en 50 duros.
Volver
92. Las dos fichas
En un tablero del juego de damas hay que colocar dos fichas, una blanca y otra negra. �De cu�ntos modos diferentes pueden disponerse dichas fichas?
Soluci�n
Una de las fichas puede colocarse en cualquiera de las 64 casillas, o sea, en 64 formas diferentes. Una vez colocada la primera, puede ponerse la segunda en cualquiera de las 63 casillas restantes. Por tanto, a cada una de las 64 posiciones de la primera ficha hay que a�adir las 63 posiciones de la segunda. En total, el n�mero de posiciones distintas que pueden ocupar las dos fichas en el tablero ser�:
Volver
93. Con dos cifras
�Cu�l es el menor n�mero entero positivo que puede usted escribir con dos cifras?
Soluci�n
El menor n�mero entero que puede escribirse con dos cifras no es el diez, como seguramente piensan algunos lectores, sino la unidad expresada de la manera siguiente:
Aquellos que conozcan el �lgebra pueden indicar tambi�n las siguientes:
puesto que cualquier n�mero elevado a cero es igual a la unidad.
Volver
94. La unidad
�C�mo expresar la unidad, empleando al mismo tiempo las diez primeras cifras?
Soluci�n
Hay que representarse la unidad como la suma de dos quebrados.
Los que tengan conocimientos de �lgebra pueden dar adem�s las siguientes respuestas:
etc�tera, pues los n�meros con exponente cero son iguales a la unidad.
Sin embargo, ser�a incorrecto que propusi�ramos como resoluci�n al problema 0 � 0 0 , pues estas expresiones no tienen significaci�n.
Volver
95. Con cinco nueves
Exprese el n�mero diez empleando cinco nueves. Indique, como m�nimo, dos procedimientos de los m�ltiples que hay para realizarlo.
Soluci�n
He aqu� dos procedimientos:
El que sepa �lgebra, puede aportar varias formas m�s, por ejemplo:
Volver
96. Con las diez cifras
Exprese el n�mero cien, utilizando las diez primeras cifras. �Por cu�ntos procedimientos puede usted hacerlo?
Soluci�n
He aqu� cuatro procedimientos:
Volver
97. Por cuatro procedimientos
Exprese el n�mero cien de cuatro modos distintos, empleando cinco cifras iguales.
Soluci�n
El n�mero 100 puede expresarse con cinco cifras iguales, empleando unos, treses, y lo m�s sencillo, cincos
Volver
98. Con cuatro unidades
�Cu�l es el n�mero mayor que puede usted escribir con cuatro unos?
Soluci�n
A esta pregunta se contesta con frecuencia: 1111. Sin embargo, puede formarse un n�mero mucho mayor: once elevado a la und�cima potencia, 11 11 . Si se tiene paciencia para llevar, hasta el fin esta operaci�n (con ayuda de los logaritmos estos c�lculos se efect�an mucho m�s r�pidamente), podr� uno ver que es superior a 280.000 millones. Por consiguiente, supera a 1111 m�s de 250 millones de veces.
Volver
99. Divisi�n enigm�tica
En el ejemplo de divisi�n que vamos a ver, todas las cifras est�n reemplazadas por asteriscos, a excepci�n de cuatro cuatros. Coloque en lugar de los asteriscos las cifras reemplazadas.
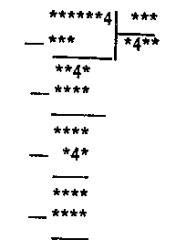
Este problema puede resolverse en diferentes formas.
Soluci�n
Los cuatro casos que damos a continuaci�n coinciden con el ejemplo de divisi�n propuesto:
1.343.784: 949 = 1.416
1.200.474: 846 = 1.419
1.202.464: 848 = 1.418
Volver
100. Un ejemplo m�s de divisi�n.
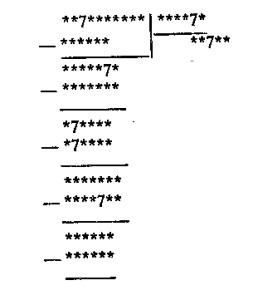
Soluci�n
Una manera de resolver este ejemplo es:
M�s tarde se han encontrado otros tres modos de resolverlo.
Estos dos �ltimos problemas, de dif�cil soluci�n, aparecieron por primera vez en las publicaciones norteamericanas Peri�dico de Matem�ticas, en el a�o 1920, y Mundo Escolar, en 1906.
Volver
101. �Qu� resulta?
Supongamos un cuadrado de un metro de lado, dividido en cuadraditos de un mil�metro. Calcule mentalmente qu� longitud se obtendr�a si coloc�semos todos los cuadraditos en l�nea, adosados unos a otros.
Soluci�n
En un metro cuadrado hay un mill�n de mil�metros cuadrados. Cada mil mil�metros cuadrados, dispuestos uno junto a otro, constituyen un metro; mil millares formar�n mil metros. Por lo tanto la l�nea formada tendr� un kil�metro de longitud.
Volver
102. Otro problema del mismo g�nero
Imag�nese un cubo de un metro de arista dividido en cubitos de un mil�metro. Calc�lense mentalmente los kil�metros de altura que tendr�a una columna formada por todos los cubitos dispuestos uno encima del otro.
Soluci�n
La respuesta asombra por la magnitud inesperada que se obtiene: la columna se eleva a 1.000 km.
Hagamos mentalmente el c�lculo. Un metro c�bico contiene 1.000 x 1.000 x 1.000 mil�metros c�bicos. Cada mil mil�metros c�bicos, colocados uno encima del otro, forman una columna de 1.000 m, o sea, 1 km. Pero como tenemos mil veces este n�mero de cubitos, la altura de la columna ser� de 1.000 km.
Volver
103. El avi�n
Un avi�n de doce metros de envergadura fue fotografiado desde el suelo durante su vuelo en el momento de pasar por la vertical del aparato. La c�mara fotogr�fica tiene doce cm de profundidad. En la foto, el avi�n presenta una envergadura de ocho mm. �A qu� altura volaba el avi�n en el momento de ser fotografiado?
Soluci�n

de donde x = 180 m.
Volver
104. Un mill�n de objetos
Un objeto pesa 89,4 g. Calcule mentalmente las toneladas que pesa un mill�n de estos objetos.
Soluci�n
Este tipo de c�lculo se efect�a mentalmente multiplicando 89,4 g por un mill�n, o sea, por mil millares.
Hagamos esta operaci�n multiplicando dos veces sucesivas por mil. 89,4 g x 1.000 = 89,4 kg, puesto que 1 kg es mil veces mayor que un gramo. Despu�s, 89,4 kg x 1.000 = 89,4 toneladas, pues una tonelada es mil veces mayor que un kilogramo. Por tanto, el peso buscado ser� 89,4 toneladas.
Volver
105. N�mero de caminos posibles
En la figura se ve un bosque dividido en sectores, separados entre s� por veredas. La l�nea de puntos indica el camino a seguir por las veredas para ir desde el punto A al B. Naturalmente, �ste no es el �nico camino entre dichos puntos, siguiendo las veredas. �Cu�ntos caminos diferentes, pero de igual longitud, existen entre los puntos mencionados?
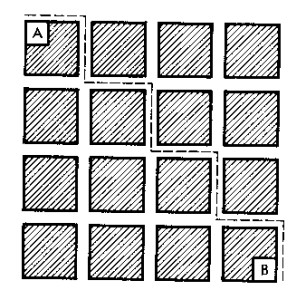
Soluci�n
El n�mero de caminos posibles para ir de A a B es de 70. (Este problema puede resolverse de forma sistem�tica utilizando el tri�ngulo de Pascal, que se describe en los libros de �lgebra.)
Volver
106. La esfera del reloj
Se trata de dividir esta esfera de reloj (v�ase la figura) en seis partes, de la forma que usted desee, pero con la condici�n de que en cada parte, la suma de los n�meros sea la misma.
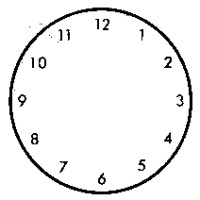
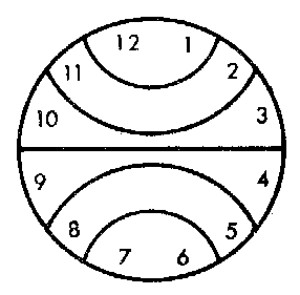
Este problema tiene por objeto comprobar m�s que su ingenio, su rapidez de comprensi�n.
Soluci�n
Como la suma de todas las cifras inscritas en la esfera del reloj es igual a 78, el n�mero correspondiente a cada parte deber� ser 78: 6 = 13. Esto facilita hallar la soluci�n que se muestra en la figura de la p�gina siguiente.
Volver
107. La estrella de ocho puntas
Hay que distribuir los n�meros del 1 al 16 en los puntos de intersecci�n de las l�neas de la figura de modo que la suma de los cuatro n�meros que se hallan en cada lado de los dos cuadrados sea 34 y que la suma de los cuatro n�meros que se encuentran en los v�rtices de cada cuadrado sea tambi�n 34.
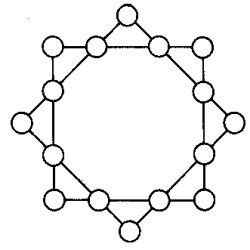
Soluci�n
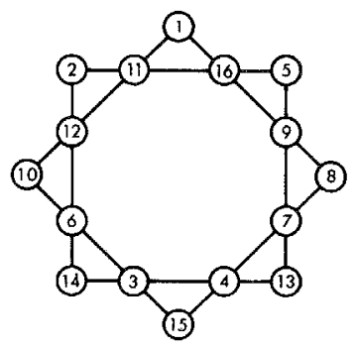
El modo de resolver estos problemas se indica en las figuras.
|
|
| Soluciones 107 y 108 | |
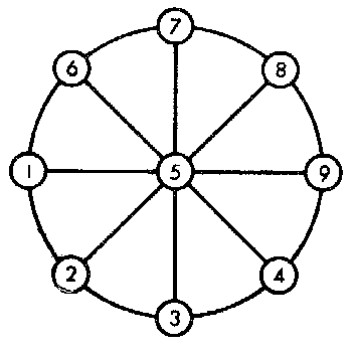
108. La rueda con n�meros
Las cifras del 1 al 9 hay que distribuirlas en la rueda de la figura: una cifra debe ocupar el centro del c�rculo y las dem�s, los extremos de cada di�metro de manera que las tres cifras de cada fila sumen siempre 15.
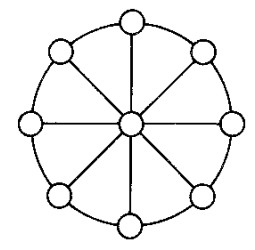
Volver
109. La mesa de tres patas
Existe la opini�n de que una mesa de tres patas nunca se balancea, incluso aunque las patas sean de longitud diferente. �Es verdad esto?
Soluci�n
Una mesa de tres patas siempre puede apoyarse correctamente en el suelo con los tres extremos de sus patas, puesto que por tres puntos situados en el espacio, puede pasar un plano y s�lo uno. Por este motivo, las mesas de tres patas son estables y nunca se balancean. Como se ve, este problema es puramente geom�trico y no f�sico.
He aqu� por qu� es muy c�modo emplear tr�podes para los instrumentos agrimensores y los aparatos fotogr�ficos' La cuarta pata no aumenta la estabilidad; por el contrario, habr�a siempre necesidad de preocuparse de la longitud exacta de las patas para que la mesa o los aparatos no se balancearan.
Volver
110. Determinaci�n de �ngulos
�Qu� magnitud tienen los �ngulos formados por las saetas de los relojes de la figura de la p�gina siguiente? Debe resolverse mentalmente sin utilizar el transportador.
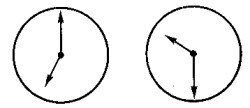
Soluci�n
Es f�cil contestar a la pregunta planteada en el problema si observamos la hora que marcan los relojes. Las agujas del reloj de la izquierda marcan las 7 en punto. Esto significa que los extremos de las agujas abarcan un arco equivalente a 5/12 de la circunferencia completa.
En grados, esto constituye:
Las agujas del reloj de la derecha marcan las nueve y media. El arco comprendido por sus extremos es 3 1/2 veces la duod�cima parte de la circunferencia, o sea 7/24 de �sta. Expresado en grados ser�:
360� * 7/24 = 105�
Volver
111. Por el ecuador
Si pudi�ramos recorrer la Tierra siguiendo el ecuador, la coronilla de nuestra cabeza describir�a una l�nea m�s larga que la planta de los pies. �Qu� magnitud tendr�a la diferencia entre estas longitudes?
Soluci�n
Supongamos que la persona tenga 175 cm de altura y designemos con la letra R el radio de la Tierra. Tendremos:
o sea, 11 metros. Lo sorprendente es que el resultado no depende en absoluto del radio del globo, y por tanto, es el mismo para el Sol que para una bolita.
Volver
112. En seis filas
Seguramente conoce usted la historia c�mica sobre c�mo nueve caballos fueron distribuidos en diez establos y en cada establo result� haber un caballo. El problema que voy a proponerle se parece mucho a esta broma c�lebre, pero no tiene soluci�n imaginaria, sino completamente real. Consiste en lo siguiente: Distribuir 24 personas en 6 filas de modo que en cada fila haya 5 personas.
Soluci�n
Las condiciones impuestas por el problema se satisfacen f�cilmente si colocamos las personas formando un hex�gono, como se muestra en la figura.

Volver
113. �De qu� modo hacer la divisi�n?
Existe un problema ya conocido: dividir una escuadra (o sea, un rect�ngulo del que se ha separado la cuarta parte) en cuatro partes iguales. Pruebe a dividir esta misma figura en tres partes, de manera que las tres sean iguales. �Es posible resolver este problema?
Soluci�n
El inter�s principal de este problema consiste en que para su resoluci�n no pueden tomarse magnitudes a, b, c, d, e, cualesquiera, sino que deber�n tener valores perfectamente determinados.
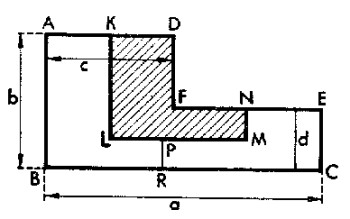
En efecto, queremos que la escuadra sombreada sea igual a cada una de las que no lo est�n. El lado LM es sin duda menor que BC; por lo tanto, deber� ser igual a AB. Por otra parte, LM debe ser igual a RC, o sea, LM = RC = b. Consiguientemente BR = a - z
Pero, BR debe ser igual a KL y CE, por lo tanto, BR = KL = CE, o sea, a - b = d y KL = d
De esto deducimos que a, b y d no pueden elegirse arbitrariamente. El lado d tiene que ser igual a la diferencia entre a y b. Pero esto es insuficiente. Veremos que todos los lados han de ser partes determinadas del lado a.
Evidentemente, tenemos que PR * KL = AB o PR * (a - b) = b, es decir, PR = 2b - a. Comparando los lados correspondientes de las escuadras, la sombreada y la no sombreada de la derecha, obtendremos: PR = MN, es decir, PR = d/2 de donde d/2 = 2b - a.
Si comparamos esta �ltima igualdad con la a - b = d, veremos que b = 3/5 a y d = 2/5 a.
Confrontando la figura sombreada y la de la izquierda de las no sombreadas vemos tambi�n que AK = MN, o sea, AK = PR = d/2 = 1/5 a. En esta forma nos convencemos que KD = PR = 1/5 a; por consiguiente, AD = 2/5 a.
Volver
114. El problema de Benediktov
Muchos conocedores de la literatura universal no sospechan que el poeta V. Benediktov es autor de la primera colecci�n en ruso de rompecabezas matem�ticos. Este compendio no fue publicado; qued� en forma de manuscrito y no fue descubierto hasta 1924. Tuve la posibilidad de conocerlo, e incluso llegu� a establecer el a�o 1869 como fecha en que fue escrito (en el manuscrito no se se�ala), bas�ndome en uno de los rompecabezas.
Copio de ese compendio el siguiente problema, expuesto por el poeta en forma literaria. Se titula Soluci�n ingeniosa de un problema complicado:
Una comadre ten�a para vender nueve decenas de huevos. Envi� al mercado a sus tres, hijas, entregando a la mayor y m�s lista de ellas una decena; a la segunda, tres decenas, y a la tercera, la menor, cincuenta huevos, y les dijo:
-Poneos previamente de acuerdo y fijad el precio a que deb�is vender los huevos, y no os volv�is atr�s de lo convenido. Manteneos firmes las tres en lo tocante al precio; pero conf�o en que mi hija mayor, gracias a su sagacidad, aun ateni�ndose al acuerdo de vender todas al mismo precio, sacar� tanto por su decena como la segunda por sus tres decenas, y al mismo tiempo, aleccionar� a la segunda hermana sobre c�mo vender las tres decenas por el mismo precio que la menor los cincuenta huevos. El producto de la venta y el precio deben ser los mismos para las tres. Quiero que vend�is todos los huevos, de modo que saquemos, en n�meros redondos, 10 kopeks, como m�nimo, por cada decena y no menos de 90 kopeks por las nueve decenas.
Con esto interrumpo, por ahora, el relato de Benediktov, a fin de que los propios lectores puedan adivinar c�mo cumplieron las tres muchachas el encargo recibido.
Soluci�n
Continuemos el cuento de Benediktov, que qued� interrumpido:
La tarea era complicada. Las hijas, camino del mercado, comenzaron a consultarse una a la otra. La segunda y la tercera recurrieron al ingenio de la mayor, pidi�ndole consejo. �sta, despu�s de pensar el asunto, dijo:
-Hermanas, vamos a vender los huevos estableciendo el precio, no por docenas, como ven�amos haciendo hasta ahora, sino por septenas y ese precio lo mantendremos firmemente como nos indic� nuestra madre. �No rebaj�is ni un kopek el precio convenido! Por la primera septena pediremos 3 kopeks, �de acuerdo?
-�Tan barato! -exclam� la segunda.
-S�, pero en cambio -contest� la mayor-, subiremos el precio para los huevos sueltos que quedan en las cestas despu�s de vender todas las septenas posibles. Me he enterado de que no habr� en el mercado m�s vendedoras de huevos que nosotras tres. No habr�, por tanto, competencia en el precio. Es sabido que cuando la mercanc�a est� termin�ndose y hay demanda, los precios suben. Con los huevos restantes recuperaremos las p�rdidas.
-�Y qu� precio vamos a pedir por los restantes? -pregunt� la peque�a.
-Nueve kopeks por cada huevo, y s�lo este precio. Al que le hagan mucha falta huevos los pagar�, no te preocupes.
-�Pero es muy caro! -repuso la segunda hermana.
-�Y qu�? -respondi� la mayor-; los primeros huevos, vendidos por septenas, son baratos. Lo uno compensar� a lo otro.
Llegaron al mercado y cada una de las hermanas se sent� en sitio diferente. Comenzaron a vender. Los compradores, contentos con la baratura, lanz�ronse al puesto de la hermana menor, que ten�a cincuenta huevos, y se los compraron en un abrir y cerrar de ojos. Vendi� siete septenas, y obtuvo 21 kopeks. En la cesta le qued� un huevo. La segunda, que ten�a tres decenas, vendi� 28 huevos, o sea, 4 septenas, y le quedaron 2 huevos. Sac� de beneficio 12 kopeks. La mayor vendi� una septena, sac� 3 kopeks y le quedaron 3 huevos.
Inesperadamente se present� en el mercado una cocinera, enviada por su ama a comprar sin falta, costara lo que costara, una docena de huevos. Para pasar unos d�as con la familia, hab�an llegado los hijos de la se�ora, que gustaban extraordinariamente de los huevos fritos. La cocinera corr�a de un lado para otro, pero los huevos ya se hab�an terminado. A las tres �nicas vendedoras que hab�a en el mercado les quedaban s�lo 6 huevos: a una, un huevo, a otra, dos, y a la tercera, tres.
-�Vengan ac� esos huevos! -dijo.
La cocinera se acerc� primero a la que ten�a 3 huevos, la hermana mayor, que como sabemos hab�a vendido una septena por 3 kopeks.
La cocinera pregunt�:
-�Cu�nto quieres por los tres huevos? -Nueve kopeks por cada uno.
-�Qu� dices? �Te has vuelto loca? -pregunt� la cocinera. -Como usted quiera -contest�-, pero a menor precio no los doy. Son los �ltimos que me quedan.
La cocinera se acerc� a la otra vendedora, que ten�a 2 huevos en la cesta.
-�Cu�nto cuestan?
-A 9 kopeks. Es el precio establecido. Ya se terminan. -�Y tu huevo, cu�nto vale? -pregunt� la cocinera a la hermana menor.
-Lo mismo: 9 kopeks.
�Qu� hacer! No tuvo m�s remedio que comprarlos a este precio inaudito.
-Venga, compro todos los huevos que quedan.
La cocinera dio a la hermana mayor 27 kopeks por los tres huevos, que con los tres kopeks que ten�a, sumaban treinta; a la segunda le entreg� 18 kopeks por el par de huevos, que con los 12 que hab�a cobrado antes constitu�an 30 kopeks. La peque�a recibi� de la cocinera, por el �nico huevo que le quedaba, 9 kopeks que al juntarlos con los 21 que ya pose�a, le resultaron tambi�n 30 kopeks.
Terminada la venta, las tres hijas regresaron a casa, y al entregar cada una 30 kopeks a su madre, le contaron c�mo hab�an vendido los huevos, manteniendo todas un precio fijo y �nico y c�mo se las hab�an arreglado para que la ganancia, correspondiente a una decena y a cincuenta huevos, resultara una misma cantidad y en total 90 kopeks.
Volver