Cap�tulo 3
Once rompecabezas m�s

Contenido:
25. El bramante
26. Calcetines y guantes
27. La longevidad del cabello
28. El salario
29. Carrera de esqu�es
30. Dos obreros
31. Copia de un informe
32. Dos ruedas dentadas
33. �Cu�ntos a�os tiene?
34. �Cu�ntos a�os tiene Roberto?
35. De compras



25. El bramante
-�M�s cordel? - pregunt� la madre, sacando las manos de la tina en que lavaba. Ayer mismo te di un buen ovillo. �Para qu� necesitas tanto? �D�nde lo has metido?
-�D�nde lo he metido? - contest� el muchacho -. Primero me cogiste la mitad...
-�Con qu� quieres que ate los paquetes de ropa blanca?
-La mitad de lo que qued� se la llev� Tom para pescar.
-Debes ser condescendiente con tu hermano mayor.
-Lo fui. Qued� muy poquito y de ello cogi� pap� la mitad para arreglarse los tirantes que se te hab�an roto de tanto re�rse con el accidente de autom�vil. Luego, Mar�a necesit� dos quintos del resto, para atar no s� qu�...
-�Qu� has hecho con el resto del cordel?
-�Con el resto? �No quedaron m�s que 30 cm!
-�Qu� longitud ten�a el cordel al principio?

Soluci�n
Despu�s de haber cogido la madre la mitad, qued� 1/2; despu�s de cederle al hermano mayor, 1/4; despu�s de haber cortado el padre, 1/8 y despu�s de la hermana, 1/8 * 3/5 * = 3/40. Si 30 cm constituyen los 3/40 de la longitud inicial del bramante, la longitud total equivaldr� a 30/(3/40) cm; o sea, 4 m.
Volver

26. Calcetines y guantes
En una misma caja hay diez pares de calcetines color caf� y diez pares negros, y en otra caja hay diez pares de guantes caf� y otros tantos pares negros. �Cu�ntos calcetines y guantes es necesario sacar de cada caja, para conseguir un par de calcetines y un par de guantes de un mismo color (cualquiera)?

Soluci�n
Bastan tres calcetines, porque dos ser�n siempre del mismo color. La cosa no es tan f�cil con los guantes, que se distinguen no s�lo por el color, sino porque la mitad de los guantes son de la mano derecha y la otra mitad de la izquierda. En este caso har� falta sacar 21 guantes. Si se sacan menos, por, ejemplo 20, puede suceder que los 20 sean de una mano (por ejemplo, 10 de color caf� de la mano izquierda y 10 negros de la izquierda).
Volver

27. La longevidad del cabello
�Cu�ntos cabellos hay por t�rmino medio en la cabeza de una persona? Se han contado unos 150.000. Se ha determinado tambi�n que mensualmente a una persona se te caen cerca de 3.000 pelos.
�C�mo calcular cu�nto tiempo dura en la cabeza cada pelo?

Soluci�n
Est� claro que el pelo que tarda m�s en caer es el m�s reciente, es decir, el que tiene un d�a de edad.
Veamos al cabo de cu�nto tiempo le llegar� el turno de caerse. De los 150.000 pelos que hay, en un momento dado, en la cabeza, durante el primer mes caen 3.000; los dos primeros meses, 6.000; en el curso del primer a�o, 12 veces 3.000, o sea, 36.000. Por consiguiente pasar�n poco m�s de cuatro a�os antes de que al �ltimo pelo le llegue el turno de caerse.
Volver

28. El salario
La �ltima semana he ganado 250 duros, incluyendo el pago por horas extraordinarias. El sueldo asciende a 200 duros m�s que lo recibido por horas extraordinarias. �Cu�l es mi salario sin las horas extraordinarias?

Soluci�n
Sin pensarlo, muchos contestan: 200 duros. No es as�, porque en ese caso el salario fundamental ser�a s�lo 150 duros m�s que lo cobrado por horas extraordinarias, y no 200 duros m�s.
El problema hay que resolverlo del modo siguiente. Sabemos que si sumamos 200 duros a lo cobrado por horas extraordinarias, nos resulta el salario fundamental. Por eso, si a 250 duros les sumamos 200 duros deben resultarnos dos salarios fundamentales. Pero 250 + 200 = 450. Esto es, 450 duros constituyen dos veces el salario fundamental. De aqu� que un salario fundamental, sin el pago por horas extraordinarias, equivalga a 225 duros; lo correspondiente a las horas extraordinarias es lo que falta hasta 250 duros, es decir, 25 duros.
Hagamos la prueba: el salario fundamental -225 duros- sobrepasa en 200 -duros lo cobrado por las horas extraordinarias, 25 duros, de acuerdo con las condiciones del problema.
Volver

29. Carrera de esqu�es
Un esquiador calcul� que si hac�a 10 km por hora, llegar�a al sitio designado una hora despu�s del mediod�a; si la velocidad era de 15 km por hora, llegar�a una hora antes del mediod�a.
�A qu� velocidad debe correr para llegar al sitio exactamente al mediod�a?

Soluci�n
Este problema es curioso por dos razones: en primer lugar puede sugerir la idea de que la velocidad buscada es la media entre 10 y 15 km por hora; es decir, igual a 12 112 kil�metros por hora. No es dif�cil convencerse de la falsedad de esa suposici�n. Efectivamente, si la distancia del recorrido es a kil�metros, el esquiador, yendo a una velocidad de 15 km por hora, estar� en camino a/15 horas; y si lo hace a 10 km/h, a/10; recorri�ndolo a 12,5 km/h, estar� a/(12,5) o sea 2a/25 horas. Pero entonces debe establecerse la igualdad:

2a /25 - a/15 = a/10 - 2*a /25
porque cada una de estas diferencias equivale a una hora. Reduciendo a en todos los numeradores tendremos:

2/25 - 1/15 = 1/10 - 2/25
pasando de un miembro a otro de la igualdad y sumando, resulta:

5/25 = 1/15 + 1/10
igualdad falsa, pues

1/15 + 1/10 = 1/6, es decir, 4/24 y no 4/25
La segunda particularidad del problema es que puede resolverse, no s�lo sin ayuda de ecuaciones, sino por c�lculo mental.
Hagamos el siguiente razonamiento: si el esquiador, a la velocidad de 15 km por hora, estuviera en camino dos horas m�s (es decir, tantas como haciendo el recorrido a 10 km por hora), recorrer�a 30 km m�s de los que recorri� en realidad. Sabemos que en una hora cubre 5 km m�s; estar�a, pues, en camino 30/5 = 6 horas. De aqu� que la carrera durar� 6 - 2 = 4 horas, marchando a 15 km por hora. Y a su vez se averigua la distancia recorrida: 15 x 4 = 60 kil�metros.
Ahora es f�cil averiguar a qu� velocidad debe marchar el esquiador para llegar a la meta al mediod�a en punto; en otras palabras, para emplear 5 horas en el recorrido.
60/ 5 = 12 km.
Pr�cticamente puede comprobarse con facilidad que la soluci�n es exacta.
Volver

30. Dos obreros
Dos obreros, uno viejo y otro joven, viven en un mismo apartamento y trabajan en la misma f�brica. El joven va desde casa a la f�brica en 20 minutos; el viejo, en 30 minutos. �,En cu�ntos minutos alcanzar� el joven al viejo, andando ambos a su paso normal, si �ste sale de casa 5 minutos antes que el joven?

Soluci�n
El problema puede resolverse, sin recurrir a las ecuaciones, por diversos procedimientos.
He aqu� el primero: El obrero joven recorre en 5 minutos 1/4 del camino, el viejo 1/6, es decir, menos que el joven en 1/4 - 1/6= 1/12
Como el viejo hab�a adelantado al joven en 1/6 del camino, el joven lo alcanzar� a los (1/6) / (1/12) = 2 espacios de cinco minutos; en otras palabras, a los 10 minutos.
Otro m�todo m�s sencillo. Para recorrer todo el camino, el obrero viejo emplea 10 minutos m�s que el joven. Si el viejo saliera 10 minutos antes que el joven, ambos llegar�an a la f�brica a la vez. Si el viejo ha salido s�lo 5 minutos antes, el joven debe alcanzarle precisamente a mitad de camino; es decir, 10 minutos despu�s (el joven recorre todo el camino en 20 minutos).
Son posibles otras soluciones aritm�ticas.
Volver

31. Copia de un informe
Encarg�se a dos mecan�grafas que copiaran un informe. La que escrib�a m�s r�pidamente hubiera podido cumplir el encargo en 2 horas; la otra, en 3 horas.
�En cu�nto tiempo copiar�n ambas ese informe, si se distribuyen el trabajo para hacerlo en el plazo m�s breve posible?
Problemas de este tipo se resuelven generalmente por el m�todo de los conocidos problemas de dep�sitos. 0 sea: en nuestro problema, se averigua qu� parte del trabajo realiza en una hora cada mecan�grafa; se suman ambos quebrados y se divide la unidad por esta suma. �No podr�a usted discurrir un m�todo diferente, nuevo, para resolver problemas semejantes?

Soluci�n
Ante todo, hagamos la pregunta: �c�mo deben las mecan�grafas repartiese el trabajo para terminarlo a la vez? (Es evidente que el encargo podr� ser ejecutado en el plazo m�s breve s�lo en el caso de que no haya interrupciones.) Como la mecan�grafa m�s experimentada escribe vez y media m�s r�pidamente que la de menos experiencia, es claro que la parte que tiene que escribir la primera debe ser vez y media mayor que la de la segunda, y entonces ambas terminar�n de escribir al mismo tiempo. De aqu� se deduce que la primera deber� encargarse de copiar 3/5 del informe y la segunda 2/5.
En realidad el problema est� ya casi resuelto. S�lo queda averiguar en cu�nto tiempo la primera mecan�grafa realizar� los 3/5 de su trabajo. Puede hacer todo su trabajo, seg�n sabemos, en 2 horas; es decir, que lo har� en 2 * 3/5 = 1 1/5 horas. En el mismo tiempo debe realizar su trabajo la segunda mecan�grafa.
As� pues, el espacio de tiempo m�s breve durante el cual pueden ambas mecan�grafas copiar el informe es 1 hora 12 minutos.
Volver

32. Dos ruedas dentadas
Un pi��n de 8 dientes est� engranado con una rueda dentada de 24 dientes (v�ase la figura). Al dar vueltas la rueda grande, el pi��n se mueve por la periferia.



�Cu�ntas veces girar� el pi��n alrededor de su eje, mientras da una vuelta completa alrededor de la rueda dentada grande?

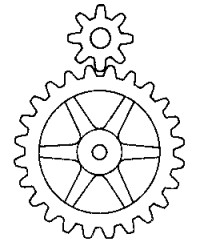
Soluci�n
Si piensa usted que el pi��n girar� tres veces, se equivoca: dar� cuatro vueltas y no tres.
Para ver claramente c�mo se resuelve el problema, ponga en una hoja lisa de papel dos monedas iguales, por ejemplo de una peseta, como indica la figura. Sujetando con la mano la moneda de debajo, vaya haciendo rodar por el borde la de arriba. Observar� una cosa inesperada: cuando la moneda de arriba haya recorrido media circunferencia de la de abajo y quede situada en su parte inferior, habr� dado la vuelta completa alrededor de su eje. Esto puede comprobarse f�cilmente por la posici�n de la cifra de la moneda. Al dar la vuelta completa a la moneda fija, la m�vil tiene tiempo de girar no una vez, sino dos veces.
Al girar un cuerpo trazando una circunferencia, da siempre una revoluci�n m�s que las que pueden contarse directamente. Por ese motivo, nuestro globo terrestre, al girar alrededor del Sol, da vueltas alrededor de su eje no 365 veces y 1/4, sino 366 y 1/4, si consideramos las vueltas en relaci�n con las estrellas y no en relaci�n con el Sol. Ahora comprender� usted por qu� los d�as siderales son m�s cortos que los solares.
Volver

33. �Cu�ntos a�os tiene?
A un aficionado a los rompecabezas le preguntaron cu�ntos a�os ten�a. La contestaci�n fue compleja:
-Tomad tres veces los a�os que tendr� dentro de tres a�os, restadles tres veces los a�os que ten�a hace tres a�os y resultar� exactamente los a�os que tengo ahora. �Cu�ntos a�os tiene?

Soluci�n
La soluci�n aritm�tica es bastante complicada, pero el problema se resuelve con facilidad si recurrimos al �lgebra y planteamos una ecuaci�n. Designaremos con la letra x el n�mero de a�os buscado. La edad tres a�os despu�s se expresar� por x + 3, y la edad de 3 antes por x - 3. Tenemos la ecuaci�n:

3 (x + 3) - 3 (x - 3) = x.
Despejando la inc�gnita, resulta x = 18. El aficionado a los rompecabezas tiene ahora 18 a�os.
Comprob�moslo: Dentro de tres a�os tendr� 21; hace tres a�os, ten�a s�lo 15. La diferencia

3 * 21 - 3 * 15 = 63 - 45 = 18
es decir, igual a la edad actual.
Volver

34. �Cu�ntos a�os tiene Roberto?
-Vamos a calcularlo. Hace 18 a�os, recuerdo que Roberto era exactamente tres veces m�s viejo que su hijo.
-Espere; precisamente ahora, seg�n mis noticias, es dos veces m�s viejo que su hijo.
-Y por ello no es dif�cil establecer cu�ntos a�os tienen Roberto y su hijo.
�Cu�ntos?

Soluci�n
Como el problema anterior, �ste se resuelve con una sencilla ecuaci�n. Si el hijo tiene ahora x a�os, el padre tiene 2x. Hace 18 a�os, cada uno ten�a 18 menos: el padre 2x - 18, el hijo x - 18. Se sabe que entonces el padre era tres veces m�s viejo que el hijo:
3 (x - 18) = 2x - 18
Despejando la inc�gnita nos resulta x = 36; el hijo tiene 36 a�os y el padre 72.
Volver

35. De compras
Al salir de compras de una tienda de Par�s, llevaba en el portamonedas unos 15 francos en piezas de un franco y piezas de 20 c�ntimos. Al regresar, tra�a tantos francos como monedas de 20 c�ntimos ten�a al comienzo, y tantas monedas de 20, c�ntimos como piezas de franco ten�a antes. En el portamonedas me quedaba un tercio del dinero que llevaba al salir de compras.
�Cu�nto costaron las compras?

Soluci�n
Designemos el n�mero inicial de francos sueltos por x, y el n�mero de monedas de 20 c�ntimos por y. Al salir de compras, yo llevaba en el portamonedas:
(100x + 20y) c�ntimos.
Al regresar ten�a:
(100y + 20x) c�ntimos.
Sabemos que la �ltima suma es tres veces menor que la primera; por consiguiente:
3 (100y + 20x) = 100x + 20y.
Simplificando esta expresi�n, resulta:
x = 7y.
Para y = 1, x es igual a 7. Seg�n este supuesto, yo ten�a al comienzo 7 francos 20 c�ntimos; lo que no est� de acuerdo con las condiciones del problema (�unos 15 francos�).
Probemos y = 2; entonces x = 14. La suma inicial era igual a 14 francos 40 c�ntimos, lo que satisface las condiciones del problema.
El supuesto y = 3 produce una suma demasiado grande: 21 francos 60 c�ntimos.
Por consiguiente, la �nica contestaci�n satisfactoria es 14 francos 40 c�ntimos. Despu�s de comprar, quedaban 2 francos sueltos y 14 monedas de 20 c�ntimos, es decir, 200 + 280 = 480 c�ntimos; esto, efectivamente, es un tercio de la suma inicial (1.440 : 3 = 480).
Lo gastado ascendi� a 1.440 - 480 = 960. 0 sea, que el coste de las compras fue 9 francos 60 c�ntimos.
Volver