C O N T E N I D O
Pr�logo
1. Desayuno y rompecabezas
2. La matem�tica en el domin� y el croquet
3. Once rompecabezas m�s
4. �Sabe Usted Contar?
5. Rompecabezas num�ricos
6. Relatos de n�meros gigantes
7. Mediciones sin utilizar instrumentos
8. Rompecabezas de geometr�a
9. La geometr�a de la lluvia la nieve
10. Treinta problemas diferentes
Bajar parte 2
Escribir @ Antonio

Cap�tulo 5
Rompecabezas num�ricos
Contenido:
38. Por cinco francos, cien
39. Un millar
40. Veinticuatro
41. Treinta
42. Las cifras que faltan
43. �Qu� n�meros son?
44. �Qu� n�mero hemos dividido?
45. Divisi�n por 11
46. Casos singulares de multiplicaci�n
47. Tri�ngulo num�rico
48. Otro tri�ngulo num�rico
49. Estrella m�gica
38. Por cinco francos, cien
Un artista de variedades, en un circo parisiense, hac�a al p�blico esta seductora proposici�n:
-Declaro ante testigos que pagar� 100 francos al que me d� cinco francos en veinte monedas; deber� haber, entre estas 20, tres clases de monedas: de 50 c�ntimos, de 20 c�ntimos y de 5 c�ntimos. �Cien francos por cinco! �Qui�n los desea?
Rein� el silencio. El p�blico qued� sumido en reflexiones. Los l�pices corr�an por las hojas de las libretas de notas; pero nadie aceptaba la propuesta.
-Estoy viendo que el p�blico considera que 5 francos es un precio demasiado elevado para un billete de 100 francos. Bien; estoy dispuesto a rebajar dos francos y a establecer un precio menor: 3 francos, en monedas, del valor indicado. �Pago 100 francos, por 3! �Que se pongan en cola los que lo deseen!
Pero no se form� cola. Estaba claro que el p�blico vacilaba en aprovecharse de aquel caso extraordinario.
-�Es que 3 francos les parecen tambi�n mucho? Bien, rebajo un franco m�s. Abonen, en las indicadas monedas, s�lo 2 francos, y entregar� cien francos al que lo haga.
Como nadie se mostrara dispuesto a realizar el cambio, el artista continu�:
-�Quiz� no tengan ustedes dinero suelto! No se preocupen, pueden entreg�rmelo m�s tarde. �Denme s�lo escrito en un papel cu�ntas monedas de cada clase se comprometen a traer!
Por mi parte, estoy dispuesto a pagar tambi�n cien francos a todo lector que me env�e por escrito la lista correspondiente.
Soluci�n
Ninguno de los tres problemas (36, 37 y 38) tiene soluci�n y tanto el artista como yo hemos podido sin riesgo alguno prometer cualquier premio por la soluci�n de los mismos. Para convencerse de ello, recurramos al �lgebra.
Pagando 5 francos. Supongamos que sea posible y que para hacerlo han hecho falta x monedas de 50 c�ntimos, y de 20 c�ntimos y z de 5. Tendremos la ecuaci�n:
Dividiendo todos los t�rminos por 5, resulta:
Adem�s, como el n�mero total de monedas, seg�n las condiciones del problema, equivale a 20, se puede formar otra ecuaci�n con los n�meros x, y, z.x + y + z = 20Restando esta ecuaci�n de la que hemos obtenido antes nos resulta:
Dividiendo por 3, tenemos:
Pero 3x -tres veces el n�mero de monedas de 50 c�ntimos- es un n�mero entero. El n�mero de monedas de 20 c�ntimos -y- es asimismo un n�mero entero. La suma de dos enteros no puede ser nunca un n�mero mixto (26 2/3). Nuestro supuesto de que el problema ten�a soluci�n nos lleva, como se ve, al absurdo. El problema, pues, no tiene soluci�n.
El lector, siguiendo este procedimiento, se convence de que los otros dos problemas despu�s de la rebaja -abonando 3 y 2 francos- tampoco tienen soluci�n. El primero nos lleva a la ecuaci�n:
y el segundo a:
Ambos son insolubles, pues deben ser expresados en n�meros enteros.
Como ve usted, el artista no arriesgaba nada al ofrecer importantes sumas por la soluci�n de estos problemas: nunca habr� de entregar los premios ofrecidos.
Otra cosa ser�a si se propusiera abonar, por ejemplo, 4 francos a base de las 20 monedas del tipo indicado, en vez de 5, 3 o 2.
El problema se resolver�a f�cilmente por siete procedimientos distintos. He aqu� una de las posibles soluciones: 6 monedas de 50 c�ntimos, 2 de 20 c�ntimos y 12 de 5 c�ntimos.
Volver
39. Un millar
�Puede usted expresar el n�mero 1.000 utilizando ocho cifras iguales? (Adem�s de las cifras se permite utilizar tambi�n los signos de las operaciones.)
Soluci�n
Volver
40. Veinticuatro
Es f�cil expresar el n�mero 24 por medio de tres ochos: 8 + 8 + 8. �Podr� hacerse esto mismo utilizando no el ocho, sino otras tres cifras iguales? El problema tiene m�s de una soluci�n.
Soluci�n
Volver
41. Treinta
El n�mero 30 es f�cil expresarle con tres cincos: 5 x 5 + 5. Es m�s dif�cil hacer esto mismo con otras tres cifras iguales. Pru�belo. �No lograr�an encontrar varias soluciones?
Soluci�n
Indicamos tres soluciones:
33 - 3 = 30
Volver
42. Las cifras que faltan
En la siguiente multiplicaci�n, m�s de la mitad de las cifras est�n sustituidas por asterisco.
�Podr�a reponer las cifras que faltan?

Soluci�n
Las cifras que faltan se restablecen poco a poco, utilizando el siguiente m�todo deductivo:Para mayor comodidad numeremos las filas:
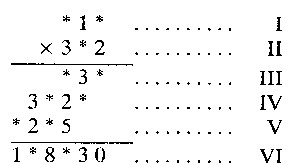
Es f�cil determinar que el �ltimo asterisco de la l�nea III es un 0; se ve claramente, por ser tambi�n un 0 la �ltima cifra de la fila VI.
A continuaci�n se determina el valor del �ltimo asterisco de la fila 1; es una cifra que multiplicada por 2, da un n�mero que termina en 0, y al multiplicarla por 3 da un n�mero terminado en 5 (fila V). El 5 es la �nica cifra posible.
No es dif�cil adivinar qu� se oculta tras el asterisco de la fila II: un 8, porque s�lo al multiplicar este n�mero por el 15 da de producto un n�mero terminado en 20 como el que tenemos (fila IV).
Finalmente, est� claro el valor del primer asterisco de la fila I: es 4, porque s�lo este n�mero multiplicado por 8 da un producto que empieza por 3 (fila IV).
No presenta dificultad alguna averiguar las restantes cifras desconocidas: basta multiplicar los n�meros de las dos primeras filas, determinados ya.
Resulta la multiplicaci�n siguiente:
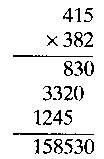
Volver
43. �Qu� n�meros son?
He aqu� otro problema del mismo tipo. Se pide la reposici�n de los n�meros en la multiplicaci�n siguiente:
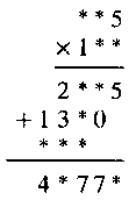
Soluci�n
El valor que sustituye los asteriscos en este problema se averigua siguiendo un procedimiento deductivo semejante al que ya hemos utilizado para la resoluci�n de� problema anterior.
Resulta:
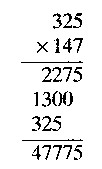
Volver
44. �Qu� n�mero hemos dividido?
Repongan las cifras que faltan en la divisi�n:
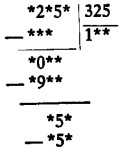
Soluci�n
He aqu� la divisi�n que se buscaba:
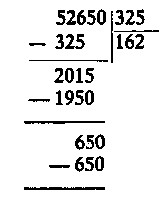
Volver
45. Divisi�n por 11
Escriba un n�mero de 9 cifras, sin que se repita ninguna de ellas (es decir, que todas las cifras sean diferentes), y que sea divisible por 11.
Escriba el mayor de todos los n�meros que satisfaga estas condiciones.
Escriba el menor de todos ellos.
Soluci�n
Para resolver este problema hay que saber en qu� casos es un n�mero divisible por 11. Un n�mero es divisible por 11 si la diferencia entre la suma de los valores absolutos de las cifras colocadas en los lugares pares y la suma de los valores de las colocadas en los lugares impares, es divisible por 11 o igual a cero.
Por ejemplo, hagamos la prueba con el n�mero 23.658.904. La suma total de las cifras colocadas en los lugares pares es:
La suma de las cifras colocadas en los lugares impares es:
La diferencia entre estas sumas (hay que restar del n�mero mayor el menor) es:
Esta diferencia (5) no se divide por 11, lo que quiere decir que el n�mero no es divisible por 11.
Probemos el n�mero 7.344.535:
Como el 11 se divide por 11, el n�mero que hemos probado es m�ltiplo de 11.
Ahora ya nos es f�cil determinar en qu� orden hay que escribir las nueve cifras para que resulte un m�ltiplo de 11 y para satisfacer lo que el problema exige. Por ejemplo: 352.049.786.
Hagamos la prueba:
La diferencia es 22 - 22 = 0; quiere decirse que el n�mero indicado es m�ltiplo de 11.
El mayor de todos los n�meros pedidos es:
Y el menor:
Volver
46. Casos singulares de multiplicaci�n
F�jese en est� multiplicaci�n de dos n�meros:
48 x 159 = 7.632
En ella participan las 9 cifras significativas.
�Podr�a usted encontrar algunos otros ejemplos semejantes? En caso afirmativo, �cu�ntos hay?
Soluci�n
Un lector paciente puede encontrar nueve casos distintos de esta clase de multiplicaci�n. Son los siguientes:
42 x 138 = 5.796
18 x 297 = 5.346
27 x 198 = 5.346
39 x 186 = 7.254
48 x 159 = 7.632
28 x 157 = 4.396
4 x 1.738 = 6.952
4 x 1.963 = 7.852
Volver
47. Tri�ngulo num�rico
En los circulitos de este tri�ngulo (v�ase la figura) coloque las nueve cifras significativas en forma tal que la suma de cada lado sea 20.
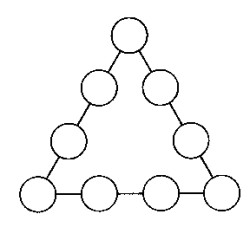
Soluci�n 47 y 48
Las figuras muestran las soluciones. Las cifras del centro de cada fila pueden permutarse entre s� y de ese modo se obtienen algunas soluciones m�s.
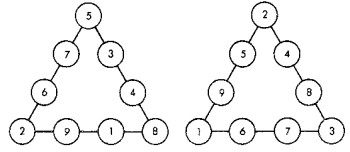
Volver
48. Otro tri�ngulo num�rico
Hay que distribuir las cifras significativas en los c�rculos del mismo tri�ngulo (v�ase la figura) de modo que la suma en cada lado sea 17.
Volver
49. Estrella m�gica
La estrella num�rica de seis puntas dibujada en la figura tiene una propiedad m�gica: las seis filas de n�meros dan una misma suma:
|
4+6+ 7+9=26
4+8+12+2=26 9+5+10+2=26 |
11+ 6+ 8+1=26
11+ 7+ 5+3=26 1 + 12 + 10 + 3 = 26 |
La suma de los n�meros colocados en las puntas de la estrella,
es diferente:
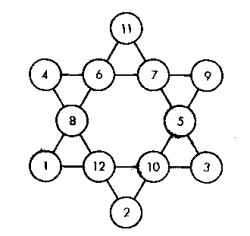
�No podr�a usted perfeccionar esta estrella, colocando los n�meros en los c�rculos de modo que no s�lo las filas tuvieran la misma cantidad (26), sino que esa misma cantidad (26) fuera la suma de los n�meros de las puntas?
Soluci�n
Para establecer con m�s facilidad la busca de la colocaci�n de los n�meros pedida, nos guiaremos por los siguientes c�lculos:
La suma buscada de los n�meros de las puntas de la estrella equivale a 26; la suma de todos los n�meros de la estrella es igual a 78. Es decir, que la suma de los n�meros del hex�gono interior equivale a 78 - 26 = 52.
La suma de los n�meros de cada lado es 26; si sumamos los tres lados obtendremos
sin olvidar que cada n�mero situado en un �ngulo se cuenta dos veces. Como la suma de los tres pares interiores (es decir, del hex�gono interior) debe ser, seg�n sabemos, igual a 52, resulta que la suma duplicada de los n�meros de los �ngulos de cada tri�ngulo equivale a
la suma sencilla ser�, pues, igual a 13.
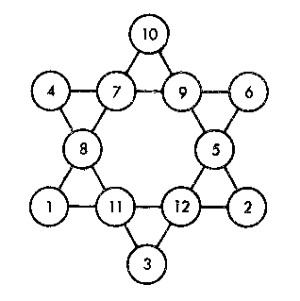
El n�mero de combinaciones queda as� considerablemente reducido. Por ejemplo, sabemos que ni el 12 ni el 11 pueden ocupar las puntas de la estrella (�por qu�?) . Esto quiere decir que podemos empezar a probar con el n�mero 10, con lo cual se determina enseguida qu� otros dos n�meros deben ocupar los restantes v�rtices del tri�ngulo: 1 y 2.
Siguiendo este camino, encontramos definitivamente la distribuci�n que nos piden. Es la indicada en la figura.
Volver