Cap�tulo 8
Rompecabezas de geometr�a

Contenido:
62. La carreta
63. La lente biconvexa
64. El nivel de la burbuja
65. N�mero de caras
66. El cuarto creciente de la Luna
67. Con 12 cerillas
68. Con ocho cerillas
69. �Qu� camino debe seguir la mosca?
70. Hacer pasar una moneda de cinco pesetas
71. Hallar la altura de una torre
72. Las figuras semejantes
73. La sombra del cable
74. El ladrillito
75. El gigante y el enano
76. Dos sand�as
77. Dos melones
78. La cereza
79. El modelo de la torre Eiffel
80. Dos cacerolas
81. �Qui�n tiene m�s fr�o?
82. El az�car

Para resolver los rompecabezas incluidos en este cap�tulo no se requiere haber estudiado un curso completo de geometr�a; basta sencillamente conocer las nociones m�s elementales de esta rama de la ciencia. Las dos docenas de problemas descritos en este cap�tulo ayudar�n al lector a darse cuenta de en qu� grado domina los conocimientos de geometr�a que consideraba asimilados. Conocer bien la geometr�a quiere decir no s�lo saber enumerar las propiedades de las figuras, sino tambi�n poder utilizar h�bilmente estas propiedades para resolver problemas reales.

62. La carreta
�Por qu� el eje delantero de una carreta se desgasta m�s y se calienta con mayor frecuencia que el trasero?

Soluci�n
A primera vista parece como si este problema no tuviera relaci�n alguna con la geometr�a. Pero en eso estriba precisamente el dominio de esta ciencia, en saber descubrir los principios geom�tricos en que est�n fundados los problemas, cuando se encuentran ocultos entre detalles accesorios. Nuestra tarea es, sin duda, puramente geom�trica. Sin poseer suficientes conocimientos de geometr�a, no es posible resolver ese problema.
As�, pues, �por qu� el eje delantero de la carreta se desgasta m�s r�pidamente que el trasero? De todos es conocido que el di�metro de las ruedas delanteras es menor que el de las traseras. En un mismo recorrido, el n�mero de vueltas que da la rueda peque�a es siempre mayor. En la peque�a, el per�metro, de la circunferencia exterior es menor, por lo cual cabe m�s veces en la longitud dada. Se comprende, por tanto, que en cualquier recorrido que haga la carreta, las ruedas delanteras dar�n m�s vueltas que las traseras, y naturalmente, a mayor n�mero de revoluciones, el desgaste del eje ser� m�s intenso
Volver

63. La lente biconvexa
Con una lupa, que aumenta cuatro veces, se observa un �ngulo de grado y medio. �Con qu� magnitud se ve?

Soluci�n


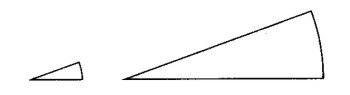
Se equivocan ustedes si piensan que a trav�s de la lupa, nuestro �ngulo resulta de una magnitud 1 1/2 x 4 = 6�. La magnitud del �ngulo no aumenta lo m�s m�nimo al mirarlo a trav�s de la lupa. Es verdad que el arco del �ngulo que se mide aumenta sin duda alguna, pero en la misma proporci�n aumentar� tambi�n el radio de dicho arco, de modo que la magnitud del �ngulo central quedar� invariable. La figura aclarar� lo dicho.
Volver

64. El nivel de la burbuja
Conocen ustedes, naturalmente, este tipo de nivel, con su burbuja de aire indicadora que se desplaza a la izquierda o a la derecha de la marca �ndice cuando se inclina la base del nivel respecto del horizonte. Cuanto mayor sea la inclinaci�n, tanto m�s se alejar� la burbuja de la marca central. La burbuja se mueve porque es m�s ligera que el l�quido que la contiene, y por ello asciende, tratando de ocupar el punto m�s elevado. Pero si el tubo fuera recto, la burbuja, al sufrir �l nivel la menor inclinaci�n, se desplazar�a a la parte extrema del tubo, o sea, a la parte m�s alta. Es f�cil comprender que un nivel de este tipo seria incomod�simo para trabajar. -Por tanto, el tubo del nivel se hace en forma curva. Cuando la base del nivel est� horizontal, la burbuja, al ocupar el punto m�s alto del tubo, se encuentra en su parte central. Si el nivel est� inclinado, el punto m�s elevado no coincidir� con la parte central del tubo, sino que se hallar� en otro punto pr�ximo a la marca, y la burbuja se desplazar� respecto de la marca �ndice, situ�ndose en otro lugar del tubo, que entonces ser� el m�s alto.
Se trata de determinar cu�ntos mil�metros se separa la burbuja de la marca si el nivel tiene una inclinaci�n de medio grado y el radio de curvatura del tubo es de 1 m.

Soluci�n


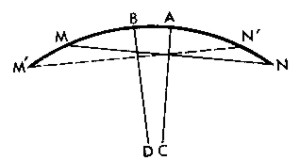
Examine la figura en la cual MAN indica la posici�n inicial del arco de nivel y M'BN la nueva posici�n. La cuerda M'N' forma con la cuerda MN un �ngulo de medio grado. La burbuja, que se hallaba antes en el punto A, no cambia de lugar, mientras que el punto central del arco MN pasa a ocupar la posici�n B. Se trata de calcular la longitud del arco AB, sabiendo que su radio es de 1 m y que el �ngulo correspondiente a dicho arco es de medio grado (esto se deduce de la igualdad de �ngulos agudos con lados perpendiculares).
El c�lculo no es dif�cil. La longitud de la circunferencia total, para un radio de 1 m (1.000 mm), es igual a 2 x 3,14 x 1.000 = 6.280 mm. Como la circunferencia tiene 360� o 720 medios grados, la longitud correspondiente a medio grado ser�
6.280: 720 = 8,7 mm.

La burbuja se desplazar� respecto de la marca (mejor dicho, la marca se desplazar� respecto de la burbuja) unos 9 mm, casi un cent�metro. L�gicamente se comprende que cuanto mayor sea el radio de curvatura del tubo, tanto mayor ser� la sensibilidad del nivel.
Volver

65. N�mero de caras
He aqu� una pregunta que sin duda alguna parecer� muy c�ndida, o por el contrario, demasiado sutil. �Cu�ntas caras tiene un l�piz de seis aristas?
Antes de mirar la respuesta, reflexione atentamente sobre el problema.

Soluci�n
Este problema se plantea en serio, y est� basado en los errores habituales que se cometen al hacer un uso impropio de las palabras. Un l�piz de seis aristas no tiene seis caras, como seguramente piensa la mayor�a. Si no est� afilado, tiene ocho caras: seis laterales y dos frontales m�s peque�as. Si tuviera realmente seis caras, el l�piz tendr�a otra forma completamente distinta, la de una barrita de secci�n rectangular.
La costumbre de considerar en un prisma s�lo las caras laterales olvid�ndose de las bases, est� muy extendida. Muchos dicen �prisma de tres caras, de cuatro caras�, etc�tera, mientras que en realidad deben llamarse: triangular o tri�drico, cuadrangular o tetra�drico, etc., seg�n sea la forma de la base. No existen prismas de tres caras, o sea, prismas con tres aristas.
As�, pues, el l�piz de que se trata en el problema, debe llamarse, si se habla correctamente, no de seis caras, sino hexagonal o hexa�drico.
Volver

66. El cuarto creciente de la Luna
Se trata de dividir la figura de un cuarto creciente de la Luna en seis partes, trazando solamente dos l�neas rectas.


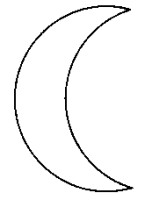
�C�mo hacerlo?
Soluci�n
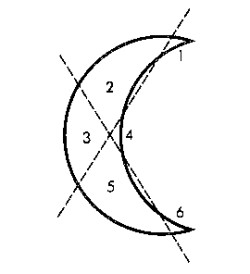
Debe efectuarse como se indica en la figura. Se obtienen seis partes, que numeramos para hacerlas m�s evidentes.

Volver

67. Con 12 cerillas
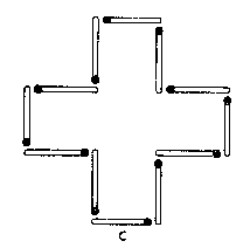
Con doce cerillas puede construirse la figura de una cruz (v�ase la figura), cuya �rea equivalga a la suma de las superficies de cinco cuadrados hechos tambi�n de cerillas.
Cambie usted la disposici�n de las cerillas de tal modo que el contorno de la figura obtenida abarque s�lo una superficie equivalente a cuatro de esos cuadrados.



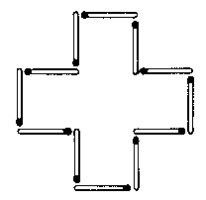
Para resolver este problema no deben utilizarse instrumentos de medici�n de ninguna clase.

Soluci�n




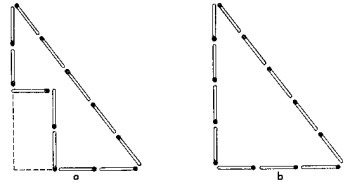
Las cerillas deben colocarse como muestra la figura a; la superficie de esta figura es igual al cu�druplo de la de un cuadrado hecho con cuatro cerillas. �C�mo se comprueba que esto es as�? Para ello aumentamos mentalmente nuestra figura hasta obtener un tri�ngulo. Resulta un tri�ngulo rect�ngulo de tres cerillas de base y cuatro de altura. Su superficie ser� igual a la mitad del producto de la base por la altura: 1/2 x 3 x 4 = 6 cuadrados de lado equivalente a una cerilla (v�ase figura b). Pero nuestra figura tiene evidentemente un �rea menor, en dos cuadrados, que la del tri�ngulo completo, y por lo tanto, ser� igual a cuatro cuadrados, que es lo que buscamos.

Volver

68. Con ocho cerillas
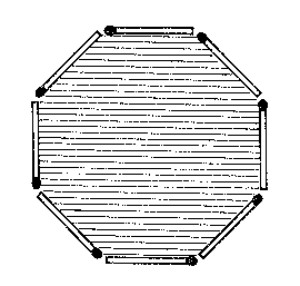
Con ocho cerillas pueden construirse numerosas figuras de contorno cerrado. Algunas pueden verse en la figura; su superficie es, naturalmente, distinta.



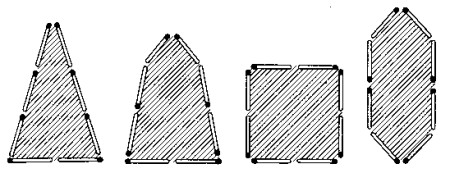
Se plantea c�mo construir con 8 cerillas la figura de superficie m�xima.

Soluci�n
Puede demostrarse que de todas las figuras con contornos de id�ntico per�metro, la que tiene mayor �rea es el c�rculo. Naturalmente que bas�ndose en cerillas no es posible construir un c�rculo; sin embargo, con ocho cerillas puede componerse la figura m�s aproximada al c�rculo, un oct�gono regular (v�ase la figura). El oct�gono regular es la figura que satisface las condiciones exigidas en nuestro problema, pues es la que, con igual n�mero de cerillas, posee mayor superficie.


Volver

69. �Qu� camino debe seguir la mosca?
En la pared interior de un vaso cil�ndrico de cristal hay una gota de miel situada a tres cent�metros del borde superior del recipiente. En la pared exterior, en el punto diametralmente opuesto, se ha parado una mosca.
Ind�quese cu�l es el camino m�s corto que puede seguir la mosca para llegar hasta la gota de miel.


La altura del vaso es de 20 cm y el di�metro de 10 cm.
No piensen ustedes que la mosca va a encontrar ella misma el camino m�s corto y facilitar as� la soluci�n del problema; para ello es necesario poseer ciertos conocimientos de geometr�a, demasiado vastos para el cerebro de una mosca.

Soluci�n
Para resolver este problema hay que desarrollar la superficie lateral del vaso cil�ndrico, extendi�ndola en un plano. En esta forma obtendremos un rect�ngulo (v�ase la figura) de 20 cm de altura y una base cuya longitud es igual a la circunferencia del vaso, o sea, 10 x 3 1/7 = 31 1/2 cm (aproximadamente). Marquemos en este rect�ngulo los lugares correspondientes a la mosca y a la gotita de miel. La mosca est� en el punto A, situado a 17 cm de la base; la gotita de miel, en el punto B, a la misma altura y distante del punto A la longitud correspondiente a media circunferencia del vaso, o sea, 15 3/4 CM.
Para hallar ahora el punto donde la mosca ha de cruzar el borde del vaso pasando a su interior, hay que hacer lo siguiente. Tracemos desde el punto B (v�ase la figura), dirigida hacia arriba, una perpendicular a AB y continu�ndola hasta el punto C equidistante del punto B con relaci�n al borde del vaso. Seguidamente, tracemos la recta CA. El punto de intersecci�n D ser� donde la mosca cruce el borde, al pasar al otro lado del vaso. El camino ADB ser� el m�s corto.
Una vez hallado el camino m�s corto en el rect�ngulo desplegado, lo enrollamos de nuevo en forma de cilindro y veremos perfectamente qu� ruta debe seguir la mosca para llegar con m�s rapidez hasta la gotita de miel (v�ase la figura).
No puedo asegurar que la mosca vaya a elegir en un caso semejante dicho camino. Es posible que orient�ndose por el olfato, la mosca efectivamente marche por la trayectoria m�s corta, pero no es muy probable, pues el olfato en estos casos no es un sentido que ofrezca tanta precisi�n.
Volver

70. Hacer pasar una moneda de cinco pesetas
Tomen dos monedas: una de cinco pesetas y otra de diez c�ntimos. Dibujen en una hoja de papel un c�rculo exactamente igual a la circunferencia de la moneda de diez c�ntimos y rec�rtenlo cuidadosamente.
�Podr� pasar la moneda de cinco pesetas por ese orificio?No se trata de un truco, es un verdadero problema geom�trico.

Soluci�n
Aunque parezca extra�o, la moneda de cinco pesetas puede pasar por un orificio tan peque�o. Para ello, se necesita solamente saber hacerlo. Se dobla la hoja de papel de manera que se alargue el orificio circular y adquiera la forma de una ranura (v�ase la figura). Por esa ranura pasa perfectamente la moneda de cinco pesetas.
El c�lculo geom�trico ayuda a comprender este truco, que a primera vista parece complicado. El di�metro de la moneda de diez c�ntimos es de 18 mm. Su circunferencia, f�cil de calcular, es de poco menos de 57 mm. La longitud de la ranura rectil�nea ser�, evidentemente, la mitad del per�metro, o sea, unos 28 mm. Por otra parte, el di�metro de la moneda de cinco pesetas es de 23 mm; por lo tanto, puede pasar sin dificultad por la ranura de 28 mm incluso teniendo en cuenta su espesor (1 1/2 mm).
Volver

71. Hallar la altura de una torre
En la ciudad donde usted vive hay, sin duda, algunos monumentos notables, y entre ellos una torre cuya altura seguramente desconoce. Dispone usted de una postal con la fotograf�a de la torre.�En qu� forma puede esta foto ayudarle a averiguar la altura de la torre?

Soluci�n
Para determinar por la fotograf�a la altura de la torre en su tama�o natural, hay que medir, lo m�s exactamente posible, la altura de la torre y la longitud de su base en la foto. Supongamos que obtenemos: para la altura 95 mm, y para la longitud de la base 19 mm. Despu�s se mide la longitud de la base de la torre directamente del natural. Supongamos que sea igual a 14 metros.
Hagamos ahora el razonamiento siguiente.
La torre y su imagen en la fotograf�a poseen configuraciones geom�tricas semejantes. Por consiguiente, la proporci�n entre las dimensiones de la base y la altura, en ambos casos, ser� la misma. En la foto es de 95 : 19 = 5; de donde deducimos que la altura de la torre es cinco veces mayor que su base, es decir, 14 x 5 = 70 metros.
Por lo tanto, la torre de la ciudad tiene 70 m de altura.
Sin embargo, hay que hacer notar que para determinar por el m�todo fotogr�fico la altura de la torre no sirve cualquier fotograf�a, sino s�lo las que no alteren las proporciones, cosa poco frecuente en fot�grafos con poca experiencia.
Volver

72. Las figuras semejantes
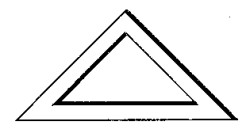
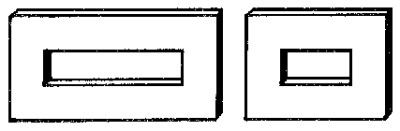
Este problema va destinado a los que sepan en qu� consiste la semejanza geom�trica. Se trata de responder a las dos preguntas siguientes: 1) En un cartab�n de dibujo (v�ase la figura), �son semejantes los tri�ngulos exterior e interior? 2) En un marco, �son semejantes los rect�ngulos exterior e interior?





Soluci�n
De ordinario, a las dos preguntas planteadas en este problema se contesta afirmativamente, lo que es un error. En realidad, son semejantes �nicamente los tri�ngulos; los rect�ngulos exterior e interior en general, no son semejantes. Para que los tri�ngulos sean semejantes es suficiente la igualdad de sus �ngulos, y, puesto que los lados de ambos tri�ngulos, interior y exterior, son paralelos, las dos figuras ser�n seme antes. Pero para que se cumpla la semejanza geom�trica en otros pol�gonos no basta con la igualdad de los �ngulos (o lo que es lo mismo, con el paralelismo de los lados); es necesario que los lados de ambos pol�gonos circunscritos sean, adem�s, proporcionales. En el marco, para los rect�ngulos exterior e interior, esto se verifica s�lo cuando son cuadrados (y en general, rombos). En todos los dem�s casos, los lados del rect�ngulo exterior no son proporcionales a los del interior, y por tanto, los rect�ngulos no son semejantes. La falta de semejanza se hace m�s notoria en los marcos anchos y de forma rectangular, como puede verse en la figura. En el marco de la izquierda, las longitudes de los lados del rect�ngulo exterior se hallan en la proporci�n de 2 : 1 y en el interior de 4 : 1. En el marco de la derecha, para los exteriores es de 4 : 3 y para los interiores de 2 : 1.
Volver

73. La sombra del cable
�A qu� distancia se extiende en el espacio la sombra total producida por un cable telegr�fico de 4 mm de di�metro?
Soluci�n
Es posible que a muchos les sorprenda que la soluci�n de este problema requiera ciertos conocimientos de astronom�a referentes a la distancia de la Tierra al Sol y a la magnitud del di�metro solar.


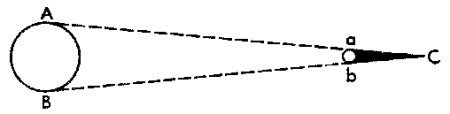
La longitud de la sombra total formada en el espacio por el alambre puede determinarse geom�tricamente por el esquema representado en la figura. Es f�cil ver que la sombra es mayor que el di�metro del alambre en la misma proporci�n que la distancia que separa el Sol de la Tierra (150.000.000 de km) lo es respecto del di�metro del Sol (1.400.000 km). La �ltima relaci�n es, en n�meros redondos, igual a 115. Esto significa que la longitud de la sombra total que forma el alambre en el espacio es:
4 x 115 = 460 mm = 46 cm.

La longitud insignificante de la sombra total proyectada explica el que la sombra no se vea con nitidez en la tierra o en los muros de las casas; las rayas d�biles que se distinguen en estos casos, no son sombras propiamente dichas, sino semisombras.
Al examinar el rompecabezas n�mero 7 hemos indicado otra forma de resolver problemas de este tipo.
Volver

74. El ladrillito
Un ladrillo, de los usados en la construcci�n, pesa unos cuatro kilogramos. �Cu�nto pesar� un ladrillito de juguete hecho del mismo material y cuyas dimensiones sean todas cuatro veces menores?

Soluci�n
La respuesta de que el ladrillito de juguete pesa 1 kg, o sea, la cuarta parte, es una gran equivocaci�n. El ladrillito no s�lo es cuatro veces m�s corto que el ladrillo de verdad, sino que tambi�n es cuatro veces m�s estrecho y m�s bajo; por lo tanto, su volumen y peso son 4 x 4 x 4 = 64 veces menores. La respuesta correcta es:
El ladrillito de juguete pesa 4.000: 64 = 62,5 gramos.
Volver

75. El gigante y el enano
�Cu�ntas veces es m�s pesado un gigante de 2 m de altura que un enano de 1 m?

Soluci�n
Est�n ustedes ya bastante preparados para resolver este problema. En virtud de que las figuras humanas son aproximadamente semejantes, al ser la estatura dos veces mayor, su volumen ser�, no el doble, sino ocho veces mayor. Esto quiere decir que nuestro gigante es ocho veces m�s pesado que el enano. El gigante m�s alto de que se tiene noticia fue un habitante de Alsacia de 275 cm de altura: o sea, un metro m�s alto que cualquier persona de estatura normal. El enano m�s peque�o conocido ten�a una altura menor de 40 cm, o sea, era unas siete veces m�s bajo que el tit�n alsaciano.
Por lo tanto, si en uno de los platillos de la balanza se coloca el gigante de Alsacia, en el otro ser� necesario, para conseguir el equilibrio, colocar 7 x 7 x 7 = 343 enanos, un verdadero tropel de gente.
Volver

76. Dos sand�as
Hay a la venta dos sand�as de tama�o diferente. Una de ellas es la cuarta parte m�s ancha que la otra y cuesta vez y media m�s cara. �Cu�l de las dos es m�s ventajoso comprar?

Soluci�n
El volumen de la sand�a mayor supera al de la menor casi el doble.
Por consiguiente, es m�s ventajoso comprar la sand�a mayor. Esta sand�a es vez y media m�s cara, pero, en cambio, la parte comestible es dos veces mayor.
Sin embargo, �por qu� los vendedores piden, de ordinario, por tales sand�as un precio no doble sino s�lo vez y media mayor? Se explica eso simplemente porque los vendedores, en la mayor�a de los casos, no est�n fuertes en geometr�a. Por otra parte, tampoco conocen bien esta materia los compradores, que a menudo, se niegan a comprar, por esta causa, mercanc�as ventajosas. Puede afirmarse que es m�s lucrativo comprar sand�as grandes que peque�as, puesto que aqu�llas se valoran siempre por debajo de su precio verdadero; no obstante, muchos de los compradores no se dan cuenta de ello.
Por esta misma raz�n, es siempre m�s ventajoso comprar huevos grandes que menudos si no se venden a peso.
Volver

77. Dos melones
Est�n a la venta dos melones de la misma calidad. Uno tiene 60 cent�metros de per�metro, el otro 50 cm. El primero cuesta vez y media m�s caro que el segundo; �Qu� mel�n es m�s ventajoso comprar?

Soluci�n
La relaci�n existente entre las longitudes de las circunferencias es igual a la de sus di�metros respectivos. Si la circunferencia de un mel�n mide 60 cm y la de otro 50 cm, la relaci�n entre sus di�metros ser� de 60 : 50 = 6/5, y la relaci�n entre los vol�menes ser�:
El mel�n mayor debe costar, si se valora con arreglo a su volumen (o peso), 1,73 veces m�s que el menor; en otras palabras, el 73 % m�s caro. En total, s�lo piden el 50 % m�s. Est� claro que tiene m�s cuenta comprar el mayor.
Volver

78. La cereza
La parte carnosa y el hueso de una cereza son de la misma anchura. Supongamos que la cereza y el hueso tengan forma esf�rica.
�Puede usted calcular cu�ntas veces es mayor el volumen de la parte jugosa que el del hueso?

Soluci�n
De las condiciones impuestas por el problema se deduce que el di�metro de la cereza es tres veces mayor que el di�metro del hueso, lo que significa que el volumen de la cereza es 3 x 3 x 3 = 27 veces mayor que el del hueso. Al hueso le corresponde 1/27 del volumen de la cereza, mientras que a la parte carnosa, lo restante, es decir, 26/27. Por consiguiente, el volumen de la parte carnosa de la cereza es 26 veces mayor que el del hueso.
Volver

79. El modelo de la torre Eiffel
La torre Eiffel de Par�s tiene 300 m de altura y est� construida enteramente de hierro; su peso total es de 8.000.000 de kilogramos.
Deseo encargar un modelo exacto de dicha torre, tambi�n de hierro, y que pese s�lo 1 kg. �Qu� altura tendr�? �Ser� mayor o menor que la de un vaso?

Soluci�n
Si el modelo pesa 8.000.000 de veces menos que la torre y ambos est�n hechos del mismo metal, el volumen del modelo debe ser 8.000.000 menor que el de la torre. Sabemos que la relaci�n entre los vol�menes de los cuerpos semejantes es igual a la que existe entre los cubos de sus alturas respectivas. Por consiguiente, el modelo debe ser 200 veces m�s bajo que el natural, puesto que
200 x 200 x 200 = 8.000.000

La altura de la torre es de 300 metros. De donde se deduce que la altura del modelo es

300 : 200 = 1 1/2 m.
Volver

80. Dos cacerolas
Tenemos dos cacerolas de cobre de igual forma con las paredes de id�ntico espesor. La capacidad de la primera es 8 veces mayor que la segunda. �Cu�ntas veces es m�s pesada la primera?

Soluci�n
Ambas cacerolas son dos cuerpos geom�tricamente semejantes. Si la cacerola grande tiene una capacidad ocho veces mayor, todas sus dimensiones lineales tendr�n el doble de longitud: ser� el doble de alta y el doble de ancha en ambas direcciones. Siendo el doble de alta y de ancha, su superficie ser� 2 x 2 = 4 veces mayor, puesto que la relaci�n entre las superficies de los cuerpos semejantes es id�ntica a la de los cuadrados de sus dimensiones lineales. Si las paredes tienen el mismo espesor, el peso de las cacerolas depende de las �reas de sus superficies respectivas. Lo expuesto nos da respuesta a la pregunta formulada en el problema: la cacerola grande es cuatro veces m�s pesada que la peque�a.
Volver

81. �Qui�n tiene m�s fr�o?
Un d�a de fr�o, una persona mayor y un ni�o est�n al aire libre.
Ambos van igualmente vestidos. �Cu�l de los dos tiene m�s fr�o?

Soluci�n
A primera vista, este problema parece como si no estuviera relacionado con las matem�ticas; sin embargo, en lo fundamental, se resuelve bas�ndose en razonamientos geom�tricos, de modo semejante a como se ha explicado el problema anterior.
Antes de proceder a su resoluci�n, examinemos un problema parecido, pero algo m�s sencillo.
Supongamos dos calderas, una grande y otra peque�a, de id�ntica forma y construidas del mismo metal. Ambas est�n llenas de agua hirviente. �Cu�l de ellas se enfriar� antes?
Los objetos irradian el calor a trav�s de su superficie; por tanto, se enfriar� m�s r�pidamente aquella caldera en que a cada unidad de volumen corresponda mayor superficie de irradiaci�n. Si una de las calderas es n veces m�s alta y ancha que la otra, la superficie de la primera ser� n2 veces mayor y su volumen n3 veces; a la caldera de mayor tama�o le corresponde, por cada unidad de superficie, un volumen n veces mayor. Por consiguiente, la caldera menor debe enfriarse antes.
Por la misma causa, la criatura expuesta al fr�o debe sentir �ste m�s que la persona adulta, si ambas est�n igualmente abrigados, puesto que la cantidad de calor que se origina en cada cm ³ del cuerpo, es en ambos casi id�ntica; sin embargo, la superficie del cuerpo que se enfr�a, correspondiente a un cm3, es mayor en la criatura que en la persona adulta.
As� se explica que se enfr�en con m�s intensidad los dedos de las manos y la nariz, y que se hielen con mayor frecuencia que otras partes del cuerpo, cuya superficie no es tan grande en comparaci�n con su volumen.
Para terminar, examinemos el problema siguiente: �Por qu� una astilla arde con mayor rapidez que el le�o del que se ha cortado?
Debido a que el calentamiento se verifica en la superficie y se difunde por todo el volumen del cuerpo, habr� que establecer la relaci�n existente entre la superficie y el volumen de la astilla (por ejemplo, de secci�n cuadrada) con la superficie y el volumen de un le�o de id�ntica longitud y secci�n, y de este modo, determinar cu�l ser� la superficie que corresponda a cada cm3 de madera en ambos casos. Si el grosor del le�o es diez veces mayor que el de la astilla, la superficie lateral del le�o ser� tambi�n diez veces mayor que la de la astilla, y el volumen del primero ser� cien veces mayor que el de la astilla. Por consiguiente, a cada unidad de superficie de la astilla, si la comparamos con el le�o, le corresponde la d�cima parte del volumen. La misma cantidad de calor act�a sobre ambos, pero en la astilla calienta un volumen de madera diez veces menor, lo que explica que la astilla se inflame con mayor rapidez que el le�o del que formaba parte.
Por ser la madera mala conductora del calor, las proporciones indicadas hay que considerarlas s�lo aproximadas; caracterizan �nicamente la marcha general del proceso y no el aspecto cuantitativo del mismo.
Volver

82. El az�car
�Qu� pesa m�s, un vaso lleno de az�car en polvo o de az�car en terrones?

Soluci�n
Si no hacemos un peque�o esfuerzo de imaginaci�n, este problema parecer� muy dif�cil; sin embargo, su soluci�n es muy sencilla. Supongamos, para mayor sencillez, que los terrones de az�car tengan una magnitud cien veces mayor que las part�culas de az�car en polvo. Imaginemos ahora que todas las part�culas de az�car en polvo aumenten de tama�o cien veces, junto con el vaso que las contiene. El vaso adquirir�a una capacidad 100 x 100 x I(X) = 1.000.000 de veces mayor. En esta misma proporci�n aumentar� el peso del az�car en �l contenido. Tomemos mentalmente un vaso corriente de este az�car en polvo (aumentado cien veces), o sea, una millon�sima del vaso gigante. La cantidad tomada pesar�, naturalmente, tanto como pesa un vaso ordinario de az�car en polvo corriente. �Qu� representa en s� este az�car en polvo que hemos tomado agrandado de tama�o? Al fin y al cabo, lo mismo que el az�car en terrones. Esto quiere decir que el vaso contiene, en peso, la misma cantidad de az�car en polvo que de az�car en terrones.
Si aument�ramos el tama�o de las part�culas de az�car, no cien veces, sino sesenta u otro cualquier n�mero de veces, el problema no cambiar�a en absoluto. El razonamiento est� basado en que los trozos de az�car en terrones pueden considerarse como cuerpos geom�tricamente semejantes a las part�culas de az�car en polvo y que est�n tambi�n distribuidos en el vaso en forma semejante.
Volver