Cap�tulo 2
La matem�tica en el domin� y el croquet

Contenido:
13. L�nea de 28 fichas
14. El comienzo y el final de la l�nea
15. Un truco con el domin�
16. El marco
17. Los siete cuadrados
18. Los cuadrados m�gicos del domin�
19. Progresi�n con las fichas del domin�
20. �Pasar bajo los aros o golpear la bola del contrario?
21. La bola y el poste
22. �Pasar el aro o chocar con el poste?
23. �Pasar la ratonera o dar en la bola del contrario?
24. La ratonera impracticable




13. L�nea de 28 fichas
�Por qu� las 28 fichas del domin� pueden colocarse, siguiendo las reglas del juego, formando una l�nea?

Soluci�n
A fin de simplificar el problema, dejemos por ahora a un lado los 7 dobles: 0 - 0, 1 - 1, 2 - 2, 3 - 3, 4 - 4, 5 - 5, 6 - 6. Nos quedan 21 fichas en las que cada n�mero de tantos se repite seis veces. Por ejemplo, tenemos que todos los cuatro ser�n:
4 - 0; 4 - 1; 4 - 2; 4 - 3; 4 - 4; 4 - 5; 4 - 6.
As�, pues, cada n�mero de tantos se repite un n�mero par de veces, con lo cual las fichas que forman cada grupo pueden casarse una con otra hasta que se agote el grupo. Una vez hecho eso, cuando nuestras 21 fichas est�n casadas formando una fila ininterrumpida, colocamos los siete dobles 0 - 0, 1 - 1, 2 - 2, etc., en los sitios correspondientes entre las dos fichas casadas. Entonces, las 28 fichas resultan, formando una sola l�nea, casadas seg�n las reglas del juego.
Volver

14. El comienzo y el final de la l�nea
Estando las 28 fichas casadas, en uno de los extremos hay 5 tantos. �Cu�ntos habr� en el otro extremo?

Soluci�n
Es f�cil demostrar que en la fila del domin� debe ser id�ntico el n�mero de tantos del final y del comienzo. En realidad, de no ser as�, el n�mero de tantos de los extremos de la fila se repetir�a un n�mero impar de veces (en el interior de la l�nea el n�mero de tantos est� formando parejas); sabemos, sin embargo, que en las fichas del domin�, cada n�mero de tantos se repite ocho veces: es decir, un n�mero par de veces. Por consiguiente, la suposici�n que el n�mero de tantos en los extremos de la l�nea no fuera el mismo, no es justa; el n�mero de tantos debe ser el mismo. (Razonamientos semejantes a �ste reciben en matem�tica la denominaci�n de demostraci�n por el contrario.)
De esta propiedad que acabamos de demostrar, se deduce que la l�nea de 28 fichas del domin� puede siempre cerrarse por los extremos formando un anillo. De aqu� que todas las fichas del domin� puedan casarse siguiendo las reglas del juego, y formar no s�lo una fila, sino un c�rculo cerrado.
Es posible que interese a los lectores saber cu�ntas l�neas o c�rculos diferentes de ese tipo pueden formarse. Sin entrar en detalles fatigosos de c�lculos, diremos que el n�mero de modos diferentes de distribuci�n que pueden formar las 28 fichas en una l�nea (o en un c�rculo) es enorme: pasa de 7 billones. Su n�mero exacto es:
7.959.229.931.520.
(Es el producto de los siguientes factores: 2 ¹³ x 3 ⁸ x 5 x 7 x 4.231).
Volver

15. Un truco con el domin�
Una persona toma una de las fichas y les propone que casen las 27 restantes, afirmando que es siempre posible hacerlo, cualquiera que sea la ficha tomada. Pasa a la habitaci�n contigua, para no ver c�mo lo hacen.
Empiezan ustedes a colocarlas y llegan a la conclusi�n de que dicha persona ten�a raz�n: las 27 fichas quedan casadas. Pero lo m�s asombroso es que, desde la otra habitaci�n y sin ver el domin�, tambi�n puede anunciar cu�ntos tantos hay en cada extremo de la fila de fichas.
�C�mo puede saberlo? �Por qu� est� seguro de que 27 fichas cualesquiera pueden colocarse en una sola l�nea cas�ndolas correctamente?

Soluci�n
La soluci�n de este rompecabezas se deduce de lo que acabamos de decir. Sabemos que las 28 fichas del domin� pueden casarse formando un c�rculo cerrado; por consiguiente, si de este c�rculo quitamos una ficha resultar� que:

1. Las otras 27 forman una fila ininterrumpida con los extremos sin casar;
2. Los tantos de los extremos de esta l�nea coincidir�n con los n�meros de la ficha que se ha quitado.

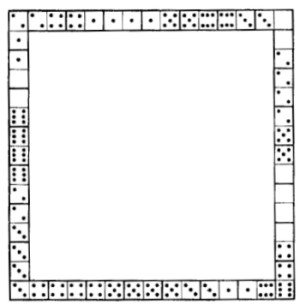
Escondiendo una ficha del domin�, podemos decir previamente el n�mero de tantos que habr� en los extremos de la l�nea por las otras fichas.
Volver

16. El marco
La figura reproduce un marco cuadrado, formado por las fichas del domin� de acuerdo con las reglas del juego.
Los lados del marco tienen la misma longitud, pero no igual n�mero de tantos; los lados superior e izquierdo contienen 44 tantos cada uno; de los otros dos lados, uno tiene 59 y el otro 32.
�Puede construirse un marco cuadrado cuyos lados contengan el mismo n�mero de tantos, es decir, 44 cada uno?

Soluci�n

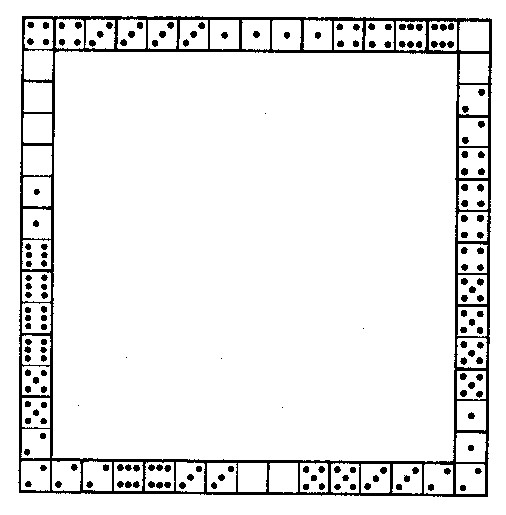
La suma de tantos del cuadrado buscado debe ser 44 x 4 = 176; es decir, 8 m�s que la suma de todos los tantos del domin� (168).
Esto ocurre porque el n�mero de tantos de las fichas que ocupan los �ngulos del cuadrado se cuentan dos veces. De lo dicho se deduce que la suma de los tantos en los extremos del cuadrado debe ser ocho. Esto facilita en cierto modo la colocaci�n exigida, aunque el encontrarla es bastante enredoso. La soluci�n viene indicada en la figura que se muestra a continuaci�n.
Volver

17. Los siete cuadrados
Cuatro fichas de domin�, elegidas convenientemente, pueden colocarse formando un cuadrado con id�ntico n�mero de tantos en cada lado. En la figura pueden ustedes ver un modelo donde la suma de los tantos de cada lado del cuadrado equivale siempre a 11.


�Podr�an ustedes formar con todas las fichas del domin� siete cuadrados de este tipo? No es necesario que la suma de tantos de cada lado de todos los cuadrados sea la misma. Lo que se exige es que los cuatro lados de cada cuadrado tengan id�ntico n�mero de tantos.

Soluci�n
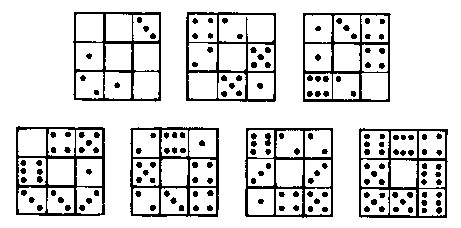
Damos dos soluciones de este problema entre las muchas posibles. En la primera (v�ase la figura) tenemos:

1 cuadrado con una suma de 3 1 cuadrado con una suma de 6 1 cuadrado con una suma de 8

1 cuadrado con una suma de 9 1 cuadrado con una suma de 10 1 cuadrado con una suma de 16

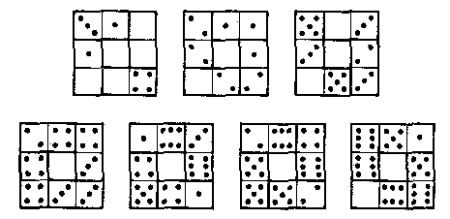
En la segunda soluci�n (v�ase figura) tenemos

2 cuadrado con una suma de 4 1 cuadrado con una suma de 8

2 cuadrado con una suma de 10 2 cuadrado con una suma de 12

Volver

18. Los cuadrados m�gicos del domin�
La figura muestra un cuadrado formado por 18 fichas de domin�, y que ofrece el inter�s de que la suma de los tantos de cualquiera de sus filas - longitudinales, transversales y diagonales - es en todos los casos igual a 13. Desde antiguo, estos cuadrados se llaman m�gicos .


Trate de construir algunos cuadrados m�gicos compuestos de 18 fichas, pero en los que la suma de tantos sea otra diferente. Trece es la suma menor en las filas de un cuadrado m�gico formado de 18 fichas. La suma mayor es 23.

Soluci�n
La figura contigua ofrece un modelo de cuadro m�gico con 18 tantos en cada fila:



Volver

19. Progresi�n con las fichas del domin�
En la figura se ven seis fichas de domin� casadas seg�n las reglas del juego, con la particularidad de que la suma total de tantos de cada ficha (en ambas mitades de cada una) aumenta


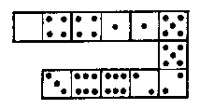
sucesivamente en una unidad: empezando con la suma 4, la serie consta de los siguientes n�meros de puntos:
4, 5, 6, 7, 8, 9.
La serie de n�meros en que cada t�rmino consecutivo aumenta (o disminuye) en la misma cantidad respecto del anterior se llama progresi�n aritm�tica. En la serie que acabamos de exponer, cada t�rmino es mayor que el precedente en una unidad, pero la diferencia entre los t�rminos de una progresi�n puede tener otro valor.
Se trata de formar progresiones a base de 6 fichas.

Soluci�n
En total se pueden formar 23 progresiones a base de las 6 fichas. Las fichas iniciales son las siguientes:
a) para progresiones en las que la raz�n es 1:

0-0 0-1 1-0 0-2

1-1 2-0 0-3 1-2

2-1 3-0 0-4 1-3

2-2 3-1 1-4 2-3

3-2 2-4 3-5 3-4

b) para progresiones en las que la raz�n es 2:

0-0

0-2

0-1

Volver

20. �Pasar bajo los aros o golpear la bola del contrario?
Los aros del croquet tienen forma rectangular. Su anchura es dos veces mayor que el di�metro de las bolas. En estas condiciones, �qu� es m�s f�cil? �Pasar el aro sin rozar el alambre, desde la posici�n mejor, o a la misma distancia golpear la bola del contrario?

Soluci�n
Incluso un jugador h�bil dir� seguramente que, en las condiciones dadas, es m�s f�cil atravesar los aros que golpear la bola del contrario, puesto que los aros son dos veces m�s anchos que la bola. Sin embargo, esa idea es equivocada: los aros, cierto, son m�s anchos que la bola, pero el espacio libre para que la bola pase por el interior del aro es dos veces menor que el que la bola misma presenta al hacer blanco.


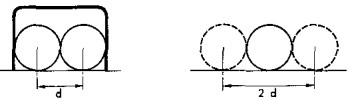
Observen la figura, y ver�n con claridad lo que acabamos de decir. El centro de la bola no debe acercarse al alambre del aro a una distancia inferior a su radio; en caso contrario, la bola tocar� el aro. Quiere decirse que al centro de la bola le queda un blanco que es dos radios menor que la anchura del aro. Puede verse con facilidad que en las condiciones dadas en nuestro problema, la anchura del blanco al atravesar el aro desde la posici�n m�s ventajosa, es igual a la magnitud del di�metro de la bola.
Veamos ahora la anchura del blanco en relaci�n con el centro de una bola en movimiento que golpea la del contrario. Es evidente que si el centro de la bola lanzada se aproxima al centro de la bola que debe ser golpeada a una distancia menor que un radio, el choque se realizar�. Esto quiere decir que la anchura del blanco en este caso, como puede verse en la figura, equivale a dos di�metros de la bola.
As�, pues, a pesar de lo que opinen los jugadores, en las condiciones expuestas, es dos veces m�s f�cil dar en la bola que pasar libremente el aro desde la mejor posici�n.
Volver

21. La bola y el poste
El poste de croquet, en su parte inferior, tiene un grosor de 6 cent�metros. El di�metro de la bola es de 10 cm. �Cu�ntas veces es m�s f�cil dar en la bola que, desde la misma distancia, pegar en el poste?

Soluci�n


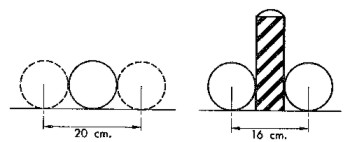
Despu�s de lo que acabamos de decir, el problema no exige detalladas explicaciones.
Puede verse f�cilmente (v�ase la figura de la p�gina siguiente) que la anchura del blanco en el caso de que la bola sea tocada, equivale a dos di�metros de la bola, o sea a 20 cm; mientras que la anchura del blanco al apuntar al poste es igual a la suma del di�metro de la bola y del poste, o sea, a 16 cm (v�ase la figura). De aqu� que acertar en la bola del contrario es
20 / 16 = 1 1/4 veces
o sea 25 % m�s f�cil que tocar el poste. Los jugadores de ordinario, aumentan mucho las probabilidades de tocar la bola al compararlas con las de dar en el poste.
Volver

22. �Pasar el aro o chocar con el poste?
La bola es dos veces m�s estrecha que los aros rectangulares y dos veces m�s ancha que el poste. �Qu� es m�s f�cil, pasar los aros sin tocarlos desde la posici�n mejor, o desde la misma distancia, pegar en el poste?

Soluci�n


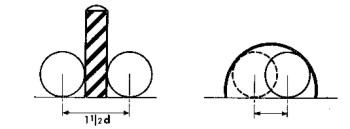
Cualquier jugador discurrir� del modo siguiente: Ya que el aro es doble de ancho que la bola, y el poste dos veces m�s estrecho que esta bola, el blanco ser� cuatro veces mayor para atravesar el aro que para dar en el poste. El lector aleccionado ya por los problemas anteriores, no incurrir� en semejante error. Calcular� que al apuntar al poste, el blanco es vez y media m�s ancho que para pasar a trav�s del aro desde la posici�n m�s ventajosa. Esto se ve claro en las figuras.
(Si los aros no fueran rectangulares, sino semicirculares, la probabilidad de paso de la bola ser�a a�n menor, como es f�cil deducirlo observando la figura.)
Volver

23. �Pasar la ratonera o dar en la bola del contrario?
La anchura de los aros rectangulares es tres veces mayor que el di�metro de la bola. �Qu� es m�s f�cil, pasar, desde la mejor posici�n, la ratonera sin tocarla, o desde la misma distancia, tocar la bola del contrario?

Soluci�n


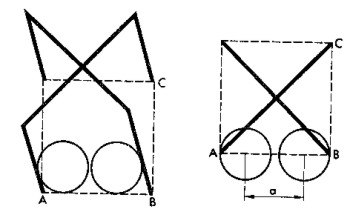
En las figuras se ve que el espacio a, que queda para el paso del centro de la bola, es bastante estrecho en las condiciones indicadas en el problema. Los que conocen la geometr�a saben que el lado AB del cuadrado es 1,4 veces menor que su diagonal AC. Si la anchura de los arcos es de 3d (siendo d el di�metro de la bola), AB ser� igual a:

El espacio a, blanco del centro de la bola que pasa la ratonera desde la posici�n m�s favorable, es todav�a m�s estrecho. Es un di�metro m�s peque�o e igual a:
2,1 d - d = 1,1 d.
Sin embargo, sabemos que el blanco referido al centro de la bola que va a tocar la del contrario equivale a 2d. Por consiguiente, es casi dos veces m�s f�cil tocar la bola del contrario, en las condiciones indicadas, que pasar la ratonera.
Volver

24. La ratonera impracticable
�Qu� relaci�n debe existir entre la anchura de los aros rectangulares y el di�metro de la bola, para que sea imposible atravesar la ratonera?

Soluci�n
Es imposible pasar la ratonera cuando la anchura del aro sobrepasa el di�metro de la bola menos de 1,4 veces. As� se deduce de las explicaciones dadas en el problema anterior. Si los aros tienen forma de arco circular, las condiciones del paso se complican todav�a m�s.
Volver