C O N T E N I D O
Pr�logo
1. Desayuno y rompecabezas
2. La matem�tica en el domin� y el croquet
3. Once rompecabezas m�s
4. �Sabe Usted Contar?
5. Rompecabezas num�ricos
6. Relatos de n�meros gigantes
7. Mediciones sin utilizar instrumentos
8. Rompecabezas de geometr�a
9. La geometr�a de la lluvia la nieve
10. Treinta problemas diferentes
Bajar parte 2
Escribir @ Antonio

Cap�tulo 1
Desayuno y rompecabezas
Contenido:
1. La ardilla en el calvero
2. Funcionamiento de los c�rculos escolares
3. �Qui�n cuenta m�s?
4. Los billetes de autocar
5. El vuelo del dirigible
6. La sombra
7. Un problema con cerillas
8. El toc�n traicionero
9. Un truco aritm�tico
10. La cifra tachada
11. Adivinar un n�mero sin preguntar nada
12. �Qui�n ha cogido cada objeto?
1. La ardilla en el calvero
- Hoy por la ma�ana he jugado al escondite con una ardilla - contaba a la hora del desayuno uno de los comensales en el albergue donde pas�bamos las vacaciones -. �Recuerdan ustedes el calvero circular del bosque con un abedul solitario en el centro'? Para ocultarse de m�, una ardilla se hab�a escondido tras ese �rbol. Al salir del bosque al claro, inmediatamente he visto el hociquito de la ardilla y sus vivaces ojuelos que me miraban fijamente detr�s del tronco. Con precauci�n, sin acercarme, he empezado a dar la vuelta por el contorno del calvero, tratando de ver al animalillo. Cuatro vueltas he dado alrededor del �rbol, pero la bribona se iba retirando tras del tronco en sentido contrario, sin ense�arme m�s que el hociquillo. En fin, no me ha sido posible dar la vuelta alrededor de la ardilla.
- Sin embargo - objet� alguien -, usted mismo ha dicho que dio cuatro veces la vuelta alrededor del �rbol.
- Alrededor del �rbol, s�; pero no alrededor de la ardilla. Pero la ardilla, �no estaba en el �rbol? - �Y qu�?
- Entonces usted daba tambi�n vueltas alrededor de la ardilla.
- �C�mo, si ni siquiera una vez le pude ver el lomo?
- �Pero qu� tiene que ver el lomo? La ardilla se halla en el centro, usted marcha describiendo un c�rculo, por lo tanto anda alrededor de la ardilla.
- Ni mucho menos. Imag�nese que ando junto a usted describiendo un c�rculo, y que usted va volvi�ndome continuamente la cara y escondiendo la espalda. �Dir�a usted que doy vueltas a su alrededor?
- Claro que s�. �Qu� hace usted si no?
- �Le rodeo, aunque no me encuentre nunca detr�s de usted, y no vea su espalda?
- �La ha tomado usted con mi espalda! Cierra el c�rculo usted a mi alrededor; ah� es donde est� el intr�ngulis, y no en que me vea o no la espalda.
- �Perdone! �Qu� significa dar vueltas alrededor de algo? - A mi entender no quiere decir nada m�s que lo siguiente: ocupar sucesivamente distintas posiciones de modo que pueda observarse el objeto desde todos los lados. �No es as�, profesor? - pregunt� uno de los interlocutores a un viejecillo sentado en la mesa.
- En realidad, est�n ustedes discutiendo sobre palabras - contest� el hombre de ciencia -. En estos casos hay que empezar siempre por lo que acaban de hacer; o sea, hay que ponerse de acuerdo en el significado de los t�rminos. �C�mo deben comprenderse las palabras "moverse alrededor de un objeto"? Pueden tener un doble significado. En primer lugar, pueden interpretarse como un movimiento por una l�nea cerrada en cuyo interior se halla el objeto. Esta es una interpretaci�n. Otra: moverse respecto a un objeto de modo que se le vea por todos los lados. Si aceptamos la primera interpretaci�n, debe reconocer que ha dado usted cuatro vueltas alrededor de la ardilla. Manteniendo la segunda, llegamos a la conclusi�n de que no ha dado vueltas a su alrededor ni una sola vez.
Como ven ustedes, no hay motivo para discutir, si ambas partes hablan en un mismo lenguaje y comprenden los t�rminos de la misma manera.
- Eso est� muy bien; puede admitirse una interpretaci�n doble. Pero, �cu�l es la justa?
- La cuesti�n no debe plantearse as�. Puede convenirse lo que se quiera. S�lo hay que preguntarse cu�l es la interpretaci�n m�s corriente. Yo dir�a que la primera interpretaci�n es la m�s acorde con el esp�ritu de la lengua, y he aqu� por qu�. Es sabido que el Sol da una vuelta completa alrededor de su eje en 26 d�as...
- �El Sol da vueltas?
- Naturalmente, lo mismo que la Tierra alrededor de su eje. Imaginen ustedes que la rotaci�n del Sol se realizara m�s despacio; es decir, que diera una vuelta no en 26 d�as, sino en 365 d�as y 1/4; o sea, en un a�o. Entonces el Sol tendr�a siempre el mismo lado orientado a la Tierra y nunca ver�amos la parte contraria, la espalda del Sol. Pero, �podr�a entonces afirmarse que la Tierra no daba vueltas alrededor del Sol?
- As�, pues, est� claro que a pesar de todo yo he dado vueltas alrededor de la ardilla.
- �Se�ores, no se vayan! - dijo uno de los que hab�an escuchado la discusi�n -. Quiero proponer lo siguiente. Como nadie va a ir de paseo, lloviendo como est�, y por lo visto la lluvia no va a cesar pronto, vamos a quedamos aqu� resolviendo rompecabezas. En realidad, ya hemos empezado. Que cada uno discurra o recuerde alg�n rompecabezas. Usted, profesor, ser� nuestro �rbitro.
- Si los rompecabezas son de �lgebra o de geometr�a, yo no puedo aceptar - declar� una joven.
- Ni yo tampoco - a�adi� alguien m�s.
- No, no; deben participar todos. Rogamos a los presentes que no hagan uso ni del �lgebra ni de la geometr�a; en todo caso, s�lo de los rudimentos. �Hay alguna objeci�n?
- Ninguna - dijeron todos -. �Venga, vamos a empezar!
Volver
2. Funcionamiento de los c�rculos escolares
- En nuestro Instituto - comenz� un estudiante de bachillerato - funcionan cinco c�rculos: de deportes, de literatura, de fotograf�a, de ajedrez y de canto. El de deportes funciona un d�a s� y otro no; el de literatura, una vez cada tres d�as, el de fotograf�a, una cada cuatro; el de ajedrez, una cada cinco, y el de canto, una cada seis. El primero e enero se reunieron en la escuela todos los c�rculos, y luego siguieron haci�ndolo en los d�as designados, sin perder ninguno. Se trata de adivinar cu�ntas tardes m�s, en el primer trimestre, se reunieron los cinco c�rculos a la vez.
- �El a�o era corriente o bisiesto? - preguntaron al estudiante.
- Corriente.
- �Es decir, que el primer trimestre, enero, febrero y marzo, fue de 90 d�as?
- Claro que s�.
- Perm�teme a�adir una pregunta m�s a la hecha por ti en el planteamiento del rompecabezas - dijo el profesor -. Es la siguiente: �cu�ntas tardes de ese mismo trimestre no se celebr� en el Instituto ninguna reuni�n de c�rculo?
- �Ah, ya comprendo! - exclam� alguien -. Es un problema con segundas... Me parece que despu�s del primero de enero, no habr� ni un d�a en que se re�nan todos los c�rculos a la vez, ni tampoco habr� uno en que no se re�na ninguno de los cinco. �Claro!
- �Por qu�?
- No puedo explicarlo, pero creo que quieren pescarle a uno. �Se�ores! - tom� la palabra el que hab�a propuesto el juego y al que todos consideraban como presidente de la reuni�n -. No hay que hacer p�blicas ahora las soluciones definitivas de los rompecabezas. Que cada uno discurra. El �rbitro, despu�s de cenar, nos dar� a conocer las contestaciones acertadas. �Venga el siguiente!
Soluci�n
Contestaremos f�cilmente a la primera cuesti�n -al cabo de cu�ntos d�as se reunir�n en la escuela a la vez los cinco c�rculos-, si sabemos encontrar el menor de todos los n�meros que se divida exactamente (m�nimo com�n m�ltiplo) por 2,3,4,5 y 6. Es f�cil comprender que este n�mero es el 60. Es decir, el d�a 61 se reunir�n de nuevo los 5 c�rculos: el de deportes, despu�s de 30 intervalos de dos d�as; el de literatura, a los 20 intervalos de 3 d�as; el de fotograf�a, a los 15 intervalos de cuatro d�as; el de ajedrez, a los 12 de 5 d�as, y el de canto, a los 10 de 6 d�as. Antes de 60 d�as no habr� una tarde as�. Pasados otros 60 d�as vendr� una nueva tarde semejante, durante el segundo trimestre.
As� pues, en el primer trimestre hay una sola tarde en la que se reunir�n de nuevo los cinco c�rculos a la vez. Hallar respuesta a la pregunta �cu�ntas tardes no se reunir� ning�n c�rculo? Resulta m�s complicado. Para encontrar esos d�as hay que escribir por orden los n�meros del 1 al 90 y tachar, en la serie, los d�as de funcionamiento del c�rculo de deportes; es decir, los n�meros 1, 3, 5, 7, 9, etc. Luego hay que tachar los d�as de funcionamiento del c�rculo de literatura: el 4, 10, etc. Despu�s de haber tachado los correspondientes a los c�rculos de fotograf�a, de ajedrez y de canto, nos quedar�n los d�as en que en el primer trimestre no haya funcionado ni un solo c�rculo.
Quien haga esta operaci�n se convencer� de que durante el primer trimestre son 24 los d�as en que no funciona ning�n c�rculo; 8 en enero: los d�as 2, 8, 12, 14, 18, 20, 24 y 30. En febrero hay 7 d�as as�, y en marzo, 9.
Volver
3. �Qui�n cuenta m�s?
Dos personas estuvieron contando, durante una hora, todos los transe�ntes que pasaban por la acera. Una estaba parada junto a la puerta, mientras la otra andaba y desandaba la acera. �Qui�n cont� m�s transe�ntes?
- Naturalmente, andando se cuentan m�s; la cosa est� clara - oy�se en el otro extremo de la mesa.
- Despu�s de cenar sabremos la respuesta - declar� el presidente -. �El siguiente!
Soluci�n
Ambos contaron el mismo n�mero de transe�ntes. El que estaba parado junto a la puerta contaba los transe�ntes que marchaban en ambas direcciones, mientras que el que andaba ve�a dos veces m�s personas que se cruzaban con �l.
Volver
4. Los billetes de autocar
- Soy taquillero en una estaci�n de autocares y despacho billetes - empez� a decir el siguiente participante en el juego -. A muchos esto les parecer� sencillo. No sospechan el n�mero tan grande de billetes que debe manejar el taquillero de una estaci�n, incluso de poca importancia. Es indispensable que los pasajeros puedan adquirir billetes de la indicada estaci�n a cualquier otra del mismo autocar. Presto mis servicios en una l�nea que consta de 25 estaciones. �Cu�ntos billetes distintos piensan ustedes que ha preparado la empresa para abastecer las cajas de todas las estaciones?
- Ha llegado su turno, se�or aviador - proclam� el presidente.
Soluci�n
En cada una de las 25 estaciones, los pasajeros pueden pedir billete para cualquier estaci�n, es decir, para los 24 puntos diferentes. Esto indica que el n�mero de billetes diferentes que hay que preparar es de 25 x 24 = 600.
Volver
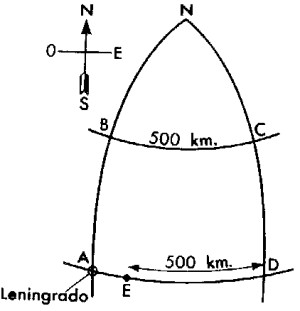
5. El vuelo del dirigible
- Imaginemos que despeg� de Leningrado un dirigible rumbo al norte. Una vez recorridos 500 km en esa direcci�n cambi� de rumbo y puso proa al este. Despu�s de volar en esa direcci�n 500 km, hizo un viraje de 900 y recorri� en direcci�n sur 500 km. Luego vir� hacia el oeste, y despu�s de cubrir una distancia de 500 km, aterriz�. Si tomamos como punto de referencia Leningrado, se pregunta cu�l ser� la situaci�n del lugar de aterrizaje del dirigible: al oeste, al este, al norte o al sur de esta ciudad.
- Este es un problema para gente ingenua - dijo uno de los presentes -. Siguiendo 500 pasos hacia delante, 500 a la derecha, 500 hacia atr�s y 500 hacia la izquierda, �ad�nde vamos a parar? Llegamos naturalmente al mismo lugar de donde hab�amos partido.
- �D�nde le parece, pues, que aterriz� el dirigible? - En el mismo aer�dromo de Leningrado, de donde hab�a despegado. �No es as�?
- Claro que no.
- �Entonces no comprendo nada!
- Aqu� hay gato encerrado - intervino en la conversaci�n el vecino -. �Acaso el dirigible no aterriz� en Leningrado ... ? �Puede repetir el problema?
El aviador accedi� de buena gana. Le escucharon con atenci�n, mir�ndose perplejos.
- Bueno - declar� el presidente -. Hasta la hora de la cena disponemos de tiempo para pensar en este problema. Ahora vamos a continuar.
Soluci�n
Este problema no contiene contradicci�n alguna. No hay que pensar que el dirigible vuela siguiendo el per�metro de un cuadrado; es necesario tener en cuenta la forma esferoidal de la Tierra. Los meridianos, al avanzar hacia el norte, se van aproximando (v�ase la figura); por ello, cuando vuela los 500 kil�metros siguiendo el arco del paralelo situado a 500 km al norte de la latitud de Leningrado, el dirigible se desplaza hacia oriente un n�mero de grados mayor que el que recorre despu�s en direcci�n contraria, al encontrarse de nuevo en la latitud de Leningrado. Como resultado de ello, el dirigible, al terminar el vuelo, estaba al este de Leningrado.
|
�Cu�nto? Esto puede calcularse. En la figura, ven ustedes la ruta seguida por el dirigible:ABCDE. El punto N es el Polo Norte; en ese punto se juntan los meridianos AB y CD. El dirigible vol� primero 500 km hacia el norte, es decir, siguiendo el meridiano AN.
Como la longitud de un grado de meridiano equivale a 111 km, el arco de meridiano de 500 km contendr� 500: 111 = 4 grados y medio. Leningrado est� situado en el paralelo 60; por consiguiente, el punto B se encuentra en los 60� + 4,5� = 64,5�. Despu�s, el dirigible vol� con rumbo este, es decir, por el paralelo BC, y recorri� sigui�ndolo, 500 km. La longitud de un grado en este paralelo puede calcularse (o verse en las tablas); equivale a 48 km. Es f�cil determinar cu�ntos grados recorri� el dirigible en direcci�n este, 500 : 48 = 10,4�. Luego, la nave a�rea tom� direcci�n sur, es decir, vol� siguiendo el meridiano CD y recorridos 500 km hab�a de encontrarse de nuevo en el paralelo de Leningrado. Ahora la ruta toma direcci�n oeste, es decir, va por AD; 500 km de este camino es evidentemente una distancia m�s corta que AD. En la distancia AD hay los mismos grados que en la BC, es decir, 10,40. Pero la distancia de un grado, a los 60� de latitud, equivale a 55,5 km. Por consiguiente, entre A y D existe una distancia igual a 55,5 x 10,4 = 577 km.
Vemos, pues, que el dirigible no pod�a aterrizar en Leningrado: le faltaron 77 km para llegar a este punto; es decir, que descendi� en el lago Ladoga.
Volver
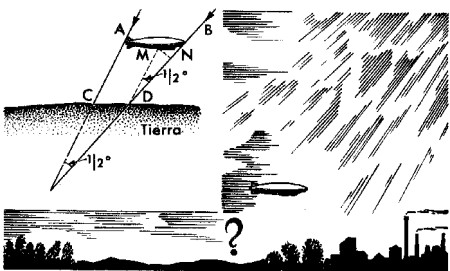
6. La sombra
- Perm�tanme tomar como tema de mi rompecabezas el mismo dirigible - dijo el participante de turno -. �Qu� es m�s largo, el dirigible o la sombra completa que proyecta sobre la Tierra?
- �Es �se todo el rompecabezas? - S�.
- La sombra, claro est�, es m�s larga que el dirigible; los rayos del Sol se difunden en forma de abanico - propuso inmediatamente alguien como soluci�n.
- Yo dir�a que, por el contrario, los rayos del Sol van paralelos - protest� alguien -. La sombra y el dirigible tienen la misma longitud.
- �Qu� va! �Acaso no ha visto usted los rayos divergentes del Sol oculto por una nube? De ello puede uno convencerse observando cu�nto divergen los rayos solares. La sombra del dirigible debe ser considerablemente mayor que el dirigible, en la misma forma que la sombra de la nube es mayor que la nube misma.
- �Por qu� se acepta corrientemente que los rayos del Sol son paralelos? Todos lo consideran as�...
El presidente no permiti� que la discusi�n se prolongara y concedi� la palabra al siguiente.
Soluci�n
Los que han hablado sobre este problema han cometido algunas faltas. No es cierto que los rayos del Sol que caen sobre la Tierra diverjan sensiblemente.
|
Comparada con la distancia que la separa del Sol, la Tierra es tan peque�a que los rayos del Sol que caen sobre cualquier parte de su superficie divergen en un �ngulo peque��simo, inapreciable; pr�cticamente pueden considerarse paralelos. A veces contemplamos, en la llamada irradiaci�n tras las nubes, que los rayos del Sol se difunden en forma de abanico; esto s�lo es fruto de la perspectiva. Observadas en perspectiva, las l�neas paralelas parecen convergentes; recuerden, por ejemplo, los ra�les que se pierden a lo lejos, o una larga avenida de �rboles.
No obstante, el que los rayos del Sol caigan sobre la Tierra en un haz paralelo, no quiere decir, ni mucho menos, que la sombra completa del dirigible sea igual a la longitud del mismo. Si examinamos la figura veremos que la sombra completa del dirigible en el espacio se reduce en direcci�n a la Tierra y que, por consiguiente, la sombra reflejada en la superficie de la Tierra debe ser m�s corta que el mismo dirigible: CD menor que AB.
Si se sabe la altura a que vuela el dirigible, puede calcularse la magnitud de esta diferencia. Supongamos que vuele a una altura de 1.000 m sobre la superficie terrestre. El �ngulo formado por las l�neas A C y BD ser� igual al �ngulo por el que se ve el Sol desde la Tierra; la magnitud de este �ngulo es conocida: tiene cerca de medio grado. Por otra parte, es sabido que cualquier objeto, visto bajo un �ngulo de medio grado dista del ojo observador 115 veces su di�metro. Es decir, el segmento MN (este segmento se ve desde la superficie terrestre bajo un �ngulo de medio grado) debe ser la ciento decimoquinta parte de AC. La magnitud de AC es mayor que la perpendicular bajada desde A a la superficie de la Tierra. Si el �ngulo comprendido entre la direcci�n de los rayos solares y la superficie terrestre es de 45�, AC (estando el dirigible a 1.000 m de altura) equivale a unos 1.400 m, y por consiguiente, el segmento MN es igual a
Pero la diferencia entre la longitud del dirigible y la de su sombra, es decir, el segmento MB, es mayor que MN, exactamente 1,4 veces mayor, porque el �ngulo MBD es casi de 450. Por consiguiente MB es igual a 12 x 1,4; o sea, casi 17 m.
Todo lo dicho se refiere a la sombra completa del dirigible, negra y precisa, y no a la llamada semisombra, d�bil y difuminada. Nuestros c�lculos muestran, entre otras cosas, que si en lugar del dirigible hubiera un peque�o globo de menos de 17 metros de di�metro, no dar�a sombra completa alguna; se ver�a s�lo una semisombra vaga.
Volver
7. Un problema con cerillas
El jugador de turno vaci� sobre la mesa su caja de cerillas, distribuy�ndolas en tres montones.
- �Se dispone usted a hacer hogueras? - bromearon los presentes.
- El rompecabezas ser� bas�ndose en cerillas - explic� -. Tenemos tres montoncitos diferentes. En ellos hay en total 48 cerillas. No le digo cu�ntas hay en cada uno, pero observen lo siguiente: si de primer mont�n paso al segundo tantas cerillas como hay en �ste luego del segundo paso al tercero tantas cerillas como hay en es tercero, y, por �ltimo, del tercero paso al primero tantas cerillas como existen ahora en ese primero, resulta que habr� el mismo n�mero de cerillas en cada mont�n. �Cu�ntas cerillas hab�a en cada mont�n al principio?
Soluci�n
El problema hay que resolverlo empezando por el final. Vamos a partir de que, hechas todas las mudanzas correspondientes, los montoncitos tienen un n�mero igual de cerillas. Ya que en esos cambios el n�mero total de cerillas no ha cambiado, ha quedado invariable (48), al terminar todas las mudanzas result� haber en cada mont�n 16 cerillas.
As�, pues, al terminar tenemos:
| mont�n I | mont�n II | mont�n III |
| 16 | 16 | 16 |
Inmediatamente antes de esto, se hab�an a�adido al primer mont�n de cerillas tantas cerillas como hab�a en �l; en otras palabras, el n�mero de cerillas de este mont�n se hab�a duplicado. Esto quiere decir que antes de hacer el �ltimo cambio, en el primer mont�n no hab�a 16 cerillas, sino 8. En el tercero, del cual quitamos 8 cerillas hab�a, antes de hacer esta operaci�n. 16+8 = 24 cerillas
Las cerillas est�n ahora distribuidas por los montones as�:
|
mont�n I
8 |
mont�n II
16 |
mont�n III
24 |
Sigamos. Sabemos que antes de esto fueron pasadas desde el segundo mont�n al tercero tantas cerillas como hab�a en �ste: es decir, que el n�mero 24 es el doble de las cerillas existentes en el mont�n tercero antes de este cambio. De ah� deducimos la distribuci�n de las cerillas despu�s de la primera mutaci�n:
|
mont�n I
8 |
mont�n II
16+12=28 |
mont�n III
12 |
Es f�cil darse cuenta de que antes de hacer el primer cambio (es decir, antes de pasar del primer mont�n al segundo tantas cerillas como hab�a en �ste), la distribuci�n de las cerillas era la siguiente:
|
mont�n I
22 |
mont�n II
14 |
mont�n III
12 |
Este era el n�mero de cerillas que hab�a al principio en cada uno de los montones.
Volver
8. El toc�n traicionero
- Este rompecabezas - empez� a decir el pen�ltimo contertuliano - me recuerda un problema que me plante� en cierta ocasi�n un matem�tico rural. Era un cuento bastante divertido. Un campesino se encontr� en el bosque a un anciano desconocido. Pusi�ronse a charlar. El viejo mir� al campesino con atenci�n y le dijo:
- En este bosque s� yo de un toc�n maravilloso. En caso de necesidad ayuda mucho.
- �C�mo que ayuda! �Acaso cura algo?
- Curar no cura, pero duplica el dinero. Pones debajo d e �l el portamonedas con dinero, cuentas hasta cien, y listo: el dinero que hab�a en el portamonedas se ha duplicado. Esta es la propiedad que tiene. �Magn�fico toc�n!
- Si pudiera probar... exclam� so�ador el campesino. Es posible. �C�mo no! Pero hay que pagar.
- �Pagar? �A qui�n? �Mucho?
- Hay que pagar al que indique el camino. Es decir, a m� en este caso. Si va a ser mucho o poco es otra cuesti�n.
Empezaron a regatear. Al saber que el campesino llevaba poco dinero, el viejo se conform� con recibir una peseta y veinte c�ntimos despu�s de cada operaci�n.
El viejo condujo al campesino a lo m�s profundo del bosque, lo llev� de un lado para otro y por fin encontr� entre unas malezas un viejo toc�n de abeto cubierto de musgo. Tomando de manos del campesino el portamonedas, lo escondi� entre las ra�ces del toc�n.
Contaron hasta cien. El viejo empez� a escudri�ar y hurgar al pie del tronco, y al fin sac� el portamonedas, entreg�ndoselo al campesino.�ste mir� el interior del portamonedas y... en efecto, el dinero se hab�a duplicado. Cont� y dio al anciano la peseta y los veinte c�ntimos prometidos y le rog� que metiera por segunda vez el portamonedas bajo el toc�n.
Contaron de nuevo hasta cien; el viejo se puso otra vez a hurgar en la maleza junto al toc�n, y realiz�se el milagro: el dinero del portamonedas se hab�a duplicado. El viejo recibi� la peseta y los veinte c�ntimos convenidos.
Escondieron por tercera vez el portamonedas bajo el toc�n. El dinero se duplic� esta vez tambi�n. Pero cuando el campesino hubo pagado al viejo la remuneraci�n prometida, no qued� en el portamonedas ni un solo c�ntimo. El pobre hab�a perdido en la combinaci�n todo su dinero. No hab�a ya nada que duplicar y el campesino, abatido, se retir� del bosque.
El secreto de la duplicaci�n maravillosa del dinero, naturalmente, est� claro para ustedes: no en balde el viejo, rebuscando el portamonedas, hurgaba en la maleza junto al toc�n. Pero, �pueden ustedes indicar cu�nto dinero ten�a el campesino antes de los desdichados experimentos con el traicionero toc�n?
Soluci�n
Tambi�n es m�s sencillo resolver este rompecabezas empezando por el final. Sabemos que despu�s de la tercera duplicaci�n quedaron en el portamonedas una peseta y veinte c�ntimos (�ste fue el dinero que recibi� el viejo la �ltima vez). �Cu�nto hab�a antes de 16 esta operaci�n? Est� claro que sesenta c�ntimos. Estos c�ntimos hab�an quedado despu�s de pagar al viejo por segunda vez; una peseta y veinte c�ntimos; habiendo en el portamonedas, antes de pagarle, 1 peseta y 20 c�ntimos + 60 c�ntimos = 1 peseta y 80 c�ntimos.
Esta cantidad result� haber en el portamonedas despu�s de la segunda duplicaci�n: antes de ella hab�a s�lo 90 c�ntimos, que hab�an quedado despu�s de haber abonado al viejo por primera vez 1 peseta y 20 c�ntimos. De aqu� deducimos que en el portamonedas, antes de pagarle, hab�a 90 c�ntimos + 1 peseta y 20 c�ntimos = 2 pesetas
En el portamonedas hab�a ese dinero despu�s de la primera duplicaci�n; anteriormente hab�a la mitad; es decir, 1 peseta y 5 c�ntimos. Comprob�moslo.
Dinero en el portamonedas:
Despu�s de la primera duplicaci�n:
1 peseta 5 c�ntimos x 2 = 2 pesetas 10 c�ntimos
Despu�s del pago 1�:
2 pesetas 10 c�ntimos - 1 peseta 20 c�ntimos = 90 c�ntimos
Despu�s de la 2� duplicaci�n:
90 c�ntimos x 2 = 1 peseta 80 c�ntimos
Despu�s del pago 2�:
1 peseta 80 c�ntimos - 1 peseta 20 c�ntimos = 60 c�ntimos
Despu�s de la 3� duplicaci�n:
60 c�ntimos x 2 = 1 peseta 20 c�ntimos
Despu�s del pago 3�:
1 peseta 20 c�ntimos - 1 peseta 20 c�ntimos = 0 c�ntimos
Volver
9. Un truco aritm�tico
- Me toca hablar el �ltimo. A fin de que haya mayor variedad, presentar� un truco aritm�tico, con el ruego de que descubran el secreto que encierra. Que cualquiera de los presentes, usted mismo, presidente, escriba en un papel un n�mero de tres cifras, sin que yo lo vea.
- �El n�mero puede tener ceros?
- No pongo limitaci�n alguna. Cualquier n�mero de tres cifras, el que deseen.
- Ya lo he escrito. �Qu� m�s?
- A continuaci�n de ese mismo n�mero, escr�balo otra vez, y obtendr� una cantidad de seis cifras.
- Ya est�.
- D�le el papel al compa�ero m�s alejado de m�, y que este �ltimo divida por 7 la cantidad obtenida.
- �Qu� f�cil es decir div�dalo por siete! A lo mejor no se divide exactamente.
- No se apure; se divide sin dejar resto.
- No sabe usted qu� n�mero es, y asegura que se divide exactamente.
- Haga primero la divisi�n y luego hablaremos.
- Ha tenido usted la suerte de que se dividiera.
- Entregue el cociente a su vecino, sin que yo me entere de cu�l es, y que �l lo divida por 11.
- �Piensa usted que va a tener otra vez suerte, y que va a dividirse?
- Haga la divisi�n. No quedar� resto.
- �En efecto! �Y ahora, qu� m�s?
- Pase el resultado a otro. Vamos a dividirlo por... 13.
- No ha elegido bien. Son pocos los n�meros que se dividen exactamente por trece... �Oh, la divisi�n es exacta! �Qu� suerte tiene usted!
- D�me el papel con el resultado, pero d�blelo de modo que no pueda ver el n�mero.
Sin desdoblar la hoja de papel, el prestidigitador la entreg� al presidente.
- Ah� tiene el n�mero que usted hab�a pensado. �Es �se?
- �El mismo! - contest� admirado, mirando el papel - . Precisamente es el que yo hab�a pensado... Como se ha agotado la lista de jugadores, perm�tanme terminar nuestra reuni�n, sobre todo teniendo en cuenta que la lluvia ha cesado. Las soluciones de todos los rompecabezas se har�n p�blicas hoy mismo, despu�s de cenar. Las soluciones por escrito pueden entreg�rmelas a m�.
Antes de poner fin al cap�tulo de los rompecabezas en el albergue, explicar� tres trucos aritm�ticos m�s para que puedan ustedes entretener a sus amigos en los ratos libres. Dos de estos trucos consisten en averiguar n�meros; el tercero en averiguar cu�les son los propietarios de objetos determinados.
Son trucos viejos, y hasta es posible que los conozcan, pero no todos seguramente saben en qu� se basan. Para que el truco pueda presentarse en forma segura y racional, se requieren ciertos conocimientos te�ricos. Los dos primeros exigen una peque�a y nada fatigosa incursi�n por el �lgebra elemental.
Soluci�n
Analicemos lo que se ha hecho con el n�mero pensado. Ante todo, se le ha agregado detr�s el n�mero dado de tres cifras. Es lo mismo que agregarle tres ceros y luego sumarle el n�mero inicial; por ejemplo:
872.872 = 872.000 + 872
Se ve claro qu� es lo que en realidad se ha hecho con el n�mero: se ha aumentado 1.000 veces y adem�s se ha a�adido el mismo n�mero; en resumidas cuentas, hemos multiplicado el n�mero por 1.001.
�Qu� se ha hecho despu�s con el producto? Lo han dividido por 7, por 11 y por 13. Es decir, lo han dividido por el producto de 7 x 11 x 13, o lo que es lo mismo, por 1.001. . As�, pues, el n�mero pensado, primero lo han multiplicado por 1.001 y luego lo han dividido entre 1.001. �Cabe admirarse de que se haya obtenido el mismo n�mero?
Volver
10. La cifra tachada
Una persona piensa un n�mero de varias cifras, por ejemplo el 847. Prop�ngale que halle la suma de los valores absolutos de las cifras de, este n�mero (8 + 4 + 7 = 19) y que la reste del n�mero pensado. Le resultar�:
847 - 19 = 828
Que tache una cifra cualquiera del resultado obtenido, la que desee, y que le comunique a usted las restantes. Le dir� usted inmediatamente la cifra tachada, aunque no sepa el n�mero pensado y no haya visto lo que ha hecho con �l.
Soluci�n
�En qu� forma se hace esto y en qu� consiste la clave del truco?
La soluci�n es muy f�cil. Se busca una cifra que adicionada a las que le comunica su interlocutor forme el n�mero m�s pr�ximo divisible por 9. Si, por ejemplo, en el n�mero 828 ha sido tachada la primera cifra (8) y le comunican a usted las cifras 2 y 8, usted, una vez sumados 2 + 8, calcula que hasta el n�mero m�s pr�ximo divisible por 9, es decir, hasta el 18, faltan 8. Esta es la cifra tachada.
�Por qu� resulta as�? Porque si a cualquier n�mero le restamos la suma de sus cifras, debe quedar un n�mero divisible por 9; en otras palabras, un n�mero en el que la suma de los valores absolutos de sus cifras se divida por 9. En efecto, representemos por a la cifra de las centenas del n�mero pensado, por b la de las decenas y por c la de las unidades. Este n�mero tendr� en total:
Rest�mosle la suma de los valores de sus cifras a + b + c. Obtendremos:
Pero 9(11a + b) est� claro que es divisible por 9; por lo tanto, al restar de un n�mero la suma de los valores de sus cifras, debe resultar siempre un n�mero divisible por 9, sin residuo.
Al presentar el truco, puede suceder que la suma de las cifras que le comuniquen sea divisible entre nueve (por ejemplo 4 y 5). Esto indica que la cifra tachada es o un cero o un nueve. As�, que debe usted responder cero o nueve.
He aqu� una variante nueva del mismo truco: en lugar de restar del n�mero pensado la suma de los valores de sus cifras, puede restarse otro, formado cambiando de lugar las cifras de dicho n�mero. Por ejemplo, del n�mero 8.247 puede restarse 2.748 (si el n�mero nuevo es mayor que el pensado, se resta del mayor el menor). Luego se contin�a como se ha indicado anteriormente: 8.247 - 2.748 = 5.499; si se ha tachado la cifra 4, conociendo @las cifras 5, 9, 9, calcula usted que el n�mero divisible por 9 m�s pr�ximo a 5 + 9 + 9, es decir, a 23, es el n�mero 27. 0 sea, que se ha tachado la cifra 27 - 23 = 4.
Volver
11. Adivinar un n�mero sin preguntar nada
Propone usted a alguien que piense un n�mero cualquiera de tres cifras que no termine en cero, y le ruega que ponga las cifras en orden contrario. Hecho esto, debe restar del n�mero mayor el menor y la diferencia obtenida sumarla con ella misma, pero con las cifras escritas en orden contrario. Sin preguntar nada, adivina usted el n�mero resultante.
Soluci�n
Si, por ejemplo, se hab�a pensado el n�mero 467, deben realizarse las siguientes operaciones:
| 467; 764 |
764
-467
297 |
297
-792
1089 |
Este resultado final, 1.089, es el que comunica usted. �C�mo puede saberlo?Analicemos el problema en su aspecto general. Tomemos un n�mero con las cifras a, b y c. El n�mero ser�:
El n�mero con las cifras en orden contrario ser�:
La diferencia entre el primero y el segundo ser� igual a
Hagamos las siguientes transformaciones:
= 100 (a - c) - 100 + 100 - 10 + 10 - a + c =
=100 (a - c - 1) + 90 + (10 - a + c).
Es decir, que la diferencia consta de las tres cifras siguientes:
decenas: 9
unidades: 10 + c - a
El n�mero con las cifras en orden contrario se representa as�:
Sumando ambas expresiones:
Resulta:
Cualesquiera que sean las cifras a, b, c, una vez hechas las operaciones mencionadas se obtendr� siempre el mismo n�mero: 1.089. Por ello no es dif�cil adivinar el resultado de estos c�lculos: lo conoc�a usted de antemano.
Est� claro que este truco no debe presentarse a la misma persona dos veces porque entonces el secreto quedar� descubierto.
Volver
12. �Qui�n ha cogido cada objeto?
Para presentar este ingenioso truco, @hay que preparar tres cosas u objetos peque�os que quepan f�cilmente en el bolsillo, por ejemplo, un l�piz, una llave y un cortaplumas. Adem�s, se coloca en la mesa un plato con 24 avellanas; a falta de ellas pueden utilizar fichas del juego de damas, de domin�, cerillas, etc�tera.
A tres de los presentes les propone que mientras est� usted fuera de la habitaci�n, escondan en sus bolsillos, a su elecci�n, uno cualquiera de los tres objetos: el l�piz, la llave o el cortaplumas, y se compromete usted a adivinar el objeto que ha escondido cada uno.
El procedimiento para adivinarlo consiste en lo siguiente: Al regresar a la habitaci�n una vez que las tres personas hayan escondido los objetos en los bolsillos, les entrega usted unas avellanas para que las guarden. Al primero le da una avellana, dos al segundo y tres al tercero. Las restantes las deja en el plato. Luego sale usted otra vez dej�ndoles las siguientes instrucciones: cada uno debe coger del plato m�s avellanas; el que tenga el l�piz tomar� tantas como le fueron entregadas; el que tenga la llave, el doble de las que recibi�; el del cortaplumas, cuatro veces m�s que las que usted le haya dado.
Las dem�s avellanas quedan en el plato.
Una vez hecho todo esto y dada la se�al de que puede regresar, al entrar en el cuarto echa usted una mirada al plato, e inmediatamente anuncia cu�l es el objeto que cada uno guarda en el bolsillo.
Soluci�n
El truco deja perplejo al p�blico, sobre todo porque se realiza sin participaci�n de intermediarios secretos que nos hagan se�ales imperceptibles convenidas previamente. Es un truco sin enga�o alguno, pues todo �l est� fundamentado exclusivamente en c�lculos aritm�ticos. Se adivina qui�n tiene cada objeto, s�lo por el n�mero de avellanas que han quedado en el plato. Quedan siempre pocas: de 1 a 7, y pueden contarse de un solo golpe de vista.
Pero, �c�mo conocer qui�n ha guardado uno u otro objeto, por el n�mero de avellanas que quedan?
Es muy sencillo; cada caso de distribuci�n de los objetos entre las tres personas corresponden a un n�mero diferente de avellanas del plato. Vamos a convencernos inmediatamente.
Supongamos que sus compa�eros se llaman Benigno, Gregorio y Juan. Design�mosles por sus iniciales: B, G, J. Designemos tambi�n los objetos por letras: el l�piz a, la llave b y el cortaplumas c. �C�mo pueden distribuirse estos objetos entre tres personas? De las seis maneras siguientes:
|
B
a a b b c c |
G
b c a c a b |
J
c b c a b a |
Es evidente que no puede haber m�s combinaciones; la tabla comprende todas las posibles.Veamos ahora qu� n�mero de avellanas quedan en el plato en cada uno de los casos:
| BGJ | N�mero de avellanas tomadas | Total | Resto | ||
|
abc
acb bac bca cab cba |
1+1=2
1+1=2 1+2=3 1+2=3 1+4=5 1+4=5 |
2+4=6
2+8=10 2+2=4 2+8=10 2+2=4 2+4=6 |
3+12=15
3+6=9 3+12=15 3+3=6 3+6=9 3+3=6 |
23
21 22 19 18 17 |
1
2 3 5 6 7 |
Ya ven que el resto de avellanas es diferente cada vez. Por ello, conociendo el resto, es f�cil determinar c�mo est�n distribuidos los objetos entre sus amigos. De nuevo -por tercera vez- se aleja de la habitaci�n y mira su libretita de notas donde lleva apuntado el cuadro anterior (en realidad s�lo hacen falta la primera y la �ltima columna); es dif�cil recordarlo de memoria, y adem�s no hay necesidad de ello. El cuadro le indicar� d�nde se halla cada objeto. Por ejemplo, si han quedado en el plato 5 avellanas, quiere decir (caso bca) que
|
la llave la tiene Benigno;
el cortaplumas, Gregorio; el l�piz, Juan. |
Para que el truco salga bien, debe recordar exactamente cu�ntas avellanas ha entregado a cada persona (distrib�yalas siempre siguiendo el orden alfab�tico de los nombres, como lo hemos hecho en el caso explicado).
Volver