|
Une réflexion sur les programmes de mathématiques dans le secondaire.
(par des collègues du lycée de Franconville, Val
d'Oise.)
Un nouveau programme de Seconde entrera en vigueur à la rentrée
2000. Éminemment critiquable, il ne fait cependant que reprendre et accentuer
des tendances nettement perceptibles depuis plusieurs années.
Nous avons relevé certains aspects de cette évolution en étudiant
quelques exemples assortis de commentaires.
Les passages en italiques sont extraits des programmes officiels.
1. La chasse à l'abstraction.
1.1. Les mathématiques s'appuient sur la logique, et, depuis maintenant un
siècle, sur la théorie des ensembles. Rien de tout cela dans les programmes
de mathématiques de l'an 2000. Quelle est la négation de :

ou :

Les implications ? " Conduire vers la maîtrise d'un vocabulaire logique
adapté " suffira amplement. Les intersections et les réunions
? Inutile ! Il s'agit pourtant là de notions dont l'intérêt déborde
largement du seul cadre des mathématiques, et dont les élèves
pourraient tirer profit dans bien d'autres disciplines.
1.2. Plus question d'étudier et de comparer les propriétés des
opérations. Depuis longtemps déjà, on ne parle plus de commutativité,
d'associativité, mots barbares et concepts inutiles censés semer la
confusion dans les esprits. Demandez à un élève de seconde de
calculer :

ou :
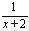
sachant que :

(car il va prendre sa calculatrice)...
1.3. Des pans entiers du programme doivent être traités sous forme
d'exemples ou en travaux pratiques, et, nouvelle mode, en " thèmes d'étude
". Bien sûr des exercices d'approche ou d'application sont très
utiles pour aider l'élève à assimiler une notion nouvelle. Cependant,
en l'absence d'un minimum de formalisation, il y a lieu de craindre que les élèves
ne retiennent que des " recettes de cuisine " ou se livrent à des
généralisations hasardeuses. Faites développer :
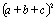 à un
élève de seconde... à un
élève de seconde...
2. Plus de démonstrations.
2.1. Démontrer est une activité essentielle du mathématicien.
Or, les démonstrations ont une fâcheuse tendance à disparaître
de l'enseignement secondaire.
2.2. C'est déjà le cas en collège. Il ne reste pratiquement
plus qu'une " démonstration " du théorème de Pythagore
utilisant les aires.
2.3. D'ailleurs, on ne comprend pas la différence entre le théorème
et sa réciproque ? Qu'à cela ne tienne : il n'y a qu'à faire
un paquet et l'appeler " la propriété de Pythagore ", valable
dans les deux sens.
2.4. Plus généralement, les élèves ne comprenaient
pas les implications, les interprétaient comme des équivalences ou
les confondaient avec leur réciproque. Pas étonnant, ils n'avaient
jamais reçu de notions de logique. Mesure prise: interdiction de l'utilisation
du symbole d'implication :

Les théorèmes seraient désormais énoncés sous
la forme " Si..., alors... ". Les élèves n'ont pas mieux
compris. Les éditeurs ont emboîté le pas. On a alors décidé
d'énoncer les théorèmes sous la forme " Si l'on sait que...,
alors on peut en déduire que... ". Les élèves n'ont toujours
pas compris. On a alors décidé d'énoncer les théorèmes
sous la forme " Si l'on sait, grâce à l'énoncé ou
parce qu'on l'a démontré auparavant que..., alors on peut affirmer
que... ". Après, c'est devenu trop compliqué, alors on a abandonné.
2.5. Or il est possible de faire des démonstrations avec les élèves
: il suffit par exemple de partir d'un système d'axiomes enrichi, et de démontrer
les théorèmes qui en découlent.
2.6. Montrer que les médiatrices d'un triangle sont concourantes, c'est vraiment
si difficile que cela ?
3. Les contenus.
3.1. L'Arithmétique en cinquième. Les élèves comprenaient,
participaient, avaient de bonnes notes. Au milieu de l'année, cela permettait
d'en remobiliser certains qui avaient décroché. Cela leur était
utile plus tard pour les calculs de fractions (au lieu de faire bêtement le
produit des dénominateurs).
3.2. Aujourd'hui, c'est l'Analyse qui a la part belle. Tout phénomène
doit pouvoir " entrer " dans une fonction (dont on aura seulement une "
notion "). Il faut donc bien savoir les étudier, sans trop entrer dans
la complexité. S'en tenir à de rapides considérations du genre
" ça monte et ça descend ", pour bien comprendre le journaliste
de 20 heures. L'essentiel est que ça tienne sur un écran de calculatrice
ou dans les cellules d'un tableur, dont on se gardera de critiquer les erreurs d'affichage
ou d'arrondi. C'est ainsi que les angles orientés, les équations de
droites, et les homothéties disparaissent du programme de seconde. Il ne reste
plus de Géométrie digne de ce nom que dans les sections scientifiques,
et encore, seulement en spécialité pour les TS, après avoir
amputé les coniques : on en parlera avec les courbes paramétrées
!
3.3. Personne ne nie l'intérêt de savoir correctement interpréter
des données statistiques. Est-ce une raison pour passer l'un des " trois
grands chapitres " de la classe de seconde à " réfléchir
au choix de résumés numériques ", à " la notion
de fluctuation de l'échantillonnage vue sous l'aspect élémentaire
de la variabilité de la distribution des fréquences " (sic), tout
cela pour finir en apothéose par " simuler à l'aide du générateur
aléatoire d'une calculatrice " ?!?
3.4. Même en spécialité de TL ! Des littéraires qui choisissent
de faire des maths ! On pourrait profiter de l'occasion pour leur faire découvrir
l'histoire de la racine carrée de -1, la résolution des équations
dans :
 , ,
ou les motifs du carrelage de la cuisine de Pascal. Non, ils étudieront les
variations des fonctions, comme les autres.
4. L'obsession du " simple ".
" On prendra un point de vue très simple ", " on se limitera
à de faibles valeurs de n ", " l'objectif est modeste ", "
toute théorie est exclue ", " on ne soulèvera pas de difficulté
", " la notion sera dégagée de l'étude d'exemples
simples ", " des exemples simples " (x fois...), " on n'utilisera
le calcul vectoriel que pour faciliter le repérage des points ", "
on se gardera de tout excès de technicité ", " un cadre théorique
volontairement limité ",...
Sans commentaires.
5. La dilution d'une notion sur plusieurs années.
5.1. Prenons l'exemple des fractions: on en parle en primaire, on les simplifie en
sixième, on les compare, les ajoute et les multiplie en cinquième,
et on ne sait pas quand on les divise. L'intention était d'éviter un
" chapitre trop long ", et de permettre aux élèves
" qui ne peuvent se faire aider " d'assimiler à leur rythme chaque
notion avant de passer à la suivante. Le problème, c'est que, à
partir du moment où ils en parlent à la maison, les élèves
" qui peuvent se faire aider ", apprennent tout sur la question et
ainsi la belle intention d'égalité est ruinée.
5.2. On observe la même dilution pour les statistiques au collège.
6. La fin de la rigueur.
6.1. Des fonctions peuvent être " définies par des courbes ",
on observe " les effets d'un agrandissement ", des triangles ont "
la même forme "...
6.2. Comment peut-on démontrer que deux droites sont parallèles en
utilisant le théorème de Thalès si l'on ne sait pas que "
la position de M par rapport à A et B est la même que celle de N par
rapport à A et C " ? Où et quand cette expression a-t-elle été
définie correctement ?
6.3. Qu'est-ce qu'un vecteur ? Et comment reconnaît-on que deux vecteurs ont
le " même sens " ?
6.4. De quoi découle la position relative de deux plans de l'Espace? De la
" manipulation de solides " ? De la " construction de patrons "
?
7. Et pourtant.
7.1. Les élèves manifestent un vif intérêt pour des situations
" non-standard ". La leçon d'introduction aux nombres complexes
en Terminale en témoigne régulièrement.
7.2. Les élèves de premières ES, auxquels on inflige des "
mathématiques appliquées aux sciences économiques ", redoutent
les exercices " concrets ". Ils préfèrent encore les x et
les y. Les modèles adoptés, souvent artificiels, sont d'ailleurs souvent
critiqués par les professeurs de SES eux-mêmes.
7.3. Il n'y a donc pas de fermeture " naturelle " des esprits à
l'abstraction, et les mathématiques ne sont pas " naturellement "
le lieu d'étude de phénomènes " concrets ". Tout est
question d'éducation...
Ainsi, l'objectif des programmes de mathématiques depuis plusieurs années
est clair: la recherche de l'utilité immédiate au détriment
de la réflexion, la réduction des mathématiques à une
technique, à une accumulation de recettes applicables aux autres disciplines.
La négation du sens de l'effort et de la pensée...
C'est exactement ce qu'il faut pour la société qu'on nous prépare.
|