C O N T E N I D O
Aclaraciones
Citas
1. Introducción
2. Zenón, Eudoxio y Arquímedes
3. Descartes
4. Fermat
5. Pascal
6. Newton
7. Leibniz
8. Los Bernoulli
9. Euler
10. Lagrange
11. Laplace
12. Monge y Fourier
13. Poncelet
14. Gauss
15. Cauchy
16. Lobatchewsky
17. Abel
18. Jacobi
19. Hamilton
20. Galois
21. Silvester
22. Weierstrass y Sonja Kowalewsky
23. Boole
24. Hermite
25. Kronecker
26. Riemann
27. Kummer y Dedekind
28. Poincaré
29. Cantor
Bajar Parte 1
Bajar Parte 2
Bajar Parte 3
ANIMA CANDIDA
RIEMANN
|
Un geómetra como Riemann pudo casi haber previsto las características más
importantes del mundo actual.
A. S. Eddington |
Refiriéndose a Coleridge, se ha dicho que escribió poca poesía de primer orden, pero que esa poca está hecha de oro. Lo mismo podría decirse de Bernhard Riemann, cuyos frutos matemáticos apenas bastan para llenar un volumen en octavo. También podría decirse que Riemann revolucionaba todo aquello que tocaba. Uno de los matemáticos más originales de los tiempos modernos, Riemann, heredó por desgracia una precaria constitución, y murió antes de que madurase una décima parte de la dorada cosecha de su fértil cerebro. Si hubiera nacido un siglo más tarde, es probable que la ciencia médica hubiera sido capaz de alargar su vida veinte o treinta años y la Matemática no hubiera tenido que esperar la aparición de un sucesor.
Georg Friedrich Bernhard Riemann, hijo de un pastor luterano, el segundo de seis hermanos (dos hermanos y cuatro hermanas), nació en la pequeña aldea de Breselenz, en Hanover, Alemania, el 17 de septiembre de 1826. Su padre combatió en las guerras napoleónicas, y cuando abandonó este modo de vivir por otro menos bárbaro, se casó con Charlotte Ebell hija de un modesto abogado. En el año 1826, Hanover no gozaba de una vida próspera, y las condiciones de un oscuro pastor con una mujer y seis hijos que alimentar y vestir no eran en realidad envidiables. Algunos biógrafos pretenden, quizá con justicia, que la delicada salud y las muertes prematuras de muchos de los hijos de Riemann fueron el resultado de la desnutrición de su juventud, y no debidas a circunstancias realmente ingentes. La madre murió también antes de que sus hijos llegaran a la edad adulta.
A pesar de la pobreza, la vida de su hogar era feliz, y Riemann siempre mantuvo el más cálido afecto, y una intensa nostalgia cuando estaba ausente, para toda su cariñosa familia. Desde sus primeros años fue un alma tímida y desconfiada, con un terrible horror ante la idea de hablar en público o de atraer la atención sobre sí mismo. En su vida posterior esta crónica timidez constituyó un serio obstáculo, ocasionándole muchos tormentos, hasta que pudo vencerla por una diligente preparación cuando tenía que hacer una presentación en público. La simpática timidez de la infancia y de la adolescencia de Riemann atraía a todo el que le conoció, y estaba en extraño contraste con la audacia de su pensamiento científico maduro. Reconociéndose supremo en el mundo de su propia creación, se daba cuenta de su transcendental capacidad, y no temía a nadie, real o imaginario.
Siendo todavía niño, el padre pasó al curato de Quickborn. Allí, el joven Riemann recibió de su padre, que parecía ser un excelente maestro, su primera instrucción. Desde las primeras lecciones Bernhard mostró un deseo insaciable de aprender. Las primeras cosas que le interesaron fueron las históricas, particularmente la trágica y romántica historia de Polonia. Cuando tenía cinco años Bernhard no dejaba en paz a su padre, pidiéndole que le narrara una y otra vez la leyenda de las luchas heroicas, y algunas veces ligeramente fatuas, de la infeliz Polonia, por la libertad y por la "autodeterminación", empleando la significativa frase de Woodrow Wilson.
La Aritmética, cuyo estudio comenzó a los 6 años, dio lugar a que se revelara pronto su ingénito genio matemático. Bernhard no sólo resolvía todos los problemas que se le presentaban, sino que inventaba casos más difíciles para exasperar a sus hermanos y hermanas. Ya el impulso creador en la Matemática dominaba la mente del muchacho. Teniendo 10 años comenzó a recibir lecciones de Aritmética y Geometría superior de un maestro profesional, un tal Schulz, que parecía buen pedagogo. Schulz pronto se encontró por debajo de su discípulo, que con frecuencia obtenía mejores soluciones que él.
A los 14 años Riemann fue a vivir con su abuela a Hanover, donde ingresó en la escuela secundaria, en el tercer grado superior. Aquí comenzó a sentir por primera vez su soledad. Su timidez hacía de él el blanco de las bromas de sus compañeros, y ello le impulsó a concentrarse sobre sí mismo. Después de un retroceso temporal, su comportamiento en el Instituto fue excelente, pero él no se permitía lujo alguno, y su único solaz era la compra de algunos pequeños regalos, adquiridos con sus ahorros, para enviarlos a sus padres, hermanos y hermanas en los días de sus cumpleaños. En una ocasión inventó y preparó como regalo para sus padres un calendario perpetuo muy original, que produjo el asombro de sus incrédulos compañeros. A la muerte de su abuela, dos años más tarde, Riemann fue llevado al Instituto de Lüneburg, donde estudió hasta que logró la preparación necesaria para ingresar en la Universidad de Göttingen, teniendo 19 años. Lüneburg estaba cerca del hogar de Riemann, quien aprovechaba así todas las oportunidades para poder gozar del calor de su casa. Estos años de educación secundaria, cuando su salud era aún buena, fueron los más felices de su vida. Los viajes de ida y vuelta entre el Instituto y Quickborn exigían un esfuerzo a su salud, pero, a pesar de las angustias de la madre, Riemann continuó realizando estos excesos para poder estar con su familia el mayor tiempo posible.
Cuando todavía estaba en el Instituto, Riemann tenía ya el prurito por la perfección, que más tarde habría de demorar sus publicaciones científicas. Este defecto, si lo es, le causó grandes dificultades en sus ejercicios escritos, y al principio hasta pareció dudoso que pudiera triunfar en sus exámenes. Pero este mismo rasgo fue más tarde, la causa de la forma acabada de dos de sus obras maestras, una de las cuales fue considerada por Gauss como perfecta. Más tarde las cosas mejoraron, cuando Seyffer, el maestro de hebreo, recibió a Riemann en su propia casa como pupilo.
Los dos estudiaron juntos hebreo. Riemann hacía más de lo que podía, pues el futuro matemático deseaba en aquellos días satisfacer los deseos de su padre y ser un gran predicador, como si el pobre Riemann, con su timidez, pudiera haber subido al púlpito para desafiar al infierno y hablar de la condenación, o de la redención en el Paraíso. El mismo Riemann estaba satisfecho con sus piadosos planes, y aunque jamás preparó un sermón, empleó sus talentos matemáticos para intentar la demostración, a la manera de Spinoza, de la verdad del Génesis. Sin importarle su fracaso, el joven Riemann conservó su fe, y continuó siendo toda su vida un sincero cristiano. Como su biógrafo (Dedekind) afirma: "Evitó reverentemente alterar la fe de los demás; para él lo principal en la religión era el autoexamen diario". Al terminar el curso de la Escuela secundaria todos estaban conformes, hasta el propio Riemann, de que el Todopoderoso no podría utilizarlo para derrotar al demonio, pero podría emplearle provechosamente para la conquista de la naturaleza. Así, una vez más, como en los casos de Boole y Kummer, ad majoram Dei gloriam.
Habiendo observado el director del Instituto, Schmalfuss, el talento de Riemann para la Matemática, le permitió entrar en su biblioteca privada, librándole de asistir a la clase de Matemática. De esta forma Riemann descubrió sus aptitudes ingénitas para esta ciencia, pero su incapacidad para darse cuenta inmediatamente de la magnitud de su talento es tan característico de su casi patológica modestia que resulta ridículo.
Schmalfuss sugirió a Riemann la idea de que retirara algún libro matemático de la biblioteca, para que lo estudiara en su casa, y a Riemann le pareció excelente la idea con tal de que el libro no fuera demasiado fácil. Por indicación de Schmalfuss eligió la Théorie des Nombres (Teorías de números), de Legendre. Se trata, nada menos, que de una obra de 850 páginas, en cuarto mayor, y llena de razonamientos complicados. Seis días más tarde Riemann devolvió el libro. "¿Cómo ha podido leerlo tan pronto?" preguntó Schamalfuss. Sin contestar directamente, Riemann expresó su aprecio por la obra clásica de Legendre. "Es ciertamente un libro maravilloso. Lo he comprendido", y en efecto era verdad. Algún tiempo más tarde, al someterse al examen, respondió perfectamente, aunque hacía ya meses que no había vuelto a ver el libro.
No hay duda de que este es el origen de la afición de Riemann por el enigma de los números primos. Legendre tiene una fórmula empírica para calcular el número aproximado de primos menor que cualquier número dado. Una de las obras más profundas y más sugestivas de Riemann (aunque sólo tiene ocho páginas) se refiere al mismo tema general. En efecto, "la hipótesis de Riemann", que se origina en su ensayo para mejorar la obra de Legendre, es actualmente uno de los desafíos notables, si no el más notable, a los matemáticos puros.
Anticipándonos ligeramente a lo que luego diremos, podemos exponer aquí lo que es esta hipótesis. Se plantea en la famosa memoria de Ueber die Anzahl der Primzahlen unter einer gegebenen Grosse. (Sobre el número de números primos inferiores a uno dado) impresa en la publicación mensual de la Academia de Berlín, noviembre 1859, cuando Riemann tenía 33 años. El problema se refiere a encontrar una fórmula que dé los primos que existen menores que un número dado n. Al intentar resolver esta cuestión, Riemann fue llevado a una investigación de la serie infinita
en la que s es un número complejo, o sea s= u + iv , (
), donde
u
y
v
son números reales, elegidos de modo que la serie sea convergente. Con este
requisito, la serie infinita es una función de
s
, o sea
z
(s) (la zeta griega
z
, se usa siempre para denotar esta función que se llama "función zeta de
Riemann"); y como
s
varía,
z
(s) continuamente toma diferentes valores.
¿Para qué valores de s será
z
(
s
)
cero?
Riemann conjeturó que
todos
esos valores de
s
para los cuales
n
está entre 0 y 1 son de la forma
o sea que todos tienen su parte real igual a ½.
Esta es la famosa hipótesis. Pruebe o no pruebe algo, se cubrió de gloria, e incidentalmente resolvió muchas cuestiones extraordinariamente difíciles en la teoría de números primos, en otras partes de la Aritmética superior y en algunos campos del análisis. La opinión de los especialistas está en favor de la verdad de la hipótesis. En 1914, el matemático inglés G. H. Hardy demostró que una infinidad de valores de s satisface la hipótesis, pero una infinidad no es necesariamente todo. Una decisión de algún tipo que resuelva la conjetura de Riemann sería probablemente de mayor interés para los matemáticos que una prueba o un rechazo del último teorema de Fermat. La hipótesis de Riemann no es un tipo de problema que pueda ser abordado por métodos elementales. Ya ha dado lugar a una extensa y complicada bibliografía.
Legendre no fue el único gran matemático cuyas obras fueron comprendidas por Riemann, siempre con asombrosa rapidez cuando estaba en el Instituto. Se familiarizó con el Cálculo y sus ramificaciones a través del estudio de Euler. Es sorprendente que aunque su iniciación en el análisis fuera anticuada (los métodos de Euler estaban ya anticuados el año 1840 después de los trabajos de Gauss, Abel y Cauchy), llegara Riemann a ser un analista tan agudo. Pero de Euler tomó algo que también tiene su importancia en la obra matemática creadora. La apreciación de las formas simétricas y la inventiva para el tratamiento de las fórmulas. Aunque Riemann dependió principalmente en sus grandes inspiraciones de lo que pueden ser llamadas profundas ideas filosóficas, las que van al corazón de la teoría, su obra no carece, de todos modos, de esa "sencilla ingeniosidad" en la que Euler fue el maestro perfecto. La persecución de bellas fórmulas y de pulidos teoremas pueden, sin duda, degenerar rápidamente en un vicio estúpido, pero también pueden ir hacia la austera generalización, en un grado tal que las conclusiones sean tan generales que no puedan ser aplicadas a cualquier caso particular. El tacto matemático característico de Riemann impidió que cayera en los dos perniciosos extremos.
En 1846, teniendo 19 años, Riemann se matriculó como estudiante de filología y teología en la Universidad de Göttingen. Le animaba el deseo de agradar a su padre, y posiblemente ayudarle financieramente, obteniendo algún cargo retribuido tan pronto como le fuera posible. Pero no podía abstenerse de asistir a las conferencias matemáticas de Stern sobre la teoría de ecuaciones y sobre integrales definidas, a las de Gauss sobre el método de los mínimos cuadrados y a la de Goldschmidt sobre el magnetismo terrestre. Confesando todo a su indulgente padre, Riemann le pidió el permiso para desviar sus estudios. El padre consintió que Bernhard siguiera la carrera matemática, lo que produjo en el joven un sentimiento de profunda felicidad y agradecimiento.
Después de pasar un año en Göttingen,, donde la enseñanza era, sin duda, anticuada, Riemann marchó a Berlín para ser iniciado por Jacobi, Dirichlet, Steiner y Eisenstein, en nuevas y vitales Matemáticas. De todos estos maestros aprendió mucho, mecánica y álgebra superior de Jacobi, la teoría de números y análisis de Dirichlet, Geometría moderna de Steiner, mientras Eisenstein, que tenía tres años más que el discípulo le enseñó no sólo funciones elípticas, sino también confianza en sí mismo, pues él y el joven maestro tenían radicales diferencias de opinión acerca de cómo debían desenvolverse la teoría. Eisenstein insistía en establecer fórmulas bellas, a la manera de un modernizado Euler; Riemann deseaba introducir la variable compleja, y derivar toda la teoría, con un mínimo de cálculo, desde algunos simples principios generales. No hay duda de que así se originaron, al menos, los gérmenes de una de las más grandes contribuciones de Riemann a la Matemática pura. Como el origen de la obra de Riemann en la teoría de funciones de variable compleja es de considerable importancia para su propia historia y para la de las modernas Matemáticas examinaremos lo que se sabe acerca de esta cuestión.
La definición de una función analítica de una variable compleja, expuesta en relación con la anticipación de Gauss al teorema fundamental de Cauchy, fue esencialmente la de Riemann. Cuando se expresa analíticamente en lugar de geométricamente, esa definición se pone a la par de las ecuaciones en derivadas parciales, que Riemann tomó como punto de partida para una teoría de funciones de una variable compleja. Según Dedekind, "Riemann reconoció en esas ecuaciones diferenciales parciales la definición esencial de una función (analítica) de una variable compleja. Probablemente estas ideas, de suma importancia para su futura carrera, fueron elaboradas por Riemann en las vacaciones del otoño de 1847 (tenía 21 años)".
Otra versión del origen de la inspiración de Riemann es debida, a Sylvester, quien narra la siguiente historia, muy interesante, aunque posiblemente no sea cierta. En 1896, el año antes de su muerte, Sylvester recuerda que estaba en "un hotel sobre el río en Nuremberg, donde ,conversaba con un librero de Berlín, que iba a trasladarse, como yo, a Praga... Me dijo que había sido condiscípulo de Riemann en la Universidad, y que un día, después de haber recibido de París algunos números de las Comptes rendus, había permanecido aislado durante algunas semanas, y cuando volvió a la sociedad de sus amigos dijo (refiriéndose a los trabajos recientemente publicados por Cauchy): Esta es una nueva Matemática".
Riemann permaneció dos años en la ciudad de Berlín. Durante los movimientos políticos de 1848 permaneció con el cuerpo de estudiantes leales, y tuvo que hacer guardia durante 16 horas para proteger, en el palacio real, a la nerviosa y sagrada persona del rey. En 1849 volvió a Göttingen para completar sus conocimientos matemáticos y doctorarse. Los problemas que le interesaban eran de ordinario más amplios que lo que suelen interesar al matemático puro, y, en efecto, dedicó gran parte de su tiempo a la ciencia física, aparte de la Matemática.
Aunque el real interés de Riemann fuera la física matemática, parece muy posible que de haber vivido 20 6 30 años más hubiera llegado a ser el Newton o el Einstein del siglo XIX. Sus ideas en la física eran muy audaces para su época. Hasta que Einstein se dio cuenta del sueño de Riemann de una física geometrizada (macroscópica), la física que Riemann previó, quizá algo oscuramente, no pareció razonable a los físicos. En esta dirección su único continuador comprensivo hasta antes de nuestro siglo, fue el matemático inglés William Kingdon Cliffor (1845-1879).
Durante sus últimos tres semestres en Göttingen asistió a conferencias sobre filosofía y siguió con el mayor interés, el curso de Wilhelm Weber de física experimental. Los escritos fragmentarios filosóficos y psicológicos, encontrados después de la muerte de Riemann, muestran que como pensador y filósofo era tan original como en Matemática y ciencia. Weber reconoció el genio científico de Riemann, y fue su íntimo amigo y útil consejero. En un grado mucho mayor que la mayoría de los grandes matemáticos que han escrito sobre ciencia física, Riemann tenía una inclinación para lo que es importante o probablemente, lo será en física, y esa inclinación no hay duda de que era debida a su trabajo en el laboratorio y a su contacto con hombres que eran esencialmente físicos y no matemáticos. Las contribuciones de los más grandes matemáticos puros a la ciencia física han solido caracterizarse por una singular indiferencia para el universo observado por los hombres de ciencia. Riemann, como matemático físico, estaba en la misma categoría de Newton, Gauss y Einstein en su instinto para aquello que probablemente tendrá uso científico en Matemática.
Como una secuela a sus estudios filosóficos con Johann Friedrich Herbart (1776-1841), Riemann llegó a la conclusión, en 1850 (tenía 24 años), de que "puede ser establecida una teoría matemática completa que vaya desde las leyes elementales para los puntos individuales hasta los procesos que aparecen ante nosotros en el plenum ('espacio continuamente lleno') de la realidad, sin distinción entre gravitación, electricidad, magnetismo o termostática". Estas palabras probablemente pueden ser interpretadas como la repulsa de Riemann a toda teoría de la "acción a distancia" en la ciencia física, en favor de la teoría del campo. En las últimas las propiedades físicas del "espacio" que rodea una "partícula cargada" son el objeto de la investigación matemática. Riemann, en esta fase de su carrera, parece haber creído en un "éter" que llena el espacio, concepción ahora abandonada, pero, como se aprecia en su obra excepcional sobre los fundamentos de la Geometría, más tarde buscó la descripción y correlación de los fenómenos físicos en la Geometría del "espacio" de la experiencia humana. Es decir, rechaza, como en la moda actual, el éter inobservable, como algo superfluo que no hace más que embrollar.
Fascinado por sus trabajos en el campo de la física, Riemann abandonó el lado matemático puro durante cierto tiempo, y en el otoño de 1850 asistió al seminario de física matemática fundado por Weber, Ulrich, Stern, y Listing. Los experimentos físicos en este seminario consumieron el tiempo que podría haber reservado para la disertación doctoral en Matemática, que Riemann no emprendió hasta que tuvo 25 años.
Podemos recordar de pasada a uno de los directores del seminario Johann Benedict Listing (1808 - 1882), pues probablemente influyó sobre los pensamientos de Riemann para lo que había de ser (1857) una de sus grandes conquistas, la introducción de los métodos topológicos en la teoría de funciones de variable compleja.
Se recordará que Gauss profetizó que el análisis situs constituiría uno de los campos más importantes de la matemática, y Riemann, con sus invenciones en la teoría de funciones, iba a cumplir en parte esta profecía. Aunque la topología (antes llamada Análisis situs) que se desarrolló al principio poca semejanza tiene con la complicada teoría que actualmente absorbe todas las energías de una fecunda escuela puede ser de interés recordar el trivial enigma que, al parecer inició la vasta e intrincada teoría. En los tiempos de Euler existían siete puentes sobre el río Pregel, en Königsberg, como muestra la figura.
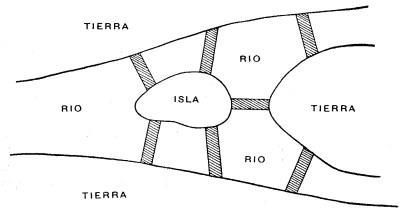
Euler propuso el problema de cruzar por los siete puentes sin pasar dos veces por algunos de ellos. El problema es imposible.
Podríamos exponer en este lugar la forma de usar los métodos topológicos de Riemann en la teoría de funciones, pero no hay manera de hacer una adecuada explicación en lenguaje no técnico. Para la significación de "uniformidad" con respecto a una función de una variable compleja debemos referirnos a lo dicho en el capítulo sobre Gauss. Ahora, en la teoría de funciones abelianas, se presentan inevitablemente funciones multiformes; una función de n valores de z es una función que, salvo para ciertos valores de z , toma precisamente n valores distintos para cada valor asignado a z . Ilustrando la multiformidad, o la polivalencia, para funciones de una variable real, notemos que y , considerada como una función de x , definida por la ecuación y 2 = x , tiene doble valor. Por tanto si x = 4, tenemos y 2 = 4, y por esto y = 2 ó - 2; si x es cualquier número real, salvo cero o "infinito", y tiene los dos distintos valores de
y -
. En este ejemplo, el más sencillo posible,
y
y
x
están relacionados por una ecuación algebraica, o sea
y
2
-
x
= 0. Pasando inmediatamente a la situación general, de la cual este es un caso
especial, discutiremos la función y de
n
valores, que se define como una función de x por la ecuación
en la cual las P son polinomios en x . Esta ecuación define y como una función de n valores de x . Como en el caso de y 2 - x = 0, existirán ciertos valores de x para los cuales dos o más de estos valores n de y son iguales. Estos valores de x son los llamados puntos de ramificación de la función de n valores definida por la ecuación.
Todo ésto se extiende ahora a funciones de variables complejas, y la función w (también su integral) definida por
en la cual z representa la variable compleja s + it, donde s , t son variables reales e i =
. Los valores
n
de
w
se llaman las
ramas
de la función
w
. Aquí debemos referirnos (capítulo sobre Gauss) a lo que se dijo acerca de la
representación de funciones
uniformes
de
z
. Supongamos que la variable
z
( =
s + it)
traza un camino en su plano, y supongamos que la función
uniforme f
(
z
) esté expresada bajo la forma
U
+ i
V
, donde
U, V
son funciones de s,
t.
Entonces, para cada valor de
z
corresponderá uno, y solo uno, valor para cada una de
U, V
, y, como
z
traza su camino en el plano s,
t, f
(
z
) trazará un camino correspondiente en el plano U, V: el camino de
f(z)
estará
únicamente
determinado por el de
z
. Pero si
w
es una función
multiforme
(polivalente) de
z
, tal que precisamente
n
valores diferentes de
w
estén determinados por cada valor de
z
(salvo en los puntos de ramificación donde varios valores de
w
pueden ser iguales), entonces es obvio que un plano
w
ya no basta (si
n
es mayor que 1) para representar el camino, la "marcha" de la función
w
. En el caso de una función
w
de dos valores, tal como la determinada por
w
2
=
z
se necesitan dos planos
w
y, de un modo general, para una función de
n
valores
(n
finita o infinita), hacen falta, precisamente,
n
de tales planos
w
.
Las ventajas de considerar funciones uniformes (de un valor) en lugar de funciones de n valores (n mayor que 1) aparecen de modo manifiesto, aun para quien no sea matemático. Lo que Riemann hizo fue esto: en lugar de los n planos w diferentes, introdujo una superficie de n hojas, del tipo que brevemente describiremos después, sobre la cual la función multiforme es uniforme, es decir, sobre la cual, a cada "lugar" sobre la superficie corresponde un valor, y sólo uno de las funciones representadas.
Riemann unió, por así decir, todos los planos n en un plano único y logró esto mediante un procedimiento que al principio puede parecer como una inversión de la representación de las n ramas de la función de n valores sobre n planos diferentes; pero una detenida consideración mostrará que, en efecto, restableció la uniformidad. Colocó n planos, uno sobre otro; cada uno de estos planos, u hojas, se asocia con una rama particular de la función, de modo que, en tanto que z se mueve, en una hoja particular, la correspondiente rama de la función es recorrida por w (la función de n valores de z en discusión), y como z pasa de una hoja a otra, las ramas se cambian, una en otra, hasta que, habiendo recorrido la variable z todas las hojas y habiendo vuelto a su posición inicial, la rama original se restablece. El paso de la variable z desde una hoja a otra es efectuado por medio de atajos (que pueden ser considerados como puentes rectos), que unen puntos de ramificación a lo largo de un determinado atajo que proporciona el paso de una hoja a otra se imagina un "labio" de la hoja superior pegado o unido al labio opuesto de la hoja inferior, y similarmente para el otro labio de la hoja, superior. Esquemáticamente, en sección transversal:
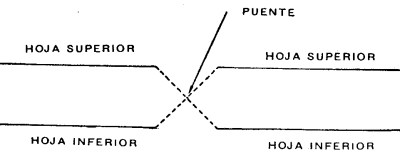
Las hojas no están unidas por atajos al azar (que pueden ser trazadas en muchas formas por determinados puntos de ramificación), sino ligadas de modo tal que, cuando z atraviesa su superficie de n hojas pasando desde una hoja a otra al alcanzar un puente o atajo, el comportamiento analítico de la función de z es descripto consecuentemente, en particular por lo que se refiere al intercambio de las ramas consiguientes sobre la variable z , si están representadas en un plano, que rodean completamente un punto de ramificación. A este circuito de un punto de ramificación del plano z único corresponde, sobre la superficie de Riemann de n hojas, el paso desde una hoja a otra y el intercambio resultante de las ramas de la función.
Existen muchas formas en que la variable puede trasladarse a la, superficie de Riemann de n hojas, pasando desde una hoja a otra. Para cada una de éstas corresponde un intercambio particular de las ramas, de la función, que puede ser simbolizado escribiendo, una tras otra, letras que denotan las diversas ramas intercambiadas. En esta forma, tenemos los símbolos de ciertas sustituciones (como en el capítulo XV) de n letras; todas estas sustituciones engendran un grupo que, en algunos aspectos, explica la naturaleza de la función considerada.
Las superficies de Riemann no son fáciles de representar gráficamente, y quienes las usan se contentan con representaciones sistemáticas de la conexión de las hojas, de una forma semejante a como los químicos escriben una fórmula "gráfica" de un complicado compuesto de carbono para representar en una forma esquemática el comportamiento químico del compuesto, pero sin que en modo alguno supongan que representa la verdadera disposición espacial de los átomos en el compuesto. Riemann hizo considerables progresos, particularmente en la teoría de funciones abelianas, por medio de sus superficies y su topología, siendo una cuestión de este tipo conseguir que los atajos sean imaginados en forma tal que hagan equivalente a un plano la superficie de n hojas. Pero los matemáticos no tienen mayor capacidad que cualquier otro mortal para imaginar complicadas relaciones espaciales, siendo excesivamente raro que posean un alto grado de "intuición" espacial.
A principios de noviembre de 1851 Riemann presentó su disertación doctoral, Grundlagen für eine allegemeine Theorie der Functionen ciner veränderlichen complexen Grösse (Fundamentos para una teoría general de las funciones de una variable compleja) a la consideración de Gauss. Esta obra del joven maestro de 25 años fue una de las pocas contribuciones modernas a la Matemática que despertó el entusiasmo de Gauss, quien cercano ya a la muerte constituía una figura casi legendaria. Cuando Riemann visitó a Gauss después de que éste había leído la disertación, el viejo maestro le comunicó que hacía años que había planeado un tratado sobre el mismo tema. El informe oficial de Gauss a la Universidad de Göttingen merece citarse como uno de los pocos casos en los que Gauss se expresó claramente.
"La disertación presentada por Herr Riemann ofrece pruebas convincentes de que ha realizado detenidas y penetrantes investigaciones en aquellas partes del tema tratadas en la disertación, de que posee una mente creadora activa, verdaderamente matemática y de que es dueño de una gloriosa y fecunda originalidad. La presentación es notable y concisa y en algunos puntos bella. La mayoría de los lectores podría preferir mayor claridad en el orden. En conjunto es una obra de valor substancial, que no sólo satisface las exigencias de las disertaciones doctorales sino que las supera".
Un mes más tarde Riemann dio su examen final, incluyendo la formalidad de una "defensa" pública de su disertación. Todo marchaba perfectamente, y Riemann comenzó a tener la esperanza de lograr una posición digna de su talento. "Creo que he mejorado mis perspectivas con mi disertación, escribía a su padre, espero también aprender a escribir más rápidamente y con mayor fluidez, especialmente si frecuento la sociedad y si tengo probabilidades de pronunciar conferencias; por tanto tengo un buen ánimo". Se excusa también ante su padre de no haber aspirado a una ayudantía vacante en el observatorio de Göttingen, pero como supone va a ser "habilitado" como Privatdozent, el porvenir no le parece demasiado negro.
Para su Habilitationsschrift Riemann pensó presentar una memoria sobre series trigonométricas (series de Fourier), pero transcurrieron dos años y medio antes de que pudiera pasar desde instructor universitario no retribuido hasta recibir las matrículas de los estudiantes por asistir a sus conferencias. Durante el otoño de 1852 Riemann aprovechó la presencia de Dirichlet en Göttingen, durante unas vacaciones, y buscó su consejo para la memoria que tenía en embrión.
Dirichlet quedó cautivo por la modestia y el talento de Riemann. "A la mañana siguiente [después de una fiesta] Dirichlet estuvo conmigo durante dos horas, escribía Riemann a su padre. Me facilitó las notas que necesitaba para mi trabajo de habilitación, que de otro modo me hubieran consumido muchas horas de estudio laborioso en la biblioteca. Leyó también mi disertación y se mostró muy amistoso, mucho más de lo que yo pudiera esperar si considero la gran distancia que existe entre nosotros. Espero que me recordará más adelante". Durante esta visita de Dirichlet realizó también excursiones con Weber y otros hombres de ciencia, y Riemann dice a su padre que estas pequeñas escapadas le hicieron científicamente mayor beneficio que si hubiera pasado las horas inclinado sobre sus libros.
Desde 1853 (Riemann tenía entonces 27 años) en adelante se dedicó intensamente a la física matemática. A finales del año había terminado su trabajo, después de muchas demoras debidas a su pasión, cada vez mayor, por la ciencia física.
Tenía aún que pasar por otro ejercicio antes de ser nombrado para el ansiado cargo. Con este objeto presentó tres temas para que la Facultad escogiese, esperando que la elección recayera sobre uno de los dos primeros, en los que estaba perfectamente preparado. Pero incautamente había incluido, como tercer tema, una cuestión en la que Gauss había trabajado sesenta años o más, los fundamentos de la Geometría, y este tema no lo había preparado. No hay duda de que Gauss sintió la curiosidad de ver como Riemann, con su gloriosamente fecunda originalidad, atacaría el difícil tema. Con gran consternación de Riemann, Gauss designó el tercer tema para que demostrara ante la Facultad su habilidad como conferenciante. "Estoy nuevamente sumido en la perplejidad, decía secretamente el imprudente joven a su padre, porque tengo que ocuparme de este tema. He reanudado mis investigaciones acerca de la relación entre electricidad, magnetismo, luz y gravitación, y he progresado tanto que puedo publicar este estudio sin temor. Estoy cada vez más convencido de que Gauss ha trabajado en este tema durante años, y ha hablado acerca de él con algunos amigos,(Weber entre otros). Secretamente os escribo, pues no quiero parecer arrogante, pero espero que aun no sea demasiado tarde para mí y que obtendré el reconocimiento como investigador".
El esfuerzo de realizar dos investigaciones extraordinariamente difíciles simultáneamente, mientras actuaba como ayudante de Weber en el seminario de física matemática, unido a los obstáculos de la pobreza produjeron en él un derrumbe temporal. "He estado tan absorbido en mi investigación sobre la unidad de todas las leyes físicas, que cuando me fue entregado el tema para mi conferencia, no pude abandonar la investigación. Luego, en parte como resultado de las meditaciones, en parte debido a mi permanencia constante en lugares cerrados durante esta mala estación, caí enfermo; mis viejos males se repitieron con gran frecuencia, y no pude continuar mi labor. Varias semanas más tarde, al mejorar el tiempo, comencé a sentirme mejor. Para el verano alquilé una casa con un jardín, y desde entonces mi salud no se ha alterado. Habiendo terminado dos semanas después de Pascua una parte de mi trabajo, comencé a dedicarme a mi conferencia y la terminé alrededor de Pentecostés [es decir en siete semanas]. Tuve alguna dificultad para fijar la fecha de mi conferencia, y hasta creí que tendría que volver a Quickborn sin haber logrado mi objeto. Gauss está gravemente enfermo, y los médicos creen que su muerte es inminente. Estando demasiado débil para asistir a mis pruebas, me pidió que esperase hasta agosto, creyendo que mejoraría su salud. Luego, el viernes después de Pentecostés, decidió que la conferencia tuviera lugar al día siguiente a las 11,30. El sábado me sentía feliz con estos acontecimientos".
Este es el relato de Riemann respecto a su conferencia histórica, que habría de revolucionar la Geometría diferencial, y preparar el camino para la física geometrizada de nuestra generación. En la misma carta narra cómo realizó su labor durante la Pascua. Weber y algunos de sus colaboradores "han hecho mediciones muy exactas de un fenómeno que hasta entonces no había sido investigado, la carga residual en una botella de Leyden [después de la descarga se observa que la botella no ha quedado completamente descargada]. Le comuniqué [a uno de los colaboradores de Weber, Kohlrauch] mi teoría de este fenómeno, que he elaborado especialmente para este fin. He encontrado su explicación mediante mis investigaciones acerca de la relación entre electricidad, luz y magnetismo. Esta cuestión era muy importante para mí, pues es la primera vez que he podido aplicar mi trabajo a un fenómeno aun desconocido, y espero que la publicación contribuirá a que mi obra más amplia sea recibida favorablemente".
La conferencia de prueba de Riemann (10 de junio de 1854) fue acogida tan cordial como podía desear su carácter modesto. La preparación de su conferencia le hizo sudar sangre, pues estaba decidido a hacerla inteligible hasta para aquellos miembros de la Facultad que tuvieran escaso conocimiento de Matemática. Aparte de constituir una de las grandes obras maestras de la Matemática, el ensayo de Riemann Ueber die Hypothesen welche der Geometrie zu Grunde liegen. (Sobre las hipótesis que sirven de fundamento a la geometría) es también perfecta en su presentación. Gauss estaba entusiasmado. "Contra la tradición eligió el tercero de los tres temas presentados por el candidato deseando ver como esa difícil cuestión era tratada por un hombre tan joven. Su sorpresa fue más allá de todas sus esperanzas, y al volver de la reunión de la Facultad manifestó a Wilhelm Weber su más alta estima por las ideas presentadas por Riemann, hablando con un entusiasmo que era raro en Gauss". Lo poco que puede decirse en este lugar acerca de esta obra maestra será reservado para la conclusión de este capítulo.
Después de una temporada de reposo en Quickborn, en compañía de su familia, Riemann volvió en septiembre a Göttingen, donde preparó apresuradamente una conferencia (dedicando a este trabajo las noches para poder tenerla terminada), que debía ser pronunciada en una reunión de hombres de ciencia. Su tema era la propagación de la electricidad en los no conductores. Durante el año continuó sus investigaciones en la teoría matemática de la electricidad, y preparó un trabajo sobre los anillos coloreados de Nobili. Refiriéndose a este estudio escribía a su hermana Ida: "Este tema es importante, porque se pueden hacer mediciones muy exactas en relación con él, y comprobar las leyes de acuerdo a las cuales la electricidad se mueve".
En la misma carta (9 de octubre de 1854) expresa su ilimitado goce por el triunfo de su primera conferencia académica, y su gran satisfacción por el inesperado gran número de oyentes. ¡Habían venido a oírle ocho estudiantes! Riemann suponía que no llegarían a dos o tres. Alentado por esta inesperada popularidad Riemann escribía a su padre: "He sido capaz de mantener regularmente mis clases. Mi primera desconfianza ha ido disminuyendo cada vez más, y me he habituado a pensar más en los oyentes que en mí mismo y a leer en sus expresiones si debo pasar a otros puntos o explicar más detenidamente la cuestión".
Cuando Dirichlet sucedió a Gauss en 1855, los amigos de Riemann solicitaron de las autoridades universitarias el nombramiento de éste como profesor ayudante, pero las finanzas de la Universidad no eran muy abundantes. De todos modos, le fue concedido un sueldo equivalente a doscientos dólares por año, preferible a la inseguridad de las matrículas de media docena de estudiantes voluntarios. Su futuro le apesadumbraba, y cuando perdió a su padre y a su hermana Clara, no siéndole ya posible trasladarse a Quickborn durante las vacaciones Riemann se entristeció profundamente. Sus tres restantes hermanas fueron a vivir con el otro hermano, que era empleado de correos de Bremen, cuyo sueldo era principesco al lado de la posición económica del matemático.
Al siguiente año (1856; Riemann tenía entonces 30 años), las perspectivas se aclararon un poco. Era imposible el desaliento para un genio creador como Riemann, en tanto pudiera disponer de los exiguos medios para seguir viviendo. A este período pertenece parte de su obra característicamente original sobre las funciones abelianas, sus trabajos clásicos sobre las series hipergeométricas (véase el capítulo sobre Gauss) y las ecuaciones diferenciales, de gran importancia en la física matemática, sugeridas por estas series. En esas obras Riemann señala nuevas direcciones. Su capacidad de generalización, su notable intuición en la forma de abordar los problemas, constituían características de este autor. Sus trabajos absorbieron todas sus energías e hicieron felices sus horas, a pesar de las tristezas materiales; posiblemente este fatal optimismo era propio de la tuberculosis que ya se indicaba.
Las investigaciones de Riemann en la teoría de funciones abelianas difiere tanto de los estudios de Weierstrass como la luz de la Luna difiere de la luz del Sol. La manera como abordaba los problemas Weierstrass era metódica, exacta en todos sus detalles, como el avance de un ejército perfectamente disciplinado bajo el mando de un general que prevé todas las contingencias. Riemann, en cambio, abarcaba todo el campo, sin cuidarse de los detalles, contentándose con reconocer las posiciones clave en la topografía general. El método de Weierstrass era aritmético, el de Riemann geométrico e intuitivo. Decir que uno es mejor que otro carece de sentido, pues ambos no pueden ser examinados desde un punto de vista común.
El exceso de trabajo y la falta de comodidades provocó en Riemann un derrumbe nervioso cuando tenía 30 años, y el joven se vio forzado a trasladarse durante algunas semanas, con un amigo, a la región montañosa de Hartz, donde fue visitado por Dedekind. Los tres realizaron largos viajes por las montañas, y Riemann se restableció pronto. Librado del esfuerzo de los deberes académicos, Riemann entretenía a sus compañeros con su excelente humor. Entre ellos hablaban de sus problemas, como acostumbran a hacerlo, cuando se reúnen, los juristas, los médicos o los hombres de negocios. Una tarde, después de una fatigosa caminata, Riemann aludió a la vida de Newton, de Brewster, hablando de la carta de Bentley, en la cual Newton mismo afirma la imposibilidad de la acción a distancia sin la intervención de un medio. Esta afirmación produjo el entusiasmo de Riemann, inspirándole una espontánea conferencia. En la actualidad, el "medio" que Riemann defendía no es el éter luminífero, sino su propio "espacio curvado", o su reflexión en el espacio-tiempo de la relatividad.
Al fin, en 1857, teniendo 31 años, Riemann obtuvo el cargo de profesor ayudante. Su sueldo era el equivalente a 300 dólares por año, pero como no estaba habituado a la riqueza, le bastaba. Pero entonces se produjo un verdadero desastre: su hermano murió, y desde entonces tuvo que cuidar de sus tres hermanas. Tocaban exactamente a 75 dólares al año por cabeza. No hay, pues, que sorprenderse de que contrajera una tuberculosis. Sin embargo, el Señor que tan generosamente se mostró, pronto alivió a Riemann de la carga de su hermana menor, Marie, de modo que el ingreso individual podía calcularse en 100 dólares por año y persona. Si las raciones tenían que ser escasas, el cariño era abundante, y Riemann se veía más que pagado de sus sacrificios por la devoción de sus hermanas, que le alentaban en su trabajo. El Señor parece haber sabido que si algún mortal necesita aliento, el pobre Riemann no era el que menos lo necesitaba.
En 1858 Riemann escribió su trabajo sobre electrodinámica, del cual comunica a su hermana Ida el siguiente comentario: "Mi descubrimiento relacionado con la íntima conexión entre electricidad y luz lo he dedicado a la Real Sociedad [de Göttingen]. Por lo que he oído, Gauss ideó otra teoría, respecto a esta íntima relación, diferente de la mía, y la comunicó a sus íntimos amigos. Sin embargo, estoy plenamente convencido de que mi teoría es la exacta, y que en pocos años será reconocida como tal." Como es sabido Gauss pronto retiró su memoria y no la publicó; probablemente no estaba satisfecho de ella. Parece que Riemann fue demasiado optimista; pues es la teoría electromagnética de Clerk Maxwell la que hoy se admite, en los fenómenos macroscópicos. El presente estado de las teorías de la luz y del campo electromagnético es demasiado complicado para ser descripto en este lugar; bastará añadir que la teoría de Riemann fue desechada.
Dirichlet murió el 5 de mayo de 1859. Siempre apreció a Riemann e hizo cuanto pudo para ayudar al joven en sus luchas. El interés de Dirichlet, que había aumentado rápidamente la reputación de Riemann fue la causa de que el gobierno nombrase a éste como sucesor. En consecuencia, a los 33 años Riemann fue el segundo sucesor de Gauss. Para aliviar sus dificultades económicas, las autoridades universitarias le permitieron residir en el Observatorio, como Gauss había hecho. El reconocimiento sincero, el elogio de los matemáticos, que aunque más viejos que él eran en cierto grado sus rivales, no se hizo esperar. En una visita a Berlín fue felicitado por Borchartd, Kummer, Kronecker, y Weierstrass. Las Sociedades doctas, incluyendo la Sociedad Real de Londres y la Academia Francesa de Ciencias, le honraron nombrándole miembro, y en poco tiempo obtuvo todas las distinciones que puede recibir un hombre de ciencia. Una visita a París, en 1860 le permitió conocer a los principales matemáticos franceses, particularmente a Hermite, cuya admiración por Riemann era ilimitada. Dicho año es memorable en la historia de la física matemática, por ser aquel el que Riemann comenzó a trabajar intensamente sobre su memoria Uber eine Frage der Wärmeleitung. (Sobre una cuestión de la conducción del calor), en la que desarrolla toda la cuestión de las formas diferenciales cuadráticas (que será mencionada en relación con la ,obra de Riemann sobre los fundamentos de la Geometría), que es básica en la teoría de la relatividad.
Sus problemas materiales habían mejorado considerablemente con su nombramiento de profesor titular, y Riemann pudo casarse cuando tenía 36 años. Su mujer, Elise Koch, era amiga de sus hermanas. Un mes después de su matrimonio Riemann cayó enfermo (julio de 1862), con pleuresía. Una curación incompleta dio lugar a la tuberculosis. Amigos influyentes pidieron al gobierno que concediera a Riemann los fondos necesarios para que convaleciera en el suave clima de Italia, donde permaneció aquel invierno. La primavera siguiente, en su viaje de regreso a Alemania, pudo visitar los tesoros de arte de muchas ciudades italianas. Este fue el breve verano de su vida.
Lleno de esperanza dejó su amada Italia, pero volvió a caer gravemente enfermo al llegar a Göttingen. En el viaje de regreso se había cuidado muy poco, y durante un paseo por la nieve sufrió un grave enfriamiento. El siguiente agosto (1863) volvió a Italia, deteniéndose primero en Pisa donde nació su hija Ida, (llamada así en recuerdo de su hermana mayor). El invierno fue excepcionalmente crudo y el río Arno se congeló. En mayo se trasladó a una pequeña villa en los suburbios de Pisa. Allí murió su hermana menor Helene, y su enfermedad, complicada con ictericia, se hizo cada vez más grave. Con gran pesar se vio obligado a rechazar la cátedra que le ofreció la Universidad de Pisa. La Universidad de Göttingen le concedió generosamente permiso para permitirle pasar el invierno en Pisa rodeado por sus amigos, los matemáticos italianos. Pero nuevas complicaciones le hicieron volver al hogar, y después de haber buscado vagamente la salud en Liorna y Génova, regresó en octubre a Göttingen, donde pasó un invierno tolerable.
Durante toda esta época trabajó cuanto pudo. En Göttingen expresó muchas veces el deseo de hablar con Dedekind de las obras que no había completado, pero jamás se sintió lo suficientemente fuerte para realizar la visita. Uno de sus últimos proyectos fue trabajar sobre la mecánica del oído, estudio que dejó incompleto. Esperaba terminar este trabajo, así como algunos otros, que consideraba de gran importancia, y en un final intento de recobrar su vigor volvió a Italia.
Sus últimos días pasaron en una villa, en Selasca, a orillas del Lago Mayor.
Dedekind cuenta cómo murió su amigo: "Sus fuerzas declinaban rápidamente, y sentía que su fin estaba próximo. El día antes de su muerte trabajaba bajo una higuera, el alma henchida de gozo en el glorioso paisaje que se extendía alrededor de él... Su vida se deslizaba suavemente sin lucha ni agonía. El enfermo parecía seguir con interés la separación del alma y del cuerpo; su mujer le daba pan y vino... él le decía. Besa a nuestra hija. Ella repetía el Padrenuestro, que el moribundo era incapaz de repetir; en las palabras 'Perdónanos nuestras deudas', él la miró cariñosamente; la mujer sintió su mano cada vez más fría entre las de ella, y después de algunos suspiros, su puro y noble corazón dejó de latir. La suave mente forjada en la casa de su padre, permaneció durante toda su vida, y sirvió a su Dios con tanta fidelidad como su padre había hecho, pero de modo diferente".
Riemann murió en plena gloria de su genio maduro, el 20 de julio de 1866, teniendo 39 años. La inscripción sobre su lápida costeada por sus amigos italianos, termina con las palabras "Denen die Gott lieben müssen alle Dinge zum Besten dienen" (Aquellos que aman a Dios deben servirse de todas las cosas del mejor modo).
La grandeza de Riemann como matemático reside en su poderosa capacidad de generalización y en el alcance ilimitado de los métodos y nuevos puntos de vista que descubrió tanto en la Matemática pura como en la Matemática aplicada. Los detalles jamás le importaron, y apreciaba el conjunto de un vasto problema en la forma de una unidad coherente. Hasta en las notas fragmentarias; en los proyectos incompletos, muestra la novedad, y nos permite pensar que Riemann murió mucho antes de haber realizado toda su labor. En este lugar tan sólo podemos hablar de una de sus grandes obras maestras, la memoria de 1854 sobre los fundamentos de la Geometría, y aunque no pudo ser fácil a Clifford utilizarla simplemente para proponer otra Geometría, citaremos su audaz trabajo de 1870 (On the space - theorie of matter) sobre la teoría-espacio de la materia como una introducción singularmente profética al cuerpo y al espíritu de la Geometría de Riemann.
Clifford no era un plagiario servil, sino un hombre con un talento brillantemente original, del cual podía decirse, como Newton dijo de Cotes: "De haber vivido, podríamos haber conocido alguna cosa". El lector que esté familiarizado con algunas de las mejores vulgarizaciones de la física relativista y de la teoría ondulatoria de los electrones reconocerá varias curiosas anticipaciones de las teorías corrientes en la breve profecía de Clifford.
"Riemann ha demostrado que existen diferentes tipos de líneas y superficies, de modo que existen tipos diferentes de espacio de tres dimensiones; y sólo por la experiencia podemos descubrir a cuál de estos tipos pertenece el espacio en que vivimos. En particular, los axiomas de la geometría plana son exactos dentro de los límites del experimento sobre la superficie de una hoja de papel, y sin embargo, sabemos que la hoja está realmente cubierta de cierto número de pequeñas arrugas y surcos, sobre los cuales (no siendo cero la curvatura total) estos axiomas no son verdaderos. Análogamente, dice dicho autor, aunque los axiomas de la Geometría del espacio son verdaderos dentro de los límites del experimento para porciones finitas de nuestro espacio, no hay razón para concluir que son ciertos para porciones muy pequeñas, y si una ayuda puede ser obtenida de este modo para la explicación de los fenómenos físicos, podemos tener razones para concluir que no son ciertos para porciones muy pequeñas del espacio.
"Deseo aquí indicar una forma en que estas especulaciones pueden ser aplicadas a la investigación de los fenómenos físicos. Mantengo, en efecto:
- Que pequeñas porciones del espacio son de hecho de una naturaleza análoga a pequeñas colinas en una superficie que está sobre la llanura, o sea que las leyes ordinarias de geometría no son válidas en ellas.
- Que esta propiedad de estar curvada o deformada pasa continuamente desde una porción del espacio a otra a la manera de una onda.
- Que esta variación de la curvatura del espacio es lo que realmente tiene lugar en ese fenómeno que llamamos el movimiento de la materia, sea ponderable o etérea.
- Que en el mundo físico no tiene lugar otra cosa que esta variación, sujeta (posiblemente) a la ley de continuidad.
Riemann creyó también que su nueva Geometría sería de importancia científica, según lo muestra la conclusión de su memoria.
"Por tanto la realidad que yace bajo el espacio debe formar una variedad discontinua, o debemos buscar el fundamento de sus relaciones métricas fuera de él, en fuerzas de unión que sobre él actúan.
"La respuesta a estas cuestiones tan sólo pueden ser logradas partiendo de la concepción de fenómenos que hasta ahora han sido comprobados por la experiencia, y que Newton acepta como un fundamento, y haciendo en esta concepción los cambios sucesivos requeridos por los hechos que no puede explicar". Luego sigue diciendo que investigaciones como las suyas, que parten de nociones generales, "pueden ser útiles para impedir que este trabajo se vea obstaculizado por conceptos demasiado estrechos, y que el progreso del conocimiento de la interdependencia de las cosas sea frenado por prejuicios tradicionales.
"Esto nos lleva al dominio de otra ciencia, el de la física, en la que el objeto de este trabajo no nos permite penetrar hoy".
La obra de Riemann de 1854 iluminó la Geometría con una nueva luz. La Geometría que él imagina es no euclidiana, no en el sentido de Lobatchewsky y Johann Bolyai, ni tampoco en el de la elaboración de Riemann de la hipótesis del ángulo obtuso (explicada en el capítulo XVI), sino en un sentido más comprensivo, dependiente del concepto de medida. Considerar las relaciones de medida como el nervio de la teoría de Riemann es cometer una injusticia. La teoría contiene mucho más que una aprovechable filosofía de la medida; pero ésta es una de sus principales características. Ningún párrafo de la concisa memoria de Riemann sintetiza lo que hay en ella; de todos modos intentaremos describir algunas de sus ideas básicas, y elegiremos tres: el concepto de multiplicidad, la definición de distancia y la noción de curvatura de una multiplicidad.
Una multiplicidad es una clase de objetos (al menos en la Matemática común) tal que cualquier miembro de la clase puede ser completamente especificado asignándole ciertos números, en un orden definido, que corresponden a propiedades "numerables" de los elementos, correspondiendo la asignación en el orden dado a un orden preasignado de las propiedades "numerables". Aunque se conceda que esto pueda ser hasta menos comprensible que la definición de Riemann, es, de todos modos, una base de trabajo desde la cual partir, y a todo lo que se llega en la Matemática es a esto: una multiplicidad es una serie de n-ples " ordenada de números ( x 1 , x 2 , …, x n ) donde los paréntesis, indican que los números x 1 , x 2 , …, x n se han de escribir en el orden dado. Dos de tales n-ples, ( x 1 , x 2 , …, x n ) y ( y 1 , y 2 , …, y n ) son iguales cuando, y sólo cuando los números correspondientes en ellos son respectivamente iguales, o sea cuando, y sólo cuando, x 1 = y 1 , x 2 = y 2, … , x n = y n .
Si precisamente n números se presentan en cada uno de estos n-ples en la multiplicidad, se dice que la multiplicidad será de n dimensiones. Así tenemos que volver a las coordenadas de Descartes. Si cada uno de los números ( x 1 , x 2 , …, x n ) es un entero positivo, cero o negativo, o si es un elemento de cualquier serie numerable (una serie cuyos elementos pueden ser contados 1, 2, 3 ... ), y si lo mismo ocurre para cualquier n-ple en la serie, se dice que la multiplicidad es discontinua. Si los números x 1 , x 2 , …, x n , pueden tomar valores continuamente (como en el movimiento de un punto a lo largo de una línea) la multiplicidad es continua.
Esta definición ha pasado por alto deliberadamente, la cuestión de si la serie de n-ples ordenada es "la multiplicidad", o si alguna cosa "representada por" esta es "la multiplicidad". Así, cuando decimos que ( x,y ) son las coordenadas de un punto en un plano, no preguntamos lo que es "un punto en un plano", sino que procedemos a actuar con estas parejas ordenadas de números x,y ), donde x,y toman todos los valores reales independientemente. En cambio, puede algunas veces ser ventajoso fijar nuestra atención sobre lo que representa un símbolo como ( x,y ). Por ejemplo, si x es la edad en segundos de un hombre e y su altura en centímetros, podemos estar interesados en el hombre (o la clase de todos los hombres), más bien que en sus coordenadas, con las cuales está relacionada tan sólo la Matemática de nuestra pesquisa. En este mismo orden de ideas, la Geometría ya no se refiere a lo que el "espacio" "es", si "es" significa o no algo en relación al "espacio". El espacio, para un matemático moderno, es simplemente una multiplicidad, número del tipo antes descripto, y esta concepción del espacio se deriva de las "multiplicidades" de Riemann.
Pasando a la medida, Riemann afirma que "la medida consiste en una superposición de las magnitudes que han de ser comparadas. Si esto falta, las magnitudes pueden ser comparadas tan sólo cuando una es parte de otra, y entonces sólo se puede decidir acerca del más o el menos, pero no del cuánto". Puede decirse de pasada que una teoría consecuente y útil de la medida es actualmente un deseo urgente en la física teórica, particularmente en todas las cuestiones donde son de importancia los cuantos y la relatividad.
Descendiendo una vez más desde las generalidades filosóficas a la, Matemática menos mística, Riemann procedió a establecer una definición de distancia, basada en su concepto de medida, que ha sido extraordinariamente fructífera en física y en matemática.
El teorema pitagórico
o
donde a es la longitud de la diagonal de un rectángulo y b , c las longitudes de los dos lados, es la fórmula fundamental para la medida de distancias en un plano. ¿Cómo extenderemos esta fórmula a una superficie curva?
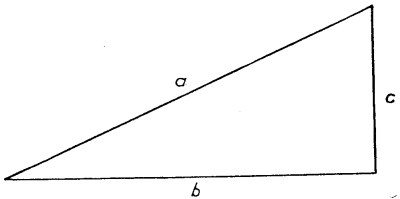
A las líneas rectas del plano corresponden geodésicas (véase capítulo XIV) de la superficie; pero en una esfera, por ejemplo la proposición pitagórica no es cierta para un triángulo rectángulo formado por geodésicas. Riemann generalizó el teorema de Pitágoras para cualquier multiplicidad del siguiente modo:
Supongamos que
son las coordenadas de dos "puntos" de la multiplicidad que están "infinitamente próximos" uno de otro. Para nuestro propósito la significación de "infinitamente próximo" es que las potencias superiores a la segunda de x' 1 , x' 2 , …, x' n , que miden la separación de los dos puntos en la multiplicidad, se pueden despreciar. Por sencillez estableceremos la definición cuando n = 4 que da la distancia entre dos puntos próximos en un espacio de cuatro dimensiones: la distancia es la raíz cuadrada de
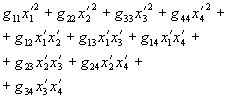
en las que los 10 coeficientes g 11 ,…, g 34 son funciones de x 1 , x 2 , x 3 , x 4 . Para valores particulares de las g , se define un "espacio". Así, podemos tener
g 22 = 1,
g 33 = 1,
g 44 = 1
y todas las restantes g cero; o podemos considerar un espacio en el cual todas las g, salvo 944 Y 934 fueran cero, y así sucesivamente. Un espacio considerado en relatividad es de este tipo general, en el que todas las g salvo g 44 y g 34 son cero, y existen ciertas expresiones simples que abarcan x 1 , x 2 , x 3 , x n .
En el caso de un espacio n-dimensional la distancia entre puntos próximos se define en una forma similar; la expresión general contiene
Una vez dada la fórmula pitagórica generalizada para la distancia entre puntos próximos es un problema de Cálcalo integral encontrar la distancia entre dos puntos cualesquiera del espacio. Un espacio cuya métrica (sistema de medida) se define por una fórmula del tipo descripto se llama riemanniano.
La curvatura, según la concibe Riemann (y antes de él Gauss; véase capítulo sobre este último), es otra generalización de la experiencia común. Una línea recta tiene curvatura cero; la "medida" de la cantidad en que una línea curva se separa de la recta puede ser la misma para cualquier punto de la curva, como ocurre para un círculo), o puede variar de un punto a otro de la curva, cuando se hace necesario además expresar la "cantidad de curvatura" empleando infinitésimos. Para las superficies curvas, la curvatura se mide similarmente por la desviación de un plano que tiene curvatura cero. Esto puede ser generalizado y precisado algo más del siguiente modo. Por simplicidad planteamos primero la situación para un espacio bidimensional, o sea para una superficie como nosotros imaginamos ordinariamente las superficies. Es posible partiendo de la fórmula
que expresa (como antes) el cuadrado de la distancia entre puntos próximos sobre una superficie dada (determinada cuando las funciones g 11 , g 12 , g 22 son dadas), calcular la medida de la curvatura de cualquier punto de la superficie completamente en función de g 11 , g 12 , g 22 . Ahora bien, en el lenguaje ordinario, hablar de la curvatura de un espacio de más de dos dimensiones es decir algo sin significación. De todos modos, Riemann, generalizando los conceptos de Gauss, procedió en la misma forma matemática para construir una expresión que comprende todas las g en el caso general de un espacio n-dimensional, que es matemáticamente del mismo tipo que la expresión gaussiana para la curvatura de una superficie, y esta expresión generalizada es lo que llamó la medida de la curvatura del espacio. Es posible mostrar representaciones visuales de un espacio curvo de más de dos dimensiones, pero tales ayudas a la perfección son tan útiles como puedan ser un par de muletas rotas para un hombre que no tenga piernas, pues no añade nada a la comprensión y son matemáticamente inútiles.
¿Por qué realizó Riemann toda esta labor y qué beneficios ha reportado? No intentaremos responder a lo primero, salvo decir que Riemann hizo lo que hizo porque su demonio le impulsó. Y brevemente enumeraremos algunas de las ventajas que se han obtenido de la revolución llevada a cabo por Riemann en el pensamiento geométrico. En primer término llevó la creación de "espacios" y "geometrías" en número ilimitado para fines específicos, uso en la dinámica o en la geometría pura, o en la ciencia física, dentro de las capacidades de los geómetras profesionales, y reunió enorme número de teoremas geométricamente importantes formando grupos compactos, que pueden ser tratados más fácilmente en su conjunto. En segundo término aclaró nuestro concepto del espacio, al menos en tanto que los matemáticos se ocupen del "espacio", y despojó a esa nulidad mística llamada espacio de su última sombra de misterio. Las enseñanzas de Riemann han mostrado a los matemáticos a desconfiar de cualquier Geometría o de cualquier espacio como una forma necesaria de percepción humana. Fue el último clavo en el ataúd del espacio absoluto y el primero en el de los "absolutos" de la física del siglo XIX.
Finalmente, la curvatura que Riemann definió, los procesos que ideó para la investigación de las formas diferenciales cuadráticas (las que dan la fórmula para el cuadrado de la distancia entre puntos próximos de un espacio de cualquier número de dimensiones), y su reconocimiento de que la curvatura es un invariante (en el sentido técnico explicado en los capítulos anteriores), encuentran sus interpretaciones físicas en la teoría de la relatividad. Si ésta ha llenado o no su fórmula final es otra cuestión; desde la relatividad, nuestro concepto de la ciencia física no es el que era antes. Sin la obra de Riemann esta revolución en el pensamiento científico hubiera sido imposible, a no ser que algún hombre hubiera creado posteriormente los conceptos y los métodos matemáticos que Riemann creó.
|
|
|