LOBATCHEWSKY

La teoría de Lobatchewsky era incomprensible para sus contemporáneos, pues parecía contradecir un axioma cuya necesidad está basada tan sólo sobre un prejuicio santificado por millares de años. Los editores de las obras de Lobatchewsky

Suponiendo que sea exacta la opinión comúnmente aceptada de la importancia de la obra de Copérnico, hay que admitir que el más alto galardón o la más grave condenación humana posible es llamar a otro hombre el "Copérnico" de alguna cosa. Cuando consideremos lo que Lobatchewsky hizo al crear la Geometría no-euclidiana y comprendamos su significación para todo el pensamiento humano del cual la Matemática es sólo una parte pequeña, aunque muy importante, probablemente aceptaremos que Clifford (1845-1879), que era un gran geómetra y bastante más que un simple matemático, no exageró al calificar a Lobatchewsky como "el Copérnico de la geometría".

Nikolas Ivanovitch Lobatchewsky, segundo hijo de un modesto funcionario del gobierno, nació el 2 de noviembre de 1793 en el distrito de Makarief, gobernación de Nijni Novgorod, Rusia. El padre murió cuando Nikolas tenía siete años, dejando a su mujer, Praskovia Ivanovna, el cuidado de sus tres hijos pequeños. Como el sueldo del padre mientras vivió apenas bastaba para mantener a su familia, la viuda quedó en extrema pobreza. Se trasladó a Kazan, donde preparó lo mejor que pudo a sus hijos para ingresar en la escuela, y tuvo la satisfacción de ver cómo uno tras otro ingresaron en el Instituto. Nikolas fue admitido en 1802, teniendo 8 años. Sus progresos fueron enormemente rápidos tanto en la matemática como en los clásicos. A los 14 años estaba preparado para ingresar en la Universidad. En 1807 ingresó en la Universidad de Kazan, fundada en 1805, en donde transcurrieron los siguientes 40 años de su vida como estudiante, profesor ayudante, profesor y finalmente Rector. Deseando elevar la Universidad de Kazan al nivel de las de Europa, las autoridades universitarias habían traído de Alemania distinguidos profesores. Entre éstos se hallaba el astrónomo Littrow, que más tarde fue director del observatorio de Viena. Los profesores alemanes rápidamente reconocieron el genio de Lobatchewsky y le alentaron.

En 1811, teniendo 18 años, Lobatchewsky obtuvo su título después de una breve reyerta con las autoridades universitarias en cuya ira había incurrido por su exuberancia juvenil. Los amigos alemanes de la Facultad le defendieron y obtuvo su título. Por esta época su hermano mayor Alexis estaba encargado de los cursos elementales de Matemática para los funcionarios secundarios del gobierno, y cuando Alexis tomó licencia por enfermedad, Nikolas fue su sustituto. Dos años más tarde, teniendo 21 años, Lobatchewsky fue nombrado "profesor extraordinario", equivalente al profesor asistente de otras Universidades.

El nombramiento de Lobatchewsky como profesor ordinario tuvo lugar en 1816, a la precoz edad de 23 años. Sus deberes eran pesados. Además del curso de Matemática fue encargado de los cursos de astronomía y de física, el primero para sustituir a un colega que disfrutaba de licencia. El extraordinario equilibrio con que realizó su pesada labor hizo de él un candidato para que se le encargaran nuevos trabajos, basándose en la teoría de que un hombre capaz de hacer muchas cosas es capaz de hacer todavía más, y por entonces Lobatchewsky fue nombrado bibliotecario de la Universidad y conservador del Museo de la Universidad donde reinaba un desorden caótico.

Los estudiantes suelen ser una masa ingobernable antes de que la vida les enseñe que no se trata simplemente de ganar lo necesario para vivir. Entre los innumerables deberes de Lobatchewsky, desde 1819 hasta la muerte del zar Alejandro en 1825, se contaba el de ser Inspector de todos los estudiantes de Kazan, desde los asistentes de las escuelas elementales hasta los hombres ya hechos que seguían cursos para postgraduados en la Universidad. Esta inspección se refería especialmente a las opiniones políticas de los estudiantes. Podemos imaginar lo ingrato de tal tarea. La habilidad con que Lobatchewsky supo desenvolver para enviar sus informes día tras día y año tras año a sus suspicaces superiores sin ser tachado de benevolencia para el espionaje, y sin perder el sincero respeto y el cariño de los estudiantes, dice más de su capacidad administrativa que todos los honores y medallas que pudiera conferirle el gobierno, y con las que él gustaba adornarse en las ocasiones oportunas.

Las colecciones del Museo de la Universidad constituían un increíble revoltijo. Un desorden análogo hacía prácticamente inutilizable la abundante biblioteca. Lobatchewsky fue encargado de poner orden. Como reconocimiento a sus señalados servicios las autoridades le elevaron al cargo de Decano de la Facultad de Matemática y Física, pero como se olvidaron de votar los fondos necesarios para ordenar la biblioteca y el museo, Lobatchewsky hizo este trabajo con sus propias manos, catalogando, limpiando el polvo, cuidando de las vitrinas, y hasta si era necesario barriendo.

Con la muerte de Alejandro, en 1825, las cosas parecieron mejorar. El funcionario responsable de la maliciosa persecución de la Universidad de Kazan fue eliminado al ser considerado como demasiado corrompido para desempeñar un cargo del gobierno, y su sucesor nombró un conservador profesional para aliviar a Lobatchewsky de sus infinitas tareas de catalogar libros, limpiar el polvo a las muestras de numerales y atacar la polilla de los pájaros disecados. Necesitando apoyo moral y político para su obra en la Universidad, el nuevo conservador influyó para que fuera nombrado Rector Lobatchewsky, cosa que se logró el año 1827. El matemático se hallaba ahora a la cabeza de la Universidad, pero la nueva posición no era una sinecura. Bajo su capaz dirección todo el cuerpo docente fue reorganizado, siendo nombrados nuevos y mejores hombres. La instrucción fue liberalizada, a pesar de la función oficial, la biblioteca adquirió un nivel superior de suficiencia científica, se adquirieron los instrumentos científicos requeridos para la investigación y la enseñanza, se fundó y equipó un observatorio, proyecto acariciado por el enérgico Rector, y la amplia colección mineralógica donde estaban representados todos los minerales de Rusia, fue puesta en orden y constantemente enriquecida.

La nueva dignidad de su rectorado no impidió que Lobatchewsky ayudara manualmente en los trabajos de la biblioteca y del museo cuando era necesario. La Universidad era su vida y la amaba sobre todas las cosas. Poco bastaba para que despojándose del cuello y de la levita se entregara a cualquier labor manual. Se cuenta que un distinguido visitante extranjero, al encontrar al Rector en mangas de camisa, le confundió con un conserje y le pidió le mostrara la biblioteca y las colecciones del museo. Lobatchewsky le mostró los más preciados tesoro añadiendo detenidas explicaciones. El visitante quedó encantado muy impresionado de la gran inteligencia y cortesía de los empleados subalternos rusos. Al despedirse quiso entregarle una pequeña propina pero Lobatchewsky, ante la admiración del extranjero, rechazó indignado las monedas ofrecidas. Pensando que se trataba de alguna excentricidad del inteligente conserje, el visitante se guardó su dinero. Aquella noche, él y Lobatchewsky volvieron a encontrarse en la cena ofrecida por el gobernador, y en ese momento se presentaron y aceptaron recíprocamente todo género de excusas.

Lobatchewsky creía firmemente en que para hacer bien una cosa hay que saber ejecutarla o comprender como se ejecuta, pues es la única manera de poder criticar el trabajo de los demás de un modo inteligente y constructivo. Como hemos dicho, la Universidad era su vida. Cuando el gobierno decidió modernizar los edificios y añadir un nuevo, Lobatchewsky tomó a su cuidado que la obra fuera realizada del modo más perfecto sin que se derrochasen los fondos votados. Para cumplir esta tarea aprendió arquitectura. Tan grande fue su dominio de la cuestión que los edificios no sólo fueron adecuados para el propósito a que se destinaban, sino que se dio el caso, casi único en la historia, de que fueron construidos con menos dinero que el calculado. Algunos años más tarde (en 1842), un terrible fuego destruyó la mita de la ciudad de Kazan, incluyendo los mejores edificios de la Universidad con su observatorio totalmente equipado, que constituía el orgullo de Lobatchewsky. Pero gracias a la enérgica sangre fría del Rector se salvaron los instrumentos y la biblioteca. Apagado el fuego, Lobatchewsky se entregó a la labor de la reconstrucción, y dos años más tarde no quedaba signo alguno del desastre.

Recordaremos que el año 1842, el año del fuego, fue también el año en que, merced a los buenos oficios de Gauss, fue elegido Lobatchewsky miembro extranjero correspondiente de la Real Sociedad de Göttingen por su creación de la Geometría no-euclidiana. Aunque parezca increíble que un hombre tan excesivamente atareado por la enseñanza y la administración como Lobatchewsky lo estaba, pudiera encontrar tiempo para realizar una obra científica, Lobatchewsky encontró la oportunidad para crear una de las grandes obras maestras de la Matemática y para establecer un jalón en el pensamiento humano. En esa obra trabajó durante 20 o más años. Su primera comunicación pública acerca de ese tema ante la Sociedad Físico-matemática de Kazan, tuvo lugar en 1826. Fue igual que si hubiera hablado en pleno desierto de Sahara. Gauss no oyó hablar de la obra basta el año 1840.

Otro episodio de la atareada vida de Lobatchewsky muestra que no sólo la Matemática consumió su tiempo. La Rusia de 1830 se hallaba en unas condiciones sanitarias tan deplorables como un siglo después, cuando los soldados alemanes, durante la gran guerra, quedaban asombrados al contemplar los infortunados prisioneros rusos. Como era natural, al extenderse la epidemia colérica entre los infelices habitante de Kazan, en los días de Lobatchewsky, prometía reinar allí durante largo tiempo. La teoría infecciosa de los gérmenes era aún desconocida en 1830, aunque los individuos más inteligentes sospechaban ya que la suciedad tenía mucha más intervención en el brote de las pestes que lo que pudiera tener la ira del Señor.

Cuando el cólera invadió Kazan, los sacerdotes hicieron lo que pudieron en favor de aquellas humildes gentes, reuniéndolas en la iglesias para pedirles que unieran sus súplicas, absolviendo a los moribundos y enterrando a los muertos, pero no pensaron que una pala puede también ser útil para más propósitos que el de cavar sepulturas. Dándose cuenta de que la situación de la ciudad era desesperada, Lobatchewsky pidió a sus compañeros que trajeran a sus familias a la Universidad, y luego solicitó, o por mejor decir ordenó, a algunos de sus estudiantes que se unieran a él en una lucha humana y racional contra el cólera. Las ventanas se cerraron herméticamente, se impusieron estrictas medidas sanitarias, y tan sólo se concedieron las salidas necesarias para obtener los alimentos. De los 660 hombres, mujeres y niños así protegidos sólo murieron 16, una mortalidad inferior a 2,5 %. Comparando esta mortalidad con la que tenía lugar en el resto de las gentes que recibían los remedios tradicionales, esa cifra era despreciable.

Podría suponerse que después de todos sus distinguidos servicios en beneficio del Estado y de su reconocimiento como un gran matemático por los profesores europeos, Lobatchewsky recibiría los mayores honores por parte de su gobierno. Imaginar esto no sólo sería pecar de ingenuo, sino que se desobedecería el mandato bíblico "No confiéis en príncipes". Como premio de sus sacrificios y de su lealtad Lobatchewsky fue bruscamente relevado, en 1846, de su cátedra y de su Rectorado. No se dio ninguna explicación de este singular e inmerecido doble insulto. Lobatchewsky tenía 54 años, y su cuerpo y su mente eran más vigorosas que nunca para continuar sus investigaciones matemáticas. Sus colegas protestaron unánimemente contra el ultraje, poniendo en peligro su propia seguridad, pero fueron brevemente informados de que por ser simples profesores, eran constitucionalmente incapaces de comprender los grandes misterios de la ciencia del gobierno.

Esta excusa mal disfrazada abatió a Lobatchewsky. Todavía le fue permitido conservar su estudio en la Universidad. Pero cuando su sucesor, elegido por el gobierno para disciplinar la desafecta facultad, llegó en 1847 para hacerse cargo de su ingrata tarea, Lobatchewsky abandonó toda esperanza de verse repuesto en la Universidad, que debía su importancia casi exclusivamente a sus esfuerzos, y desde entonces sólo apareció contadas veces para asistir a los exámenes. Aunque su vista decayó rápidamente, aun fue capaz de un intenso pensamiento matemático.

Amaba siempre a la Universidad. Su salud se quebrantó al morir su hijo, pero continuó activo con la esperanza de que aun pudiera ser útil. En 1855 la Universidad celebró el cincuentenario de su creación. Para conmemorar este acontecimiento, Lobatchewsky acudió en persona a presentar un ejemplar de su Pangeometría , la obra de su vida científica. Este trabajo (en francés y en ruso) no fue escrito por él, sino dictado, pues Lobatchewsky estaba ciego. Pocos meses más tarde murió, el 24 de febrero de 1856, teniendo 62 años.

Para comprender lo que Lobatchewsky hizo debemos examinar en primer término las notables conquistas de Euclides. Hasta hace poco tiempo el nombre de Euclides era prácticamente sinónimo de Geometría elemental. Del hombre poco se sabía, aparte de las dudosas fechas de su nacimiento y muerte. (330-275 a. J. C,). Además de una explicación sistemática de la Geometría elemental, sus Elementos encierran todo lo que se sabía en su época de la teoría de números. La enseñanza de la geometría ha estado inspirada por Euclides durante más de 2200 años. La labor desarrollada en los Elementos parece haber sido sobre todo la de reunir y exponer lógicamente los resultados de sus predecesores y contemporáneos, y su objeto fue hacer una exposición razonada de la Geometría elemental, de tal modo que cualquiera de las proposiciones contenidas pudiera ser referida a los postulados. Euclides no alcanzó su ideal y ni siquiera nada aproximado, aunque durante siglos se creyó que lo había logrado.

El título de Euclides a la inmortalidad está basado en otra cosa que no es la supuesta perfección lógica que todavía suele atribuírsela erróneamente. Es su reconocimiento de que el quinto de sus postulados (su axioma XI) es una pura suposición. El quinto postulado puede anunciarse de muchas maneras equivalentes, cada una de las cuales puede deducirse de las otras por medio de los restantes postulados de la Geometría de Euclides. Posiblemente, el más sencillo de estos enunciados equivalentes es el siguiente: Dada cualquier línea recta l y un punto P , que no está en l , es posible trazar, en el plano determinado por l y P , tan sólo una línea recta l' pasando por P , de tal modo que l' jamás corte a l por más que se prolonguen ambas líneas l y l en ambos sentidos.

Figura 1.

Como una definición nominal diremos que dos rectas que están en un plano y que no se encuentran son paralelas. Así, el quinto postulado de Euclides afirma que existe una sola línea recta paralela a l que pase por P . La penetrante visión de Euclides respecto a la naturaleza de la Geometría le convenció de que su postulado no se deducía de los otros, aunque habían sido hechos muchos ensayos para demostrar el postulado. Siendo incapaz de deducir el postulado de sus otras suposiciones, y deseando usarlo en las demostraciones de muchos teoremas, Euclides honradamente lo separó de sus otros postulados.

Existen una o dos simples cuestiones de que debemos tratar antes de ocuparnos de la intervención revolucionaria de Lobatchewsky en el campo de la Geometría. Nos referimos a las proposiciones "equivalentes" al postulado de las paralelas. Una de éstas, "la hipótesis del ángulo recto", según se denomina, sugiere otras dos posibilidades, ninguna de las cuales equivale a la suposición de Euclides: una de ellas lleva a la Geometría de Lobatchewsky, la otra a la de Riemann.

Figura 2

Consideremos una figura AXYB que "parece" un rectángulo, compuesta de cuatro segmentos rectos AX, XY, YB, BA, en la cual BA (o AB) es la base, AX y YB (o BY) son iguales y perpendiculares a AB y sobre un mismo lado de AB . Las cosas esenciales que hay que recordar acerca de esta figura son que cada uno de los ángulos XAB, YBA (en la base) es un ángulo recto, y que los lados AX, BY tienen igual longitud. Sin utilizar el postulado de las paralelas puede probarse que los ángulos AXY, BYX son iguales, pero sin utilizar este postulado es imposible demostrar que AXY, BYX son ángulos rectos, aunque lo parezcan. Si aceptamos el postulado de las paralelas, podemos demostrar que AXY, BYX son ángulos rectos, e inversamente, si aceptamos que AXY, BYX son ángulos rectos, podemos demostrar el postulado de las paralelas. Así, la hipótesis de que AXY, BYX son ángulos rectos es equivalente al postulado de las paralelas. Esta hipótesis se llama actualmente la hipótesis del ángulo recto (puesto que ambos ángulos son rectos se usa el singular en vez del plural "ángulos").

Se sabe que la hipótesis del ángulo recto conduce a una Geometría consecuente y prácticamente útil, es decir a la Geometría de Euclides remozada para satisfacer las exigencias modernas del rigor lógico. Pero la figura sugiere otras dos posibilidades: cada uno de los ángulos igua les AXY, BYX es menor que un ángulo recto , hipótesis del ángulo agudo ; cada uno de los ángulos iguales, AXY, BYB es mayor que un ángulo recto , hipótesis del ángulo obtuso . Dado que un ángulo puede satisfacer a una y sólo a una de las exigencias, que es ser igual a, menor que, o mayor que un ángulo recto, las tres hipótesis, del ángulo recto, del ángulo agudo y del ángulo obtuso, respectivamente, agotan las posibilidades.

La experiencia vulgar nos predispone en favor de la primera hipótesis. Para comprender que las dos restantes no son tan irracionales como parecen a primera vista, consideraremos alguna cosa que está más cerca de la experiencia humana real que el "plano" idealizado en el que Euclides imaginaba trazadas sus figuras. Pero primero observemos que ni la hipótesis del ángulo agudo ni la del ángulo obtuso nos permiten demostrar el postulado de las paralelas de Euclides debido a que, como antes hemos dicho, el postulado de Euclides es equivalente a la hipótesis del ángulo recto (en el sentido de que puede deducirse uno de otra; la hipótesis del ángulo recto es necesaria y suficiente para la deducción del postulado de las paralelas). Por tanto, si conseguimos construir geometrías basándonos en cualquiera de las dos nuevas hipótesis, no encontraremos en ellas paralelas en el sentido de Euclides.

Para hacer a las otras hipótesis menos irracionales de lo que parecen a primera vista, supongamos que la Tierra fuera una esfera perfecta (sin las irregularidades debidas a las montañas, etc.). Un plano trazado a través del centro de esta Tierra ideal corta la superficie según una circunferencia máxima. Supongamos que deseamos ir desde un punto A a otro B sobre la superficie de la Tierra, manteniéndonos siempre sobre la superficie al pasar desde A a B, y supongamos además que deseamos hacer el recorrido por el camino más corto posible. Este es el problema de la "navegación según una circunferencia máxima". Imaginemos un plano que pase por A, B y el centro de la Tierra (sólo existe un plano que reúne estas condiciones).

Figura 3.

Este plano corta a la superficie según una circunferencia máxima. Para hacer nuestro viaje más rápido vamos desde A a B siguiendo el arco más corto de los dos arcos de este círculo máximo. Si A, B se encuentran en la extremidad de un diámetro, podemos marchar por ambos arcos. 1 El ejemplo precedente introduce la definición importante de geodésico de una superficie, que ahora vamos a explicar. Se ha visto que el camino más corto que une dos puntos sobre una esfera, medida la distancia sobre la superficie, es un arco de la circunferencia máxima que los une. Hemos visto también que la distancia más larga que une los dos puntos es el otro arco de la misma circunferencia, salvo en el caso en que los puntos sean los extremos de un diámetro, pues entonces, los dos arcos son iguales. Recordaremos ahora que el segmento de recta que une dos puntos en un plano, se define como "la distancia entre esos dos puntos". Trasladando esta definición a la esfera diremos que la línea recta en el plano corresponde a la circunferencia máxima sobre la esfera. Puesto que la palabra griega que significa Tierra es la primera sílaba geo ( g h ) de geodésico, llamaremos a todas las líneas de mínima distancia que unen dos puntos cualesquiera sobre cualquier superficie las geodésicas de esa superficie. Así, en un plano las geodésicas son las líneas rectas de Euclides; sobre una esfera son circunferencias máximas. Una geodésico puede ser representada como la posición tomada por una cuerda extendida lo más tirante posible entre dos puntos sobre una superficie.

Ahora bien, en navegación al menos, la superficie de un océano no se considera como una superficie plana (plano euclidiano), aunque las distancias sean cortas; se la considera como lo que es muy aproximadamente, como una parte de la superficie de una esfera, y la Geometría de la navegación según una circunferencia máxima, no es la de Euclides. La de Euclides no es, pues, la única Geometría de utilidad para el hombre. Sobre el plano dos geodésicas se cortan precisamente en un punto, a no ser que sean paralelas, pues entonces no se cortan (en Geometría euclidiana); pero sobre la esfera dos geodésicas cualesquiera siempre se cortan precisamente en dos puntos. Además, sobre un plano dos geodésicas no pueden encerrar un espacio, tal como acepta Euclides en uno de los postulados de su Geometría; sobre una esfera, dos geodésicas cualesquiera siempre encierran un espacio.

Imaginemos ahora el ecuador sobre la esfera y dos geodésicas trazadas por el polo norte perpendiculares al ecuador. En el hemisferio norte esto da lugar a un triángulo con lados curvos, dos de los cuales son iguales. Cada lado de este triángulo es un arco de geodésico. Tracemos cualquiera otra geodésica que corte los dos lados iguales, de modo que las partes interceptadas entre el ecuador y la línea secante sean iguales. Tenemos ahora, sobre la esfera, la figura de cuatro lados correspondiente a la figura AXYB que hace pocos momentos teníamos en el plano. Los dos ángulos en la base de esta figura son ángulos rectos y los lados correspondientes son iguales, como antes, pero cada uno de los ángulos iguales, en X, Y son ahora mayores que un ángulo recto. Así, en la Geometría extraordinariamente práctica de la navegación según una circunferencia máxima que está más cerca de la experiencia humana real que los esquemas idealizados de la Geometría elemental, no es verdadero el postulado de Euclides, o su equivalente en la hipótesis del ángulo recto, sino la Geometría que se deduce de la hipótesis del ángulo obtuso.

De igual modo, inspeccionando una superficie menos familiar, podemos hacer razonable la hipótesis del ángulo agudo. La superficie semeja dos trompetas infinitamente alargadas, soldadas en sus extremos más anchos.

Figura 4.

Para describir esta figura más exactamente debemos introducir la curva plana llamada tractriz, que se engendra del siguiente modo.

Figura 5.

Tracemos dos rectas XOX', YOY' en un plano horizontal, cortándose perpendicularmente en 0, como en la Geometría cartesiana. Imaginemos un hilo flexible e inextensible a lo largo de YOY', que tiene en un extremo una pequeña esfera pesada, estando el otro extremo en O. Llevar ese extremo a lo largo de la línea OX. En su movimiento, la esfera traza una mitad de la tractriz; la otra mitad se traza llevando el extremo del hilo a lo largo de OX', y como se comprende es simplemente la reflexión o imagen en OY de la primera mitad. Se supone que el trazado continúa indefinidamente, "hasta el infinito", en cada caso. Ahora imaginemos que la tractriz gira alrededor de la línea XOX'. Se engendra la superficie en doble trompeta; por razones que no necesitamos detallar (tiene curvatura negativa constante) se llama una pseudoesfera. Si sobre esta superficie trazamos la figura de cuatro lados iguales y dos ángulos rectos como antes, usando geodésicas, encontramos realizada la hipótesis del ángulo agudo.

Así, las hipótesis del ángulo recto, del ángulo obtuso y del ángulo agudo respectivamente, son verdaderas sobre un plano euclidiano, sobre una esfera y sobre una pseudoesfera y en todos los casos las "líneas rectas" son geodésicas. La Geometría euclidiana es un caso límite o degenerado de la Geometría sobre una esfera, que se alcanza cuando el radio de la esfera se hace infinito.

En lugar de construir una Geometría adaptada a la Tierra que los seres humanos conocemos ahora, Euclides aparentemente partió de la suposición de que la Tierra es plana. Si Euclides no lo hizo, sus predecesores lo hicieron, y por aquella época la teoría del "espacio" o Geometría le llevó a las escuetas suposiciones que enuncia en sus postulados considerados como verdades necesarias e inmutables, reveladas a la humanidad por una inteligencia superior como la verdadera esencia de todas las cosas materiales. Fueron necesarios más de 2000 años para derribar la eterna verdad de la Geometría, y Lobatchewsky lo consiguió.

Para usar la frase de Einstein, Lobatchewsky contradijo un axioma. Quien contradice una "verdad aceptada" que ha parecido necesaria o razonable a la gran mayoría de los hombres durante dos mil años o más, pone en peligro su reputación científica, y quizá su vida. Einstein mismo contradijo el axioma de que dos acontecimientos pueden ocurrir en diferentes lugares al mismo tiempo, y analizando esta suposición llegó a inventar la teoría especial de la relatividad. Lobatchewsky contradijo la hipótesis del postulado de las paralelas de Euclides o, lo que es equivalente, la hipótesis del ángulo recto, afirmando que no es necesaria para una Geometría consecuente, y fundó su contradicción estableciendo un sistema de Geometría basada sobre la hipótesis del ángulo agudo en la que por un punto dado no sólo puede trazarse una paralela a una recta dada, sino dos. Ninguna de las paralelas de Lobatchewsky corta la línea a la que ambas son paralelas, ni tampoco cualquier línea recta trazada por el punto dado y que está dentro del ángulo formado por las dos paralelas. Esta al parecer extraña situación se "realiza" para las geodésicas de una pseudoesfera.

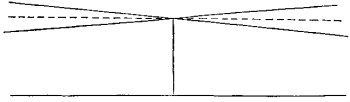
Figura 6

Para cualquier propósito de la vida diaria (medida de distancias, etc.), las diferencias entre las geometrías de Euclides y Lobatchewsky son demasiado pequeñas para ser tenidas en cuenta, pero no es éste el punto importante; cada una tiene importancia por sí misma, y cada una de ella es adecuada para las experiencias humanas. Lobatchewsky abolió la "verdad" necesaria de la geometría euclidiana. Su Geometría fue la primera de las diversas geometrías construidas por sus sucesores. Algunos de estos sustitutos de la Geometría euclidiana, por ejemplo la Geometría de Rieman o de la relatividad general, son hoy, al menos, tan importantes para aquella parte de la ciencia física que se está desarrollando como era la de Euclides en las partes clásicas, relativamente estáticas. Para algunos fines, la Geometría de Euclides es mejor, o al menos suficiente; para otros no es adecuada y se precisa una geometría no euclidiana.

Durante 2200 años se creyó, en cierto sentido, que Euclides había descubierto una verdad absoluta o una forma necesaria de percepción humana en su sistema de Geometría. La creación de Lobatchewsky fue una pragmática demostración del error de esta creencia. La audacia de su oposición y su triunfo han conducido a los matemáticos y a los científicos en general a contradecir otros axiomas o verdades aceptadas, por ejemplo la ley de causalidad que durante siglos pareció tan necesaria para el pensamiento como el postulado de Euclides parecía hasta que fue eliminado por Lobatchewsky.

Es probable que todavía no se haya hecho sentir totalmente la conmoción producida por el método de Lobatchewsky de negar los axiomas. No hay exageración en llamar a Lobatchewsky el Copérnico de la Geometría, pero la Geometría es sólo una parte del más amplio campo que renovó. Por ello sería más justo denominarle el Copérnico de todo el pensamiento.