C O N T E N I D O
Aclaraciones
Citas
1. Introducción
2. Zenón, Eudoxio y Arquímedes
3. Descartes
4. Fermat
5. Pascal
6. Newton
7. Leibniz
8. Los Bernoulli
9. Euler
10. Lagrange
11. Laplace
12. Monge y Fourier
13. Poncelet
14. Gauss
15. Cauchy
16. Lobatchewsky
17. Abel
18. Jacobi
19. Hamilton
20. Galois
21. Silvester
22. Weierstrass y Sonja Kowalewsky
23. Boole
24. Hermite
25. Kronecker
26. Riemann
27. Kummer y Dedekind
28. Poincaré
29. Cantor
Bajar Parte 1
Bajar Parte 2
Bajar Parte 3
EL HOMBRE, NO EL METODO
HERMITE
|
Hablad con M. Hermite: jamás evoca una imagen concreta: sin embargo, se percibe
inmediatamente que las entidades más abstractas son para él como criaturas
vivientes.
Henri Poincaré |
Los problemas importantes no resueltos exigen nuevos métodos para su solución, mientras los nuevos y poderosos métodos piden nuevos problemas para ser resueltos. Mas como Poincaré observó, es el hombre, no el método, el que resuelve un problema.
De los antiguos problemas causantes de nuevos métodos en Matemática, el del movimiento, y todo lo que esto implica para la mecánica, terrestre y celeste, puede ser recordado como uno de los principales instigadores del Cálculo, y al presente intenta establecer el razonamiento acerca del infinito sobre una base firme. Un ejemplo de nuevos problemas sugeridos por los nuevos métodos es el enjambre que el cálculo sensorial, popularizado entre los geómetras por sus resultados en la relatividad, planteó en la Geometría. Y, finalmente, con una confirmación de la observación de Poincaré, recordaremos que fue Einstein y no el método de los tensores quien resolvió el problema de dar una explicación matemática consecuente de la gravitación. Las tres tesis se encuentran reunidas en la vida de Charles Hermite, el principal matemático francés de la segunda mitad del siglo XIX, haciendo excepción de Poincaré, discípulo de Hermite, que pertenece en parte a nuestro propio siglo.
Charles Hermite, nacido en Dieuze, Lorena, Francia, el 24 de diciembre de 1822, difícilmente pudo haber elegido un momento más propicio para su nacimiento que la tercera década del siglo XIX. En ese momento se precisaba la rara combinación del genio creador y la capacidad para comprender la obra de los otros investigadores con objeto de coordinar las creaciones aritméticas de Gauss con los descubrimientos de Abel y Jacobi en las funciones elípticas, los notables progresos de Jacobi en las funciones abelianas y la vasta teoría de invariantes algebraicos que los matemáticos ingleses Boole, Cayley y Sylvester estaban desarrollando rápidamente.
Hermite casi perdió su vida en la Revolución francesa, aunque la última cabeza rodó casi un cuarto de siglo antes de que él hubiera nacido. Su abuelo paterno fue arruinado por la Commune y murió en prisión. El hermano del abuelo fue guillotinado. El padre de Hermite escapó debido a su juventud.
Si la capacidad matemática de Hermite fue heredada y probablemente procede del padre, quien estudió ingeniería. No encontrando placer por los estudios de ingeniería, Hermite padre renunció a ellos, y después de una iniciación igualmente errónea en la industria de la sal, terminó como comerciante en tejidos. Esta profesión fue, sin duda, elegida por el hecho de haberse casado con la hija de su patrón, Madeleine Lallemand, una mujer dominante que llevaba las riendas de su familia, y que mandaba en todo, desde el negocio hasta su marido. Consiguió establecer una posición de sólida prosperidad burguesa. Charles fue el sexto de siete hijos, cinco de sexo masculino y dos de sexo femenino. Nació con una deformidad de la pierna derecha, que le hizo cojear durante toda la vida, posiblemente una suerte para él pues fue un obstáculo para cualquier carrera relacionada con el ejército, y siempre tuvo que usar bastón. Su deformidad nunca afectó la uniforme dulzura de su carácter.
La primera educación de Hermite corrió a cargo de sus padres. Como el negocio seguía prosperando, la familia se traslado desde Dieuze a Nancy, cuando Hermite tenía 6 años. Luego, las exigencias cada vez mayores del negocio absorbieron todo el tiempo de los padres, y Hermite fue enviado al Liceo de Nancy. Como esta escuela no les pareciera adecuada a los padres, cada vez más enriquecidos, decidieron enviar a Charles a París. Allí estudió durante breve tiempo en el Liceo Henry IV, y de allí pasó, cuando tenía 18 años, al más famoso (o más infame) Louis-le-Grand, el "Alma Mater" del pobre Galois, para ingresar en la Politécnica.
Durante cierto tiempo pareció que Hermite iba a repetir el desastre de su indómito predecesor en Louis-le-Grand. Sentía la misma repugnancia por la retórica y la misma indiferencia para la Matemática elemental. Pero las buenas conferencias sobre Física le fascinaban, y pronto prestó su cordial cooperación en el proceso bilateral de adquirir una educación. Más tarde, cuando ya no era molestado por los pedantes, Hermite llegó a conocer el griego y el latín, y escribía una prosa bella y clara.
Quienes están en contra de los exámenes podrán encontrar un argumento en Hermite. En las carreras de estos dos famosos alumnos de Louis-le-Grand, Galois y Hermite, se encuentra algo que debe hacer meditar a quienes creen que los exámenes son una excelente medida para ordenar a los seres humanos según sus métodos intelectuales. Habrá que preguntarse si esos defensores han empleado sus cabezas o sus pies para llegar a tal conclusión.
Tan sólo por la gracia de Dios y por la diplomática persistencia del inteligente profesor Richard, que había hecho cuanto pudo, 15 años antes, para salvar a Galois, Hermite no fue rechazado por los estúpidos jueces. Siendo aún estudiante en el Liceo, Hermite, siguiendo los pasos de Galois, sustituía las lecciones elementales por la lectura privada en la biblioteca de Sainte-Gene-Yiéve, donde leyó la memoria de Lagrange sobre la resolución de las ecuaciones numéricas. Con sus ahorros compró la traducción francesa de las Disquisiliones Arithmeticae de Gauss, y, lo que es más, las comprendió como pocos las han comprendido antes y las comprenderán en el futuro. Por esa época, conociendo lo que Gauss había hecho, Hermite estaba preparado para seguir adelante. "Fue en estos dos libros, solía decir en su vida ulterior, donde aprendí álgebra". Euler y Laplace también le instruyeron a través de sus obras. Sin embargo, el comportamiento de Hermite en los exámenes fue mediocre, por emplear la calificación más halagadora posible.
Recordando el trágico fin de Galois, Richard intentó apartar a Hermite de las investigaciones originales, y conducirle a través de las aguas más fangosas de los exámenes para que ingresara en la Escuela Politécnica, la sucia zanja en la que Galois se ahogó. De todos modos, el buen Richard no pudo menos de decir al padre de Hermite que Charles era "un joven Lagrange".
Los Nouvelles Annales de Mathématiques, una revista dedicada a los estudiantes de las escuelas superiores, fueron fundados en 1842. El primer volumen contiene dos trabajos compuestos por Hermite cuando todavía estudiaba en Louis-le-Grand. El primero es un simple ejercicio de Geometría analítica sobre secciones cónicas, y no muestra gran originalidad. El segundo, que ocupa tan sólo seis páginas y media en las obras completas de Hermite, es algo muy diferente. Su título era: Consideraciones sobre la solución algebraica de la ecuación de quinto grado.
"Es sabido, comienza diciendo el modesto matemático de 20 años, que Lagrange hizo depender la solución algebraica de la ecuación general de quinto grado de la determinación de una raíz y de una ecuación particular de sexto grado, que llamó una ecuación reducida [en la actualidad una resolvente]... De modo que si la resolvente se descompone en factores racionales de segundo o tercer grado, tendremos la solución de la ecuación de quinto grado. Intentaré probar que tal descomposición es imposible". Hermite no sólo consiguió esta demostración con un bello y simple argumento, sino también mostró al hacer esto que era un algebrista. Con pocos y ligeros cambios este breve trabajo muestra lo que se requiere para tal operación.
Puede parecer extraño que un joven capaz de seguir el razonamiento matemático, según demostró Hermite en su trabajo sobre la quíntica general, pueda encontrar dificultades en la Matemática elemental. Per no es necesario comprender, ni siquiera oír hablar, de gran parte de la Matemática clásica desarrollada en el curso de su larga historia, para ser capaz de seguir o hacer obra creadora en la Matemática que se ha desarrollado desde el año 1800, y es aun de vivo interés para los matemáticos. El tratamiento geométrico (sintético) de las secciones cónicas de los griegos, por ejemplo, no necesita ser comprendido por quienes actualmente desee estudiar la Geometría moderna; ni se necesita Geometría alguna para quien guste de los estudios algebraicos o aritméticos. En menor grado puede decirse lo mismo para el Análisis, donde el lenguaje geométrico usado es el más sencillo, no siendo necesario ni deseable cuando se trata de las demostraciones modernas. Como último ejemplo recordaremos que la Geometría descriptiva, de gran utilidad para los ingenieros, no tiene prácticamente utilidad para los que se dedican a la Matemática. Algunos de los temas más difíciles de la Matemática, que aun se plantean, exigen tan sólo un ligero conocimiento del álgebra y una clara inteligencia para su comprensión. Tales son la teoría de grupos finitos, la teoría matemática del infinito y parte del Cálculo de probabilidades y de la Aritmética superior. No es, pues, asombroso que los amplios conocimientos que se exigen a un candidato para el ingreso en una escuela técnica científica o hasta para obtener un título en tales escuelas, sean poco menos que inútiles para la carrera matemática. Esto explica los triunfos espectaculares de Hermite como matemático creador, y su dificultad para escapar del completo desastre ante el tribunal de exámenes.
Más tarde, en 1842, teniendo 20 años, Hermite se presentó a los exámenes de ingreso de la Escuela Politécnica. Pasó, pero ocupando el lugar 68 en orden de mérito. Por entonces ya era mejor matemático que algunos de sus jueces. El resultado humillante de sus exámenes causó una impresión sobre el joven maestro que jamás pudo ser borrada por todos los triunfos obtenidos más tarde.
Hermite permaneció sólo un año en la Politécnica. No fue eliminado por falta de conocimientos, sino por su pie anormal, que, de acuerdo con las disposiciones, le hacían incapaz para ocupar los cargos a que tenían derecho los estudiantes brillantes de la Politécnica. Quizá haya sido un bien para Hermite la expulsión de la Escuela; su ardiente patriotismo quizá le hubiera hecho mezclarse en una u otra de las reyertas políticas o militares tan queridas al efervescente temperamento francés. Sin embargo, el año no había sido perdido. En lugar de dedicarse a la Geometría descriptiva, por la que sentía profundo odio, Hermite empleó su tiempo en el estudio de las funciones abelianas, que en aquella época (1842) quizá era el tema de mayor interés e importancia para los grandes matemáticos de Europa. También pudo conocer a Joseph Liouville (1809-1882) un matemático de primera categoría y editor del Journal des Mathématiques.
Liouville reconoció el genio de Hermite en cuanto lo vio. De pasada recordaremos que Liouville inspiró a William Thomson, Lord Kelvin, el famoso físico escocés, una de las más notables definiciones de lo que es un matemático. "¿Sabéis qué es un matemático?", preguntó una vez Kelvin en la clase. Se levantó, se acercó al pizarrón, y escribió:
Colocando su dedo sobre lo que había escrito, se dirigió a la clase: "Un matemático es un individuo para quien esto es tan conocido como lo es para vosotros el hecho de que dos y dos son cuatro. Liouville era un matemático". Por lo que se refiere al grado de dificultad, la obra del joven Hermite en las funciones abelianas, comenzada antes de que tuviera 21 años, está con respecto a la fórmula de Kelvin en una relación igual a la que existe entre tal fórmula y el conocido ejemplo de "2 y 2 son cuatro". ¡Recordando la cordial bienvenida que el anciano Legendre acordó a la obra revolucionaria del joven y desconocido Jacobi, Liouville pensó que Jacobi mostraría igual generosidad para Hermite, que entonces iniciaba su trabajo. No se equivocó.
La primera de las cartas de Hermite a Jacobi está fechada en París, en el mes de enero de 1843. "Vuestra memoria sobre las funciones periódicas cuádruples surgida en la teoría de funciones abelianas, me ha llevado a un teorema, para la división de los argumentos [variables] de estas funciones, análogo al que habéis establecido... para obtener la expresión más simple de las raíces de las ecuaciones tratadas por Abel. M. Liouville me ha incitado a escribiros para someter este trabajo a vuestra consideración. Al hacerlo, Señor, espero seáis tan amable que lo recibáis con toda la indulgencia que necesita". Así comienza su labor en la Matemática.
Recordaremos brevemente la simple naturaleza del problema en cuestión: las funciones trigonométricas son funciones de una variable con un período; por tanto sen ( x + 2 p ) = sen x , donde x es la variable y 2 n es el período. Abel y Jacobi, "invirtiendo" las integrales elípticas, describieron funciones de una variable y dos períodos, o sea f(x + p + q ) = f(x), donde p, q son los períodos (véase capítulos 12, 18). Jacobi descubrió funciones de dos variables y cuatro períodos, o sea
donde a, b, c, d son los períodos. Un problema que pronto se encuentra en Trigonometría es expresar
o
,
o de un modo general
donde n es un número entero, en función de sen x (y posiblemente otras funciones trigonométricas de x). El problema correspondiente para las funciones de dos variables y cuatro períodos, fue el que Hermite abordó. En el problema trigonométrico somos finamente llevados a ecuaciones muy sencillas; en el problema incomparablemente más difícil de Hermite el resultado es además una ecuación (de grado n 4 ), y lo inesperado acerca de esta ecuación es que se puede resolver algebraicamente, es decir, por radicales.
Eliminado de la Politécnica por su cojera, Hermite puso sus ojos en la profesión docente como un medio donde poder ganar su sustento, mientras continuaba trabajando en su amada Matemática. La carrera docente se abría ante él, tuviera o no título, pero las reglas y disposiciones eran inexorables, y no hacían excepciones. La rutina oficinesca en forma de balduque siempre amenaza al hombre que sigue una senda equivocada, y casi estranguló a Hermite.
Incapaz de curarse de su "perniciosa originalidad", Hermite continuó sus investigaciones hasta el momento en que, teniendo 24 años, tuvo que abandonar los descubrimientos fundamentales para llegar a comprender las trivialidades requeridas para la enseñanza elemental (bachilleres de artes y ciencias). Dos pruebas más difíciles debían completar la primera antes de que el joven genio matemático obtuviera el certificado para dedicarse a la enseñanza, pero, por fortuna, Hermite escapó de la última y peor cuando algunos amigos influyentes le nombraron para un cargo donde podía burlarse de los examinadores. Pasó sus exámenes (en 1847-48) muy difícilmente. Pero sin la cordialidad de dos de los inquisidores, Sturm y Bertrand, buenos matemáticos que reconocieron en él a un excelente investigador en cuanto lo vieron es probable que Hermite no hubiera sido aprobado. (Hermite se casó con Louise, hermana de Bertrand, en 1848).
Por un irónico capricho del destino el primer triunfo académico de Hermite fue su nombramiento, en 1848, como juez para los exámenes de admisión en la Politécnica, en la que casi había sido rechazado. Pocos meses más tarde fue nombrado repetidor en la misma institución. Se encontraba ahora seguro, en un lugar donde ningún juez podía hacer liada contra él. Pero para llegar a esta "triste eminencia", y adaptarse a las estupideces del sistema oficial, había tenido que sacrificar casi cinco años de lo que seguramente fue el período de su mayor capacidad inventiva.
Finalmente, habiendo satisfecho a sus crueles examinadores, o habiéndose evadido de ellos, Hermite se encontraba en condiciones para llegar a ser un gran matemático. Su vida era pacífica. Desde 1848 hasta 1850 sustituyó a Libri en el Collège de France. Seis años más tarde, teniendo 34 años, fue elegido miembro de la Academia de Ciencias. A pesar de su reputación mundial como matemático creador fue necesario que pasaran 47 años, antes de que obtuvieran un cargo adecuado. Fue nombrado profesor en la Escuela Normal tan sólo en 1869 y, finalmente, en 1870 fue profesor en la Sorbona, cargo que mantuvo hasta su retiro, 27 años más tarde. Durante el tiempo que ocupó este influyente cargo enseñó a toda una generación de distinguidos matemáticos franceses, entre los que mencionaremos a émile Picard, Gaston Darboux, Paul Appell, émile Borel, Paul Painlevé y Henri Poincaré. Pero su influencia se extendió mas allá de Francia, y sus trabajos clásicos ayudaron a educar a sus contemporáneos en todos los países.
Un rasgo especial de la bella obra de Hermite está íntimamente relacionado con su repugnancia a aprovecharse de su influyente posición para formar a todos sus discípulos siguiendo su propia imagen. Esta es la inextinguible generosidad que invariablemente derrochó entre sus colegas los matemáticos. Probablemente, ningún otro matemático de los tiempos modernos ha mantenido una correspondencia científica tan voluminosa con todos los investigadores de Europa como Hermite, y en todas sus cartas es siempre cordial y alentador. Muchos de los matemáticos de la segunda mitad del siglo XIX le deben mucho a la publicidad que Hermite dio a sus primeros estudios. En este, como en otros respectos, no hay un carácter más delicado en toda la historia de la Matemática. Jacobi fue tan generoso como él, con la sola excepción de la primera acogida que dispensó a Eisenstein, pero tenía una tendencia al sarcasmo (muchas veces extraordinariamente divertido, salvo para la infeliz víctima), que estaba totalmente ausente en el genial francés. Hermite fue digno de la generosa observación de Jacobi cuando el desconocido joven matemático se aventuró a acercarse a él con su primera gran obra sobre las funciones abelianas. "No se desconcierte señor, escribía Jacobi, si algunos de sus descubrimientos coinciden con otros que yo he hecho hace tiempo. Como debéis comenzar donde yo terminé, debe existir necesariamente una pequeña esfera de contacto. En el futuro, si me honráis con vuestras comunicaciones, sólo tendré ocasión de aprender".
Alentado por Jacobi, Hermite no sólo le hizo conocer su trabajo, sobre las funciones abelianas, sino que le envió cuatro enormes cartas sobre la teoría de números, la primera en 1847. Estas cartas, la primera de las cuales fue escrita cuando Hermite tenía 24 años, abre nuevos caminos (como luego veremos), y bastaría para que Hermite fuera considerado como un matemático creador de primera categoría. La genialidad de los problemas que abordó y la audaz originalidad de los métodos ideados para su solución, aseguran que Hermite sea recordado como uno de los matemáticos innatos de la historia.
La primera carta se inicia con una excusa. "Han transcurrido casi dos años sin haber dado respuesta a la carta que me hicisteis el honor de escribirme. Hoy le pido perdón por mi negligencia y quiero expresarle toda la alegría que siento al verme ocupar un lugar en el repertorio de vuestras obras. [Jacobi publicó parte de la carta de Hermite, dándole la importancia que merecía, en algunas de sus obras]. Habiendo estado alejado durante largo tiempo del trabajo, he quedado profundamente conmovido por esa prueba de vuestra cordialidad; permitidme, señor, creer que no me abandonaréis". Hermite añade luego que otra investigación de Jacobi le inspiró los trabajos que estaba realizando.
Si el lector examina lo que hemos dicho acerca de las funciones uniformes de una sola variable en el capítulo sobre Gauss (una función uniforme toma sólo un valor para cada valor de la variable), podrá comprender la siguiente exposición acerca de lo que Jacobi demostró: una función uniforme de solo una variable con tres periodos diferentes es imposible. El hecho de que existan funciones uniformes de una variable que tienen un período o dos períodos queda demostrado recurriendo a las funciones trigonométricas y a las funciones elípticas. Este teorema de Jacobi, declara Hermite le sugirió su idea para los nuevos métodos que introdujo en Aritmética superior. Aunque estos métodos son demasiado técnicos para explicarlos en este lugar, se puede resumir brevemente el espíritu de uno de ellos.
La Aritmética, en el sentido de Gauss, se ocupa de las propiedades de los números enteros racionales 1, 2, 3...;los irracionales (como la raíz cuadrada de 2)son excluidos. Gauss investigó, en particular, las soluciones en números enteros de amplias clases de ecuaciones indeterminadas con dos o tres incógnitas, por ejemplo,
donde a, b, c, m son números enteros, y es necesario tratar todas las soluciones x, y , de la ecuación en números enteros. El punto que hay que señalar aquí es que el problema se plantea y se resuelve completamente en el campo de los enteros racionales, es decir en el reino del número discontinuo. Utilizar el Análisis, que está adaptado a la investigación de números continuos, a tal problema discontinuo parecería una imposibilidad, pero esto es lo que Hermite logró. Partiendo de una fórmula discontinua, aplicó el Análisis al problema, y finalmente obtuvo resultados en el terreno discontinuo del cual había partido. Como el Análisis está mucho más desarrollado que cualquiera de las técnicas discontinuas inventadas para el álgebra y la Aritmética, el progreso de Hermite fue comparable a la introducción de la maquinaria en las industrias medievales.
Hermite tenía a su disposición una maquinaria mucho más poderosa, tanto algebraica como analítica, que la que estaba a la disposición de Gauss cuando escribió las Disquisitiones Arithmeticae. Con la gran invención de Hermite, estos instrumentos más modernos le capacitaron para abordar problemas que habían desconcertado a Gauss en 1800. En un solo paso Hermite recogió los problemas generales del tipo que Gauss y Eisenstein habían planteado, y al fin comenzó el estudio aritmético de las formas cuadráticas con cualquier número de incógnitas. La naturaleza general de la "teoría de formas" aritmética puede apreciarse en el enunciado de un problema especial. En lugar de la ecuación gaussiana
de segundo grado con dos incógnitas ( x, y ), se requiere tratarlas soluciones en números enteros de ecuaciones similares de grado n, con s incógnitas donde n, s son números enteros, y el grado de cada término en la primera parte de la ecuación es n (no 2como en la ecuación de Gauss). Después de meditar atentamente sobre el hecho de que las investigaciones de Jacobi acerca de la periodicidad de las funciones uniformes dependen de cuestiones más profundas referentes a la teoría de las formas cuadráticas, Hermite bosquejó su programa.
"Pero una vez llegado a este punto de vista, los problemas, suficientemente amplios, que pensé proponer me parecieron sin importancia al lado de las grandes cuestiones de la teoría general de formas. En este ilimitado campo de investigaciones que Monsieur Gauss [Gauss vivía aún cuando Hermite escribía estas palabras y de aquí el cortés "Monsieur"] nos ha abierto, el álgebra y la teoría de números parecen necesariamente fundirse en el mismo orden de los conceptos analíticos de los cuales nuestro presente conocimiento no nos permite aún formarnos una idea exacta".
Hace entonces una observación que, aunque no muy clara, puede interpretarse suponiendo que la clave para las sutiles relaciones entre el álgebra, la Aritmética superior y ciertas partes de la teoría de funciones, se encontrará en una completa comprensión de ese tipo de "números" que son necesarios y suficientes para la solución explícita de todos los tipos de ecuaciones algebraicas. Así para x 3 - 1 = 0, es necesario y suficiente comprender
; para
x
5
+ a
x + b = 0,
donde
a, b
son números dados, ¿qué tipo de "número"
x
debe ser inventado para que
x
pueda ser expresado
explícitamente
en función de
a, b?
Gauss, como es natural, dio un tipo de respuesta: Cualquier raíz
x
es un número complejo. Pero esto es sólo un comienzo. Abel demostró que si
únicamente se permite un número
finito
de operaciones racionales y extracciones de raíces, no hay fórmula explícita
que dé
x
en función de
a, b.
Volveremos a ocuparnos más tarde de esta cuestión. Parece que Hermite, ya muy
precozmente (1848, teniendo 26 años), albergaba en su cabeza uno de sus grandes
descubrimientos.
En su actitud ante los números, Hermite respetaba místicamente la tradición de Pitágoras y Descartes, el credo matemático de este último, como veremos en seguida, era esencialmente pitagórico. En otras cuestiones, el suave Hermite mostró una marcada inclinación hacia el misticismo. A los 43 años era una agnóstico tolerante, como muchos hombres de ciencia franceses de su época. Luego, en 1856, cayó repentinamente enfermo, y, aprovechando su estado, el ardiente Cauchy, que siempre había deplorado que su brillante y joven amigo tuviera un criterio liberal sobre las materias religiosas, cayó sobre el postrado Hermite, y le convirtió al catolicismo romano. Desde entonces Hermite fue un católico devoto, y la práctica de su religión le proporcionó grandes satisfacciones.
El misticismo por los números de Hermite es bastante innocuo, y es una de las características personales sobre las que todo argumento seria vano. Brevemente, Hermite creía que los números tienen una existencia por sí mismos, por encima de todo control humano. Las Matemáticas, pensaba, pueden tener en ciertas ocasiones algún destello de las armonías sobrehumanas que regulan este reino etéreo de la existencia lo mismo que los grandes genios de la ética y de la moral tienen algunas veces la visión de las perfecciones del reino de los cielos.
Puede afirmarse, probablemente, que ningún notable matemático actual que haya prestado cierta atención a lo realizado en los últimos 50 años (especialmente en los últimos 25), para intentar comprender la naturaleza de la Matemática y el proceso del razonamiento matemático estará d e acuerdo con el místico Hermite. Dejamos a juicio del lector resolver si este moderno escepticismo es una ventaja o una desventaja, en comparación con el credo de Hermite. "La existencia matemática", que se considera ahora casi universalmente por los jueces competentes como un concepto erróneo, fue tan admirablemente expresado por Descartes en su teoría del triángulo eterno, que sus palabras pueden ser citadas aquí como un epítome de las creencias místicas de Hermite.
"Imagino un triángulo, aunque quizá tal figura no existe ni ha existido jamás en ninguna parte del mundo fuera de mi pensamiento. De todos modos, esta figura tiene cierta naturaleza o forma o determinada esencia que es inmutable o eterna que yo no he inventado y que no depende de mi mente. Así se aprecie el hecho de que puedo demostrar diversas propiedades de este triángulo, por ejemplo que la suma de sus tres ángulos interiores es igual a dos ángulos rectos, que el ángulo mayor es el que se opone al lado mayor, y así sucesivamente.
Lo desee o no, reconozco de un modo muy claro y convincente que estas propiedades se hallan en el triángulo, aunque jamás haya pensado antes acerca de ellas, y aunque esta sea la primera vez que he imaginado un triángulo. De todos modos, nadie puede decir que yo las he inventado o imaginado". Trasladar "verdades eternas" tan simples como 1 + 2 = 3, 2 + 2 = 4, a la Geometría perdurable de Descartes, constituyó la Aritmética sobrehumana de Hermite.
Una investigación aritmética de Hermite, aunque más bien de tipo técnico, puede ser mencionada aquí como un ejemplo del aspecto profético de la Matemática pura. Recordaremos que Gauss introdujo los enteros complejos (números de la forma, a + bi, donde a, b son enteros racionales e i denota
) en la Artimética superior para dar a la ley de la reciprocidad cuadrática su
más simple expresión. Dirichlet y otros continuadores de Gauss estudiaron luego
las formas cuadráticas en las cuales los enteros racionales que aparecen como
variables y coeficientes son reemplazados por enteros complejos gaussianos.
Hermite pasó al caso general de este tipo e investigó la representación de los
enteros en lo que actualmente se denomina formas de Hermite. Un ejemplo de una
de tales formas (para el caso especial de dos variables complejas
x
1
,
x
2
y sus "conjugadas"
x
1
,
x
2
en lugar de
n
variables) es
en la cual la línea sobre la letra que denota un número complejo indica el conjugado de ese número; es decir, si x + iy es un número complejo su "conjugado", es x - iy ; y los coeficientes a ll , a 12 , a 21 , a 22 son tales que a ij = a ji para
de modo que a 12 y a 21 son conjugados, y cada uno de a ll , a 22 es su propio conjugado (por tanto a 11 , a 22 son números reales). Se aprecia fácilmente que toda la forma es real (libre de i ) si todos los productos se multiplican, pero ésta se expresa más "naturalmente" en la forma dada.
Cuando Hermite inventó tales formas estaba interesado en encontrar qué números están representados por las formas. Setenta años más tarde se encontró que el álgebra de las formas de Hermite es indispensable en la física matemática, particularmente en la moderna teoría de los cuantos. Hermite no tenía la menor idea de que su matemática pura tendría valor para la ciencia mucho tiempo después de su muerte.
En efecto, al igual que Arquímedes, jamás le importaron nada las aplicaciones científicas de la Matemática. Pero el hecho de que la obra de Hermite haya dado a la Física un instrumento útil, es quizá otro argumento en favor de quienes creen que los matemáticos justifican del mejor modo su existencia abstracta cuando se abandonan a sus propios e inescrutables recursos.
Dejando aparte los espléndidos descubrimientos de Hermite en la teoría de invariantes algebraicos, por ser demasiado técnica para ser expuesta en este lugar, nos ocuparemos de dos de sus más espectaculares conquistas en otros campos. La alta estima que la obra de Hermite de invariantes mereció de sus contemporáneos se aprecia, claramente en las palabras de Sylvester: "Cayley, Hermite y yo constituimos una Trinidad Invariante". Sylvester no llega a decir qué papel desempeñó cada uno de ellos en esta asombrosa Trinidad, pero poco importa, pues es posible que cada uno de los miembros de este trébol fuera capaz de transformarse en sí mismo o en cualquiera de los otros dos seres coinvariantes.
Los dos campos donde Hermite encontró lo que quizá sean los resultados individuales más notables de toda su bella obra, corresponden a la ecuación general de quinto grado y a los números trascendentes. Sus hallazgos referentes al primer problema resaltan claramente en la introducción a su breve nota Sur la resolution de l'équation du cinquéme degré. (Sobre la solución de la ecuación [general] de quinto grado), publicada en las Comptes rendus de l'Académie des Sciences en 1858 cuando Hermite tenía 36 años.
"Es sabido que la ecuación general de quinto grado puede ser reducida por una sustitución (de la incógnita x ) de coeficientes dados sin el uso de otro radical que las raíces cuadradas o raíces cúbicas, a la forma:
[Esto es, si podemos resolver esta ecuación, podremos resolver la ecuación general de quinto grado].
"Este notable resultado, debido al matemático inglés Jerrard, es el paso más importante que se ha dado en la teoría algebraica de las ecuaciones de quinto grado desde que Abel demostró que es imposible una solución por radicales. Esta imposibilidad muestra, en efecto, la necesidad de introducir algún nuevo elemento analítico [algún nuevo tipo de función] para buscar la solución, y en este sentido parece natural considerar como un auxiliar las raíces de la ecuación muy simple que hemos mencionado. De todos modos, para justificar rigurosamente su uso como un elemento esencial en la solución de la ecuación general, queda por ver siesta simplicidad deformas realmente nos permiten llegar a alguna idea de la naturaleza de sus raíces, captar lo que es peculiar y esencial en la forma de existencia de estas cantidades, de las cuales nada se sabe más allá del hecho de que no son expresables por radicales.
"Ahora bien, es muy notable que la ecuación de Jerrard se preste con la mayor facilidad a esta investigación, y es, en el sentido que explicaremos, susceptible de una solución analítica real. Podemos, en efecto, concebir la cuestión de la solución algebraica de las ecuaciones desde un punto de vista diferente del que durante largo tiempo se ha seguido para la solución de ecuaciones de los cuatro primeros grados, y que nosotros hemos utilizado especialmente. En lugar de expresar el sistema íntimamente relacionado de raíces, considerado como funciones de los coeficientes, por una fórmula que englobe radicales de múltiples valores, podemos intentar obtener las raíces expresadas separadamente por tantas funciones uniformes diferentes [de un solo valor] de variables auxiliares, como en el caso del tercer grado. En este caso, cuando la ecuación
está en discusión, basta, como sabemos, representar el coeficiente a por el seno de un ángulo, o sea A, para que las raíces sean aisladas como las siguientes funciones bien determinadas
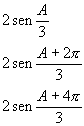
[Hermite recuerda aquí la conocida "solución trigonométrica" de la cúbica ordinariamente estudiada en el segundo curso de álgebra elemental. La "variable auxiliar" es A; las "funciones uniformes" son aquí senos].
"Ahora bien, hay un hecho muy semejante que tenemos que mencionar referente ala ecuación
Sólo que en lugar de senos y cosenos es necesario recurrir a las funciones elípticas..."
Hermite procedió luego a resolver la ecuación general de quinto grado, usando para este fin las funciones elípticas (estrictamente, funciones modulares elípticas, pero la distinción no tiene importancia aquí). Es casi imposible comprender por quien no sea matemático la brillantez espectacular de tal hazaña. Para citar un símil que en realidad no es adecuado, Hermite encontró la famosa "armonía perdida" cuando ningún mortal tenía la más breve sospecha de que existiera en alguna parte en el tiempo y en el espacio. No hay ni que decir que este triunfo totalmente imprevisto produjo sensación en el mundo matemático. Por mejor decir, inauguró un nuevo rumbo del álgebra y del Análisis en el que el gran problema era descubrir e investigar aquellas funciones en cuyos términos pudiera ser resuelta explícitamente en forma finita. la ecuación general de n grado. El mejor resultado hasta ahora obtenido es el del discípulo de Hermite, Poincaré, en el año 1880, quien creó las funciones que dan la solución requerida. Resultó ser una generalización "natural" de las funciones elípticas. La característica de las funciones era que generalizadas tenían periodicidad. Otros detalles nos llevarían demasiado lejos, pero volveremos a ocuparnos de estas cuestiones al hablar de Poincaré.
Otro de los resultados aislados sensacionales de Hermite fue el que estableció la transcendencia del número que en el Análisis matemático se representa por la letra e, o sea
donde 1! Significa 1, 2! = 1 ´ 2, 3! = 1 ´ 2 ´ 3, 4! = 1 ´ 2 ´ 3 ´ 4, y así sucesivamente; este número es la "base" del llamado "sistema natural" de logaritmos, y es aproximadamente 2.718281828... Se ha dicho que es imposible concebir un Universo en el que e y p (la razón de la circunferencia de un círculo a su diámetro) no existan. Sin embargo, lo que puede ocurrir (en la realidad es falso) es que ese encuentre por todas partes en la Matemática corriente, pura y aplicada. Del siguiente hecho puede inferirse el porqué esto es así, al menos en lo que concierne a la Matemática aplicada: e x , considerada como una función de x , es la única función de x cuya derivada respecto de x es igual a la, función misma.
El concepto de "transcendencia" es extraordinariamente simple y también extraordinariamente importante. Cualquier raíz de una ecuación algebraica cuyos coeficientes son enteros racionales (0, ±1, ±2, ...) se llama un número algebraico. Así Ö ` -1, 2.78 son números algebraicos, debido a que son raíces de las respectivas ecuaciones algebraicas x 2 + 1 = 0, 50 x - 139 = 0, en las cuales los coeficientes (1, 1, para el primero, 50, - 139 para el segundo) son enteros racionales. Un "número" que no es algebraico se llama transcendente. Diciéndolo con otras palabras, un número transcendente es aquel que no satisface una ecuación algebraica de coeficientes enteros racionales.
Ahora bien, dado un "número" constituido de acuerdo con alguna ley definida, es una cuestión muy importante preguntarse si es algebraico o transcendente. Consideremos, por ejemplo, el siguiente número simplemente definido
en el que los exponentes, 2, 6, 24, 120,... son las factoriales sucesivas, o sea 2 = 1 ´ 2, 6 = 1 ´ 2 ´ 3, 24 = 1 ´ 2 ´ 3 ´ 4, 120 = 1 ´ 2 ´ 3 ´ 4 ´ 5... y la serie indicada continúa "hasta el infinito" de acuerdo con la misma ley que para los términos dados. El siguiente término es 1 / 10 720 ; la suma de los primeros tres términos es 0.1 + 0.01 + 0.000001 = 0.110001, y puede ser demostrado que la serie define realmente algún número definido que es menor que 0.12. Este número ¿es una raíz de cualquier ecuación algebraica de coeficientes enteros racionales? La respuesta es negativa aunque probar esto sin haber sido demostrado como proceder es una prueba muy difícil que significa gran capacidad matemática. Por otra parte, el número definido por las series infinitas
es algebraico; es la raíz de 99900 x - 1 = 0, (como puede ser comprobado por los lectores que recuerden cómo se suma una progresión geométrica convergente infinita).
El primero que demostró que ciertos números son transcendentes fue Joseph Liouville (el mismo que alentó a Hermite a escribir a Jacobi) quien, en 1844, descubrió una clase muy extensa de números transcendentes, de los cuales todos aquellos de la forma
donde n es un número real mayor de 1 (el ejemplo mencionado antes corresponde a n = 10) se cuentan entre los más sencillos. Pero probablemente demostrar que un sospechoso particular, como e o p es o no transcendente es un problema más difícil que inventar toda una clase infinita de transcendentes; el matemático con capacidad inventiva, dicta, hasta cierto punto, las condiciones que han de actuar, mientras el número sospechoso es completamente dueño de la situación, y en este caso es el matemático, no el sospechoso, quien recibe las órdenes que tan sólo confusamente comprende. Así, cuando Hermite demostró, en 1873, que e es transcendente, el mundo matemático quedó asombrado ante la maravillosa sencillez de la prueba.
Desde los tiempos de Hermite se ha demostrado que muchos números (y clases de números) son transcendentes. Observaremos de pasada que probablemente se han de producir nuevas pleamares en las costas de este oscuro mar. En 1934, el joven matemático ruso Alexis Gelfond demostró que todos los números del tipo a b , donde a no es 0 ni 1 , y b es cualquier número algebraico irracional son transcendentes. Esto resuelve el séptimo de los 23 problemas matemáticos sobresalientes sobre los que David Hilbert llamó la atención de los matemáticos en el Congreso internacional de París en 1900. Obsérvese que "irracional" es necesario en el enunciado del teorema de Gelfond (si b = n/m, donde n, m son enteros racionales, entonces a b , donde a es cualquier número algebraico, es una raíz de x m - a n = 0 ), y puede demostrarse que esta ecuación es equivalente a una cuyos coeficientes son todos enteros racionales.
La victoria inesperada de Hermite sobre la obstinada e hizo suponer a los matemáticos que m podría ser sometida siguiendo un procedimiento similar. Sin embargo, por lo que se refiere a Hermite ya había hecho bastante. "No arriesgaré nada, escribía a Borchardt, para intentar demostrarla transcendencia del número p . Si otros emprenden esta empresa, nadie más feliz que yo si triunfan en ella, pero creo, mi querido amigo, que será a costa de muchos esfuerzos". Nueve arios más tarde (en 1882), Ferdinand Lindemann, de la Universidad de Munich, usando métodos muy semejantes a los seguidos por Hermite para la solución de e , demostró que p es transcendente, resolviendo así para siempre el problema de la "cuadratura del círculo". De lo que Lindemann demostró se deduce que es imposible construir con regla y compás un cuadrado cuya área sea igual a la de un círculo dado, problema que ha atormentado a generaciones de matemáticos, ya antes de la época de Euclides.
Todos los charlatanes que aun se sienten atormentados por el problema deben plantearse concisamente la forma como resolvió la cuestión Lindemann. Este autor demostró que p no es un número algebraico. Pero cualquier problema geométrico que es resoluble con la ayuda de la regla y el compás, cuando se lleva a su forma algebraica equivalente, conduce a una o más ecuaciones algebraicas con coeficientes enteros racionales, que pueden ser resueltas por sucesivas extracciones de raíces cuadradas. Como p no satisface tal ecuación, el círculo no se puede "cuadrar" con dichos instrumentos.
Si se emplean otros aparatos será fácil cuadrar el círculo. Para todos los que no sean locos de atar el problema quedó completamente muerto desde hace medio siglo. Tampoco tiene mérito en el momento actual calcular a con gran número de cifras decimales. En lugar de intentar hacer lo imposible, los místicos pueden dedicarse a con templar la siguiente útil relación entre e , p , - 1 y Ö ` -1, hasta que aparezca tan familiar para ellos como lo es el ombligo de Buda a un
swami hindu.
Quien pueda percibir este misterio intuitivamente, no necesitará cuadrar el círculo.
Después que Lindemann demostró que p es un número transcendente, el único problema importante no resuelto que atrae a los aficionados es el "último teorema de Fermat". Aquí, un hombre con verdadero genio puede tener probabilidades de triunfar. Esto no significa una invitación a todos los aficionados a inundar las redacciones de revistas matemáticas con supuestas pruebas; y a este respecto recordaremos lo que sucedió a Lindemann cuando audazmente se planteó el famoso teorema. En 1901, Lindemann publicó una memoria de 17 páginas que parecía contener la prueba tan largo tiempo buscada. Señalado el error, Lindemann, impasible, empleó la mayor parte de los siguientes siete años intentando remendar lo irremendable, y en 1907 publicó sesenta y tres páginas con la prueba alegada, pero desde el principio podía verse que existía una falta en el razonamiento. Si esto no demuestra que es preciso un talento singular para resolver la cuestión nada podrá demostrarlo.
Por grandes que sean las contribuciones de Hermite a la parte técnica de la Matemática, tiene probablemente más importancia para la cultura su tenaz argumentación de que la ciencia está más allá de las naciones, y por encima de los credos que dominan o embrutecen a la perseguida humanidad. Nos basta examinar la serena belleza de su espíritu para que lamentemos no encontrar ahora en el mundo de la ciencia algo semejante. Hasta cuando los arrogantes prusianos humillaron París en la guerra francoprusiana, Hermite, aunque era patriota, levantó su cabeza, y vio claramente que la Matemática del "enemigo" era Matemática y nada más que Matemática. Actualmente, cuando un hombre de ciencia se plantea una cuestión, no es impersonal, en su supuesta amplitud de miras, sino agresivo, como corresponde a un hombre que está a la defensiva. Para Hermite era tan obvio que el conocimiento y la sabiduría no son prerrogativas de una secta, de un credo o de una nación, que jamás se esforzó en traducir sus pensamientos en palabras. Lo que Hermite sabía por instinto lo coloca dos siglos por delante de nuestra generación. Murió, amando al mundo sobre todas las cosas, el 14 de enero de 1901.
|
|
|