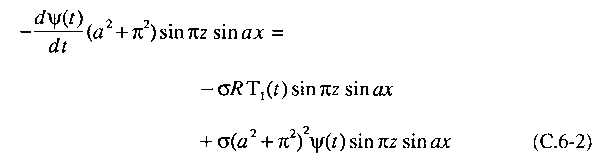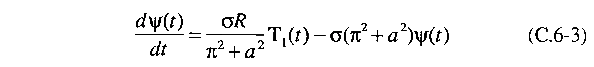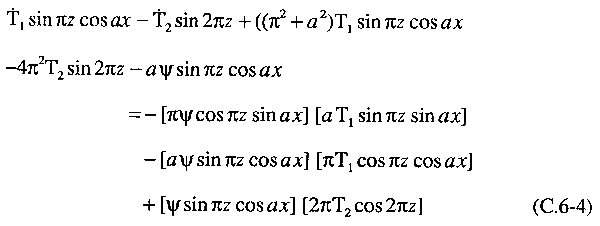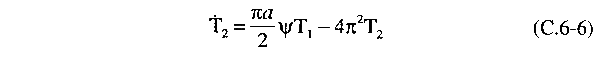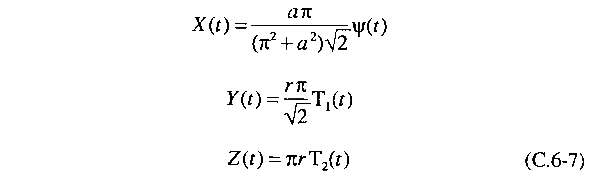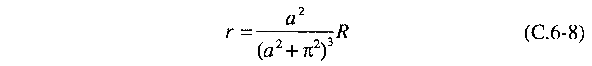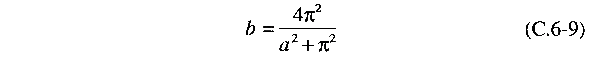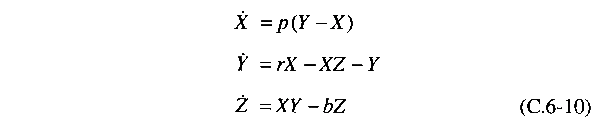Agora substituímos as formas assumidas para a função de corrente e a função de desvio de temperatura dentro das Eqs. (C.4-2) e (C.4-5). A medida que fazemos isto, encontramos que a maioria dos termos se simplifica. Por exemplo, temos    O resultado líquido é que algumas das expressões complicadas que surgem dos termos 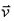.grad v desaparecem, e nós ficamos com    A única forma em que a equação original pode ser válida para todos os valores de x e z é pelos coeficientes dos termos do seno satisfazendo    A equação de desvio da temperatura é um pouco mais complicada. Ela toma a forma    Primeiro coletamos todos os termos que envolvem senπzcosax. Notamos que o último destes termos na Eq. (C.6-4) é 2aπψT₂senπzcosaxcos2πz. Usando identidades trigonométricas padrão, este termo pode ser escrito como a seguinte combinação de senos e co-senos: (-1/2senπz+1/2sen3πz)cosax. O termo sen3πz tem uma dependência espacial mais rápida do permitido pelo nosso ansatz; então, eliminamos este termo. Então devemos equacionar os coeficientes dos termos na Eq. (C.6-4) que envolvem senπzcosax para obter    Todos os outros termos na equação de desvio da temperatura são multiplicados pelos fatores sen2π . De novo, equacionando os coeficientes, encontramos    Para chegar à forma padrão das equações de Lorenz, agora fazemos umas poucas mudanças simples de variáveis. Primeiro, mudamos outra vez a variável de tempo introduzindo uma nova variável t´´ = (π² + a²)t'.
Então fazemos as seguintes substituições: onde r é o chamado número de Rayleigh reduzido: Também introduzimos um novo parâmetro b definido como    Com todas estas substituições e com a troca de σ por p para o número Prandtl, finalmente chegamos à forma padrão das equações de Lorenz: 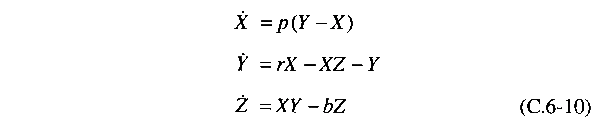   Neste ponto poderíamos fazer uma pausa para notar um importante aspecto da relação entre o modelo de Lorenz e a realidade do fluxo de fluidos. A truncagem da expansão seno-coseno significa que o modelo de Lorenz permite somente um modo espacial na direção de x com “comprimento de onda” 2π/a. Se o movimento real do fluido enfrenta uma estrutura espacial mais complexa, como ocorreria se a diferença de temperatura entre as camadas de cima e de baixo se tornasse muito grande, então as equações de Lorenz não fornecem mais um modelo útil da dinâmica.
   Observemos também onde a não-linearidade entra no modelo de Lorenz. Vemos na Eq. (C.6-10) que os termos de produto XZ e XY são os únicos termos não lineares. Estes expressam uma ligação entre o movimento do fluido (representado por X, proporcional à função de corrente) e o desvio de temperatura (representado por Y e Z, proporcionais a T₁ e T₂ , respectivamente). O modelo de Lorenz não inclui, por causa da escolha das funções do modo espacial, a não linearidade comum de 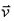grad v  da equação de Navier-Stokes.