C.5
Expansão de Fourier, Truncagem de Galerkin, e Condições Limite
English version
Obviamente,
enfrentamos uma tarefa muito difícil ao tentar resolver as equações
diferenciais parciais que descrevem nosso sistema modelo. Para as
equações diferenciais parciais, a prática comum é buscar soluções
que podem ser escritas como produtos de funções, cada uma das quais
depende somente de uma das variáveis independentes x, z,
t. Como nós temos uma geometria retangular, esperamos ser
capazes de encontrar uma solução da forma
 |
onde λs
são os comprimentos de onda dos vários modos espaciais de Fourier
e ωm,n são as freqüências correspondentes.
Nós teríamos, claro, uma equação similar para τ, a variável
de temperatura. (O Apêndice A contém uma concisa introdução à análise
de Fourier.)
Como vimos no Capítulo 11, o procedimento padrão consiste em usar
esta expansão de seno e co-seno nas equações diferenciais parciais
originais para desenvolver um grupo correspondente de equações diferenciais
ordinárias (relacionadas). Este procedimento levará a um grupo infinito
de equações diferenciais ordinárias. Para progredir, devemos, de
alguma forma, reduzir este grupo infinito para um grupo finito de
equações. Este processo de truncagem é conhecido como o procedimento
de Galerkin .
Para o modelo de Lorenz, olhamos para as condições limite que devem
ser satisfeitas pela função de corrente e a função de desvio de
temperatura e escolhemos um grupo muito limitado de termos seno
e co-seno que irão satisfazer estas condições limite. É difícil
justificar esta truncagem a priori, mas as soluções numéricas de um
grupo maior de equações parecem indicar (SAL62) que a forma reduzida
captura a maior parte da dinâmica sobre pelo menos um limitado intervalo
de valores de parâmetro.
As condições limite para a função de desvio de temperatura são
simples. Como τ representa a variação a partir do gradiente
linear de temperatura e como as temperaturas nas superfícies mais
baixa e mais alta são fixas, devemos ter
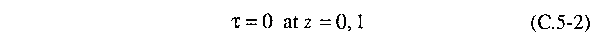 |
Para a função
de corrente, olhamos primeiro para as condições limite nos componentes
da velocidade. Assumimos que nas superfícies alta e baixa o componente
vertical da velocidade vz deve ser 0. Também assumimos
que podemos ignorar as forças de cisalhamento nas superfícies alta
e baixa. Como vimos no Capítulo 11, estas forças são proporcionais
ao gradiente do componente de velocidade tangencial; portanto, esta
condição se traduz em ter ∂vx/∂z
= 0 em z = 0 e z = 1. Para o modelo de Lorenz, estas
condições são satisfeitas pelo seguinte ansatz para a função
de corrente e a função de desvio de temperatura:
 |
onde o parâmetro
a deve ser determinado. Como veremos, esta escolha de funções
não somente satisfaz as condições limite, mas também simplifica
consideravelmente as equações resultantes.
A forma particular da parte espacial da função de corrente Ψ
modela as correntes de convecção observadas quando o fluido começa
a se mover. Você pode facilmente comprovar isto calculando os componentes
de velocidade da Eq. (C.4-1). A forma para a função de desvio de
temperatura tem duas partes. A primeira, T1, dá a diferença
de temperatura entre as partes em movimento para cima e para baixo
de uma célula convectiva. A segunda, T2, dá o desvio
a partir da variação linear de temperatura no centro de uma célula convectiva como uma função da posição vertical z. (O sinal
de menos na frente do termo T2 é escolhida de forma que
T2 é positivo: a temperatura no fluido deve ficar entre
Tw e Tc.)
|

