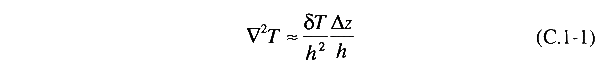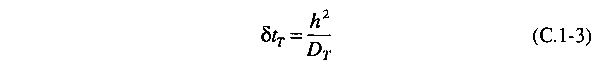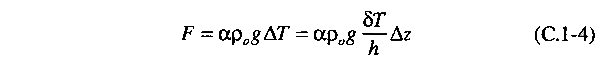Neste apêndice mostramos como as equações do modelo de Lorenz introduzidas no capítulo 1 são desenvolvidas (derivadas é uma palavra muito forte) a partir da equação de escoamento Navier-Stokes e a equação que descreve a difusão da energia térmica. Este desenvolvimento fornece um protótipo para o processo comum de encontrar equações modelo aproximadas, mas úteis, quando não podemos resolver as equações fundamentais que descrevem alguma situação física.
   O modelo de Lorenz se tornou quase totêmico no campo da dinâmica não linear. Desafortunadamente, a maioria das derivações das equações do modelo de Lorenz dizem tão pouco ao público que são essencialmente inúteis, a não ser para os especialistas em dinâmica de fluidos. Neste apêndice, esperamos dar uma descrição suficientemente completa para que os leitores deste texto cheguem a uma boa compreensão tanto do conteúdo físico quanto das aproximações matemáticas incluídas neste modelo largamente citado.
   O modelo de Lorenz descreve o movimento de um fluido nas condições da corrente de Rayleigh-Bénard: um fluido incompressível está contido numa célula que tem uma temperatura T_w mais alta na parte de baixo e uma temperatura T_c mais baixa na parte de cima. A diferença de temperatura δT = T_w - T_c é considerada como o parâmetro de controle para o sistema. A geometria é mostrada na Fig. C.1.

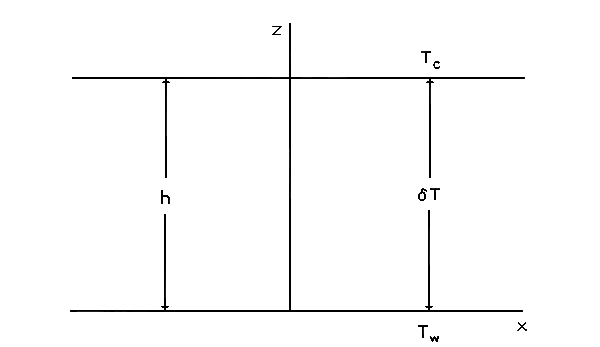Fig. C.1. Um diagrama da geometria do modelo de Lorenz. O sistema é infinito em extensão na direção horizontal e na direção para dentro e para fora da página.   Na placa de baixo z = 0.

   Antes de começar o tratamento formal da corrente de Rayleigh-Bénard, devemos desenvolver alguma intuição sobre as condições que provocam o começo da corrente de convecção. Resumidamente, quando o gradiente de temperatura entre as placas de cima e de baixo se torna suficientemente alto, uma pequena unidade de fluido que por acaso suba um pouco experimentará uma força de empuxo ascendente porque se deslocou para uma área de temperatura mais baixa e, portanto, densidade mais alta: agora é menos denso que o seu ambiente. Se a força ascendente é suficientemente forte, a unidade se deslocará para cima mais rapidamente do que sua temperatura consegue baixar. (Como a unidade está inicialmente mais quente que o ambiente, ela tenderá a liberar energia térmica para seu ambiente.). Então as correntes de convecção começarão a fluir. Por outro lado, se a força de empuxo é relativamente fraca, a temperatura da unidade cairá antes que ela possa se deslocar por uma distância significativa, e ela permanece estável na posição.
   Podemos ser levemente mais quantitativos a respeito deste comportamento usando nosso conhecimento (adquirido no Capítulo 11) sobre a difusão de energia térmica e forças viscosas em fluidos. Imagine que o fluido originalmente está em repouso. Nós queremos ver se esta condição é estável. Começamos considerando uma pequena unidade de fluido que se encontra deslocada para cima por uma pequena quantidade ∆z. A temperatura nesta área é mais baixa pela quantidade ∆T = (δT/h)∆z. De acordo com a equação de difusão térmica de energia (Capítulo 11), a taxa de mudança da temperatura é igual ao coeficiente de difusão térmica D_T multiplicado pelo Laplaciano da função da temperatura. Por este pequeno deslocamento, podemos aproximar o Laplaciano em 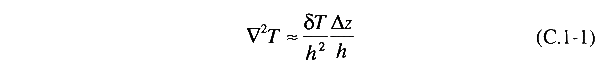   Então definimos um tempo de repouso térmico δt_T tal que onde a segunda igualdade segue da equação de difusão térmica. Usando nossa aproximação para o Laplaciano, encontramos que    Consideremos agora o efeito da força de empuxo sobre a unidade de fluido. Esta força de empuxo é proporcional à diferença na densidade entre a unidade e seu ambiente. Esta diferença em si é proporcional ao coeficiente de expansão térmica α (que dá a mudança relativa na densidade pela mudança de temperatura da unidade) e a diferença da temperatura ∆T. Assim, encontramos para a força de empuxo onde ρ_o é a densidade original do fluido e g é a aceleração devido à gravidade.
   Presumimos que esta força de empuxo equilibra a força viscosa do fluido; conseqüentemente, a unidade se desloca com uma velocidade constante v_z. Então, leva um tempo τ_d = ∆z/v_z para que a unidade se desloque através da distância ∆z. Como aprendemos no Capítulo 11, a força viscosa é igual à viscosidade do fluido multiplicada pelo Laplaciano da velocidade. Assim, aproximamos a força viscosa como onde a igualdade na extrema direita determina nossa aproximação para o Laplaciano de v_z.
   Se agora queremos que a força de empuxo seja igual em magnitude à força viscosa, encontramos que v_z pode ser expresso como O tempo de deslocamento então é dado por    O estado original de não-convectividade é estável se o tempo de difusão térmica é menor do que o correspondente tempo de deslocamento. Se o tempo de difusão térmica é mais longo, então a unidade de fluido continuará a sentir uma força ascendente, e a convecção continuará. A razão importante é a razão entre o tempo de difusão térmica e o tempo de deslocamento. Esta razão é chamada de número de Rayleigh R e toma a forma    Como veremos, o número Rayleigh é na verdade o parâmetro crítico para a convecção de Rayleigh-Bénard, mas necessitamos um cálculo mais detalhado para nos dizer o valor real do número de Rayleigh para o qual a convecção começa.