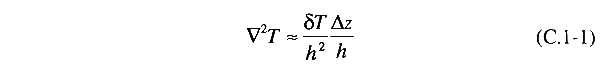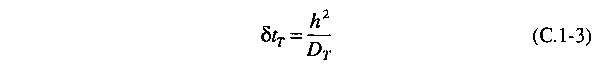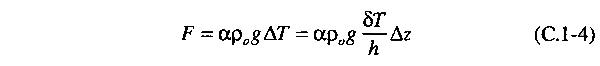Versão em Português

C.1 Introduction

In this appendix we show how the Lorenz model equations introduced in Chapter 1 are developed (derived is too strong a word) from the Navier-Stokes equation for fluid flow and the equation describing thermal energy diffusion. This development provides a prototype for the common process of finding approximate, but useful, model equations when we cannot solve the fundamental equations describing some physical situation.

The Lorenz model has become almost totemistic in the field of nonlinear dynamics. Unfortunately, most derivations of the Lorenz model equations leave so much to the reader that they are essentially useless for all but specialists in fluid dynamics. In this appendix, we hope to give a sufficiently complete account that readers of this text come away with a good understanding of both the physics content and the mathematical approximations that go into this widely cited model.

The Lorenz model describes the motion of a fluid under conditions of Rayleigh-Bénard flow: an incompressible fluid is contained in a cell which has a higher temperature T_w at the bottom and a lower temperature T_c at the top. The temperature difference δT = T_w - T_c is taken to be the control parameter for the system. The geometry is shown in Fig. C.1.

Before launching into the formal treatment of Rayleigh-Bénard flow, we should develop some intuition about the conditions that cause convective flow to begin. In rough terms, when the temperature gradient between the top and bottom plates becomes sufficiently large, a small packet of fluid that happens to move up a bit will experience a net upward buoyant force because it has moved into a region of lower temperature and hence higher density: It is now less dense than its surroundings. If the upward force is sufficient1y strong, the packet will move upward more quickly than its temperature can drop. (Since the packet is initially warmer than its surroundings, it will tend to loose thermal energy to its environment.) Then convective currents will begin to flow. On the other hand if the buoyant force is relatively weak, the temperature of the packet will drop before it can move a significant distance, and it remains stable in position.

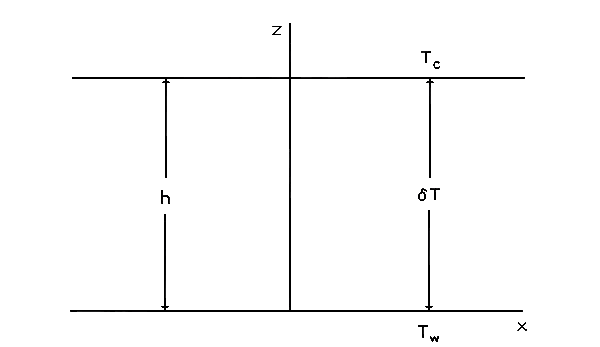Fig. C.1. A diagram of the geometry for the Lorenz model. The system is infinite in extent in the horizontal direction and in the direction in and out of the page. z = 0 at the bottom plate.

We can be slightly more quantitative about this behavior by using our knowledge (gained in Chapter 11) about thermal energy diffusion and viscous forces in fluids. Imagine that the fluid is originally at rest. We want to see if this condition is stable. We begin by considering a small packet of fluid that finds itself displaced upward by a small amount ∆z. The temperature in this new region is lower by the amount ∆T = (δT/h )∆z. According to the thermal energy diffusion equation (Chapter 11), the rate of change of temperature is equal to the thermal diffusion coefficient D_T multiplied by the Laplacian of the temperature function. For this small displacement, we may approximate the Laplacian by

We then define a thermal relaxation time δt_T such that

where the second equality follows from the thermal diffusion equation. U sing our approximation for the Laplacian, we find that

Let us now consider the effect of the buoyant force on the packet of fluid. This buoyant force is proportional to the difference in density between the packet and its surroundings. This difference itself is proportional to the thermal expansion coefficient α (which gives the relative change in density per unit temperature change) and the temperature difference ∆T. Thus, we find for the buoyant force

where ρ₀ is the original density of the fluid and g is the acceleration doe to gravity.

We assume that this buoyant force just balances the fluid viscous force; therefore, the packet moves with a constant velocity v_z. It then takes a time τ_d = ∆z/v_z for the packet to be displaced through the distance ∆z. As we learned in Chapter 11, the viscous force is equal to the viscosity of the fluid multiplied by the Laplacian of the velocity. Thus, we approximate the viscous force as

where the right-most equality states our approximation for the Laplacian of v_z.

If we now require that the buoyant force be equal in magnitude to the viscous force, we find that v_z can be expressed as

The displacement time is then given by

The original nonconvecting state is stable if the thermal diffusion time is less than the corresponding displacement time. If the thermal diffusion time is longer, then the fluid packet will continue to feel an upward force, and convection will continue. The important ratio is the ratio of the thermal diffusion time to the displacement time. This ratio is called the Rayleigh number R and takes the form

As we shall see, the Rayleigh number is indeed the critical parameter for Rayleigh-Bénard convection, but we need a more detailed calculation to tell us the actual value of the Rayleigh number at which convection begins.