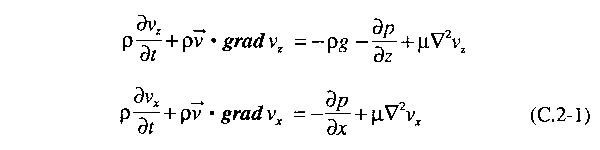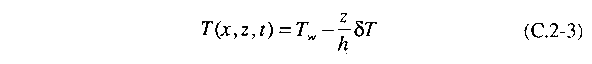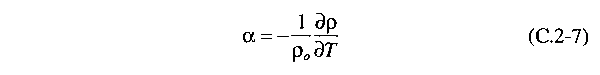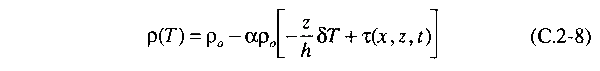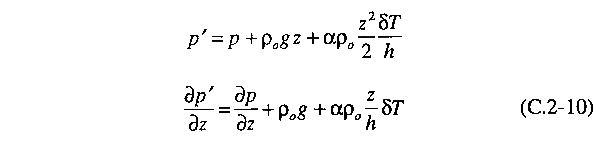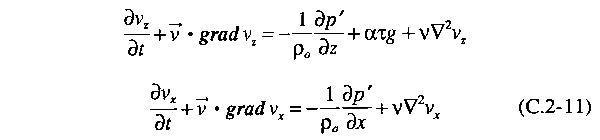Por causa da geometria assumida, o fluxo do fluido pode ser considerado bi-dimensional. Então, precisamos considerar somente os componentes x (horizontal) e z (vertical) da velocidade do fluido. As equações de Navier-Stokes (ver Capítulo 11) para os componentes  x  e  z da velocidade do fluido são Na equação (C.2-1), ρ é a densidade da massa do fluido; g é a aceleração devida à gravidade; p é a pressão do fluido, e μ é a viscosidade do fluido. Note-se que a aceleração devida à gravidade somente afeta a equação do componente z.
   A temperatura T do fluido é descrita pela equação da difusão térmica (ver Capítulo 11), que toma a forma onde, como antes, D_T é o coeficiente de difusão térmica.
   No estado não-convectivo estável (quando o fluido está sem movimento) a temperatura varia linearmente de baixo para cima: Para os propósitos de nosso cálculo, concentraremos nossa atenção numa função τ(x, z, t) que nos diz como a temperatura se desvia deste comportamento linear: Se usamos a Eq. (C.2-4) na Eq. (C.2-2), encontramos que τ satisfaz    Agora precisamos levar em consideração a variação da densidade do fluido com a temperatura. (É esta diminuição de densidade com a temperatura que leva a uma força de empuxo, que inicia a convecção do fluido.) Fazemos isto escrevendo a densidade do fluido em termos de uma expansão da série: onde ρ_o é a densidade do fluido avaliada em T_w.
   Introduzindo o coeficiente de expansão térmica α, que é definido como e usando T - T_w da Eq. (C.2-4), podemos escrever a variação de temperatura da densidade como    A densidade do fluido ρ aparece em vários termos nas equações de Navier-Stokes. A aproximação de Boussinesq, amplamente usada na dinâmica de fluidos, diz que podemos ignorar a variação da densidade em todos os termos exceto o que envolve a força devida à gravidade. Esta aproximação reduz a equação v_z na Eq. (C.2-1) para    Então reconhecemos que quando o fluido não está se movimentando, os três primeiros termos no lado direito da equação anterior devem aumentar para 0. Então, introduzimos um gradiente efetivo de pressão, que tem a propriedade de ser igual a 0 quando não existe movimento de fluido: Finalmente, usamos este gradiente efetivo de pressão nas equações de Navier-Stokes e o dividimos por ρ_o para obter

onde ν = μ/ρ_o é a chamada viscosidade cinemática.