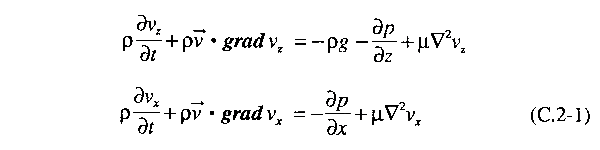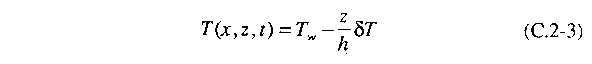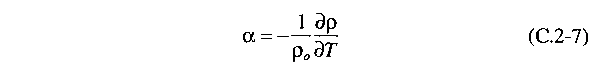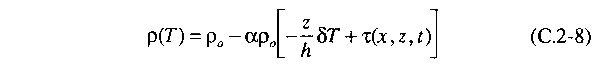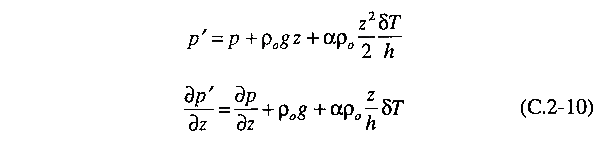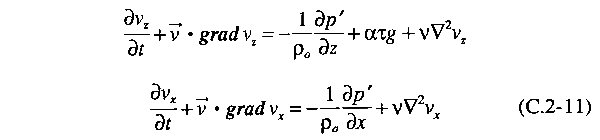C.2 The Navier-Stokes Equations

Versão em Português

Because of the geometry assumed, the fluid flow can be taken to be two dimensional. Thus, we need consider only the x (horizontal) and z (vertical) components of the fluid velocity. The Navier-Stokes equations (see Chapter 11) for the x and z components of the fluid velocity are

In Eq. (C.2-1), ρ is the mass density of the fluid; g is the acceleration due to gravity; p is the fluid pressure, and μ is the fluid viscosity. Note that the acceleration due to gravity only affects the z component equation.

The temperature T of the fluid is described by the thermal diffusion equation (see Chapter 11), which takes the form

where, as before, D_T is the thermal diffusion coefficient.

In the steady nonconvecting state (when the fluid is motionless) the temperature varies linearly from bottom to top:

For the purposes of our ca1culation, we will focus our attention on a function τ(x, z, t) that tells us how the temperature deviates from this linear behavior:

If we use Eq. (C.2-4) in Eq. (C.2-2), we find that τ satisfies

We now need to take into account the variation of the fluid density with temperature. (It is this decrease of density with temperature that leads to a buoyant force, which initiates fluid convection.) We do this by writing the fluid density in terms of a power series expansion:

where ρ₀ is the fluid density evaluated at T_w.

Introducing the thermal expansion coefficient α, which is defined as

and using T- T_w from Eq. (C.2-4), we may write the density temperature variation as

The fluid density p appears in several terms in the Navier-Stokes equations. The Boussinesq approximation, widely used in fluid dynamics, says that we may ignore the density variation in all the terms except the one that involves the force due to gravity. This approximation reduces the v_z equation in Eq. (C.2-1) to

We then recognize that when the fluid is not convecting, the first three terms on the right-hand side of the previous equation must add to 0. Hence, we introduce an effective pressure gradient, which has the property of being equal to 0 when no fluid motion is present:

Finally, we use this effective pressure gradient in the Navier-Stokes equations and divide through by ρ₀ to obtain

where v = μ/ρ₀ is the so-called kinematic viscosity.