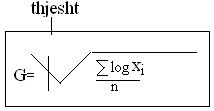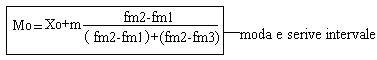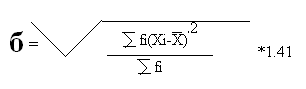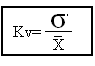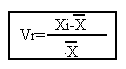KAPITULLI 4

4.ANALIZA STATISTIKORE

 

Analiza statistikore paraqet fazen e tret dhe te fundit te studimi te dukurise massive. Kjo faze pason pas hulumtimeve te bera rreth vrojtimit, permbledhjes, grupimit dhe paraqitjes grafike te te dhenave te sistemuara. Permes analizes arrihet rezultati I cili shpreh qarte ndikimin e faktoreve te llojllojshem ne ecurin e dukuris massive.

Permesa analizs statistkore arrihet disa tregues te dnryshem permes te cileve nxirren konkuldime per dukurin e studiuar. Analiza rendesi ka zakonsihst ne karahsimin e te dhenave dhe rezultateve per dy e me shum dukurive ne kohe dhe hapsire.

Analiza statike statistikore mbeshtetet ne perpunimin e te dhenave no momentin e caktuar, psh perpunimin e te dhenave gjate anketave, regjstrimeve ETJ.

Analiza dinamike palikohet kur dukuria permabn tipare kohore dhe hapsinore.

Analiza representative-aplikohet ne analizen e nje pejese te dukruis dhe dhenjes se karakteristikave te pergjitshme te teresis permes analizes se nje pejese te teresis se pergjithsme.

Analiza regressive-hulumton raportet dhe lidhshmerit reciproke ne mes te dukruive te ndryshme massive.

 

3.1.MADHESIT MESATARE STATISTKORE

 

pra nga fazat paraprake te studimit statistkore krijohen serite te cilat shprehen si madhesi absolute dhe relative. Shmangjest krahasimet jane te lehta te mirren vesh nese kemi te bejm me seri qe ka numer te vogel te modalitetve, mirepo te serite qe kane numer te madh te modaliteteve duhet qe te mirret nje madhesi qe e prezenton ate seri statstikore. Pra kjo madhesi do te perfaqson te gjitah te dhenat ne serin e analizuar.

Duhet cekur se madhesia mesataremund te llogarite vetem te serite sasiore te nejsive statsitkore. Madhesit mesatarene serin e te dhenave te nejsis statstikore, gjenden gjithmon ne mes te modalitetit me te vogel dhe modalitetit me te madh te asaj serie. Permes mesatareve shprehen shume tregues te rendesishem te gjendjes, ecuris dhe zhvillimit te dukurive te ndryshme. Zbatimi I mesatareve varet edhe nga natyra e te dhenave dhe qellimi I studimit. Mirpo per analizen e serive statistikoreme kryesoret jane: mesatarja aritemtike, harmonike dhe gjeometrike, ndryshe keto mesatare quhen edhe algjebrike sepse llogariten me formula matematikore. Pos ketij grupi te mesatareve kemi edhe grup tjeter qe hulumton poziten e modalitit ne serin statistikore dhe quhen mesatare te pozicionit. Keto jane moda, mesorja dhe kuartilet.

 

MADHESIT MESATARE ALGJEBRIKE

 

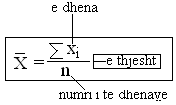
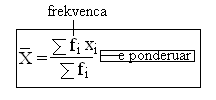
Mesatarja aritmetike(x)- ne analizen e dukurive massive me se shumti perdoret  kjo mesatare. Perdorim me cilsor kane te serite homogjene, te njeisve statsitkore ndersa ne rastet e tjera kemi rezultat te gabuar. Dhe varesisht nga modalitete e tipareve te njesive statsitsikore dallojme mesatare aritemtike te thejsht dhe te ponderuar. Nese te dhenat paraqiten vetem nga nje here perdorim mesataren aritemteike te thjesht dhe e kunderta. Mesatarja aritmetike e ndonje serie paraqet perfaqsuesin e asaj serie dhe paraqet madhsin mesatare te asaj serie.

                      

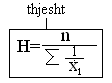
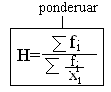
 Mesatarja harmonike(H)-si metode e llogaritjes se madhsis mesatare te tiparit te dukuris se analziuar, perdoren ne rastet kur mesatarja aritemtike nuk jep rezultate te sakta. Andaj H definohet si vler reciporkkee mesatares aritemtike. Pra kjo mesatare rrjedh nga mesatarja aritemtike. Edhe msataraja harmonike varesisht se si paraqiten variacionet kemi te thjesht dhe te ponderuar me frekuenca. Gjithashtu vlera e fituar na paraqet mesataren e asaj serie ose te thejesht ose te ponderuar.

                                                    

 

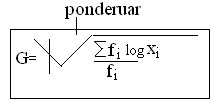
Mesatarja Gjeomterike(G)- ben pjese ne madhesit mesatare algjebrike e cila ne statistike perdoret per llogaritjen e nomres mesatare te zhvillimit te dukruis ne periudha te dnryshme. Pra kjo perdoret kur serite stastistkore posedojne veqorin e regresionit dhe e e llogarisim se qfar norme te zhvillimi ka ajo dukuri. Gjithashtu edhe te kjo mesatare ne varshmeri nga modalitetet kemi mesatare gjeomettirke te thjesht dhe te ponderuar.

                    

Per gjetjen e norms mesatare te zhvillimi te nje dukurie duhet qe te aplikohen koeficientet zingjir qe paraqesin raportin ne mes te madhesis raportuse dhe asaj paraprake pra N2/N1-paraqet k1 koeficientin e pare zingjiror keshtu veprojm deri ne fund….

 

MADHESIT MESATARE TE POZICIONIT

       

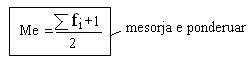
Pos mesatareve algjebrike kemi edhe mesataret e pozicionit ku bejn pjes mesorja, moda, kuartili. Quhet et pozicinoit sepse gjate gjetejes se tyre merret parasysh pozita e tyre ne serin statsitskore. Rradhitja e modaliteteve ne seri sipas madhesive I paraprin llogartijes se mesatareve te pozicionit.

  Mesorja- paraqet modalitetin e tiparit I cili ndodhet ne mes te series statistikore, pra mediana e ndan serine ne dy pjese te barabarta mbi vleren e medians madhesit jane me te vogla dhe ner medianen jane me te medhaja. Duke u nisur nga lloji I serive dallojme mesore te thejsht dhe te ponderuar.

                          

Dhe dallojme mesore te serive me intervale ku formula e saj eshte keshtu:

 

Moda(Mo)- paraqet vleren e modalitetit me pjesmarrje me te madhe ne seri, pra me frekuence me te madhe ne seri. Moda pra percaktohet vetem ne seri qe kane frekuence. Varesisht nga madheisa e numrit te frekuencave seria mund te jet unimodale, bimodale dhe multimodale.

Edhe moda dallon ne seri jointervae dhe ne seri intervale. Tek seria jo intervale vetem e shiqojme frekuencen me te madhe dhe e gjeme moden, ndersa te serit jo intervale duhet te perdorim kete formul. Kur ta gjejm vlerenm e modes mund te konludojme se ai modalitet ka qene me ne MODE, ka pase me frekuence me te madhe se variantat tjere.

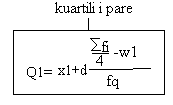
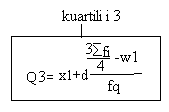
Kuartilet(Q)-kuartilet jane madheis qe shume e frekuencave te modaliteteve te tiparit e ndajne ne kater pjese te barabarta. Me kryesore jane kuartili I ulet Q1 dhe kuartili I larte Q2. kuartili I pare e paraqet ¼ te modaliteteve ndersa Q3 perebet nga ¾ e modaliteteve te series statistikore. Edhe kuartilet llogariten njejt si mesorja me ane te rangut te kuartilit se pari per ta gjetur se ku gjindet kuartili dhe pastaj me ane te formules I zavendesojm vlerat dhe gjeme kuartilin.

                                

 

TREGUESIT E VARIACIONIT

 

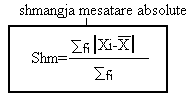
Variacioni shprehet permes treguesve te cilet paraqesin nivelin e shmangieve te modaliteteve nga madhesia mesatare e serive te analizuara. Pra tregeusit e variacionit jane te lidhur ngushte me mesataren artimetike te serive stastitskiore. Ato tregeus percaktojne masen e shmangjes se modaliteteve nga mesatarja artimetike e tyre ne menyre sasiore me vlera numerieke pra. Matja e shmangieve beher permes tregeusve relative dhe absolute te varicionit.

Tregeusit absolut te variacionit

Perems tyre hulumtohen se a ka dallime mes modaliteteve dhe sa eshte I madh ai dallim nga mesatarja e asaj serie. Tregeusit absolute shprehen permes njesive konkrete matese si KG, TON, LITER etj dhe gjithmon jane te njejta me njesit e te dhenave te cilat analizohen. Permes ketyre tregeusve maten variacionet e modaliteteve nga mesatarja aritemtike e tyre dhe ata tregeus jane:

Gjersia e variacionit- shpreh nivelin e variacionoit dhe llogaritja e saj behet duke zbritur nga modaliteti me I madh modalitetin me te vogel.  GjV=Xmax-Xmin

Shmangja mesatare absolute(Shm)- paraqet shamngien absolute te te dhenave nga mesatarja e tyre, veq duhet ti fusim ne vlera absolute.

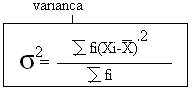
Shmangja mesatare kuadratike(varianca)- paraqet madhesin mesatare te shmangieve te te dhenva ne katror nga mesatarja aritmetike. Shenohet me shenjen greke (sigma ne katror)σ. Dhe llogarite varesisht nga serite, nese jane serite e thejshta ose te ponderuara kemi formula te ndryshsme per llogartijen e variances qe e ka vleren matese sit e te dhenave dhe shpreh se sa eshte shmangia e modaliteteve ne katror nga mesatarja e tyre.

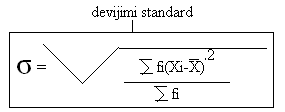
Devijimi standard (σ)- pas variances si tregues tjeter I shmangieve te modaliteteve nga mesataarja e tyre aritmetike eshte devijimi standard, qe gjithashtu kur te gjindet shpreh shmangien mesatare e te dhenave nga mesatarja e tyre aritmetike dhe eshte madhesi absolute qe shprehet me KG, ose TON ose T/p ETJ. Gjithashtu llogaritja e saj behet ne varshmeri nga serite statistikore se a jane te thjeshta apo te ponderuara.

 

Dispersioni(б)- net e vertet eshte devijimi standard I shumezuar me rrenjen katrore te dyshit, I cili shpreh shperdarjen e te dhenave perrth mesatares se tyre aritmetike, dhe llogarite me formulen e njenjt sit e devijimit standard vetem se shumezohet me 1.41

 

Tregeusit relativ te variacionit

Treguesit relative te variacionit shprehin dukurine ne perqindje ose si koeficient. Dhe tregeusit me kryesor jane:

Koeficienti I variances (Kv)- ky tregues I variacionit shpreh  madhesin relative te raportit te devijimit standard dhe mesatares aritmetike te asaj serie. Dhe ketu verejme se madhesia e koeficientit ose vleres ne perqindje varet nga madhesia e devijimit standard dhe rezultati I fituar psh 42% na tregon se te dhenat nga mesatarja aritmetike mesatarisht shmangen per 42%.

Koeficienti I dispersionit(Kd)- edhe Kd njejt si edhe ai I pirsonit apo I variances eshte tregues relative I cili ne perqindje ose ne forme te koeficientit tregon se sa psh 42% kemi shtrirje te te dhenave perreth mesatares aritmetike te tyre.

Varianca relative(Vr)- tregues me rendesi te madhe per matjen e variacionit. Paraqet shmangjen ne veqanti per qdo te dhene nga mesatarja e tyre ne raport me mesataren e tyre. Edhe variance relative mund te shprehet si koeficient edhe si perqiondje.

Interkuartili(kQ)- diferenca ne mes te kuartilit te lart dhe te ulet na paraqet interkuartilin.

kQ=Q3-Q1/Q3+Q1. dhe shprehet me vler te njejt matse si te dhenat e series.