Aula 5 - Dimensão Fractal

Aula5.zip

Para refletir:            

O que é Fractal? Que relação existe entre Caos e Fractais? Qual seria a dimensão de uma linha infinita, sem sobreposição, no interior de um sólido de volume finito? Seria possível analisar  um conjunto de dados experimentais sem conhecer o sistema de equações que descrevem o comportamento do experimento?

Teoria:

Em geral a dimensão de uma figura geométrica é dada por um número inteiro, como nos seguintes exemplos: uma linha reta tem dimensão igual a 1; um plano, dimensão igual a 2 e um sólido, dimensão 3. No entanto, existem situações em que a dimensão se torna fracionária, como por exemplo: uma linha com várias mudanças de direção, um plano ou um sólido com “buracos”, um plano com protuberâncias em outras direções, etc....

Benoit Mandelbrot levantou a possibilidade de se definir valores fracionários à dimensão analisando o contorno de um litoral. Percebeu que, dependendo do tamanho da unidade de medida adotado, o comprimento do litoral sofria variações: quanto menor a unidade adotada, maior o valor do comprimento. Levando este processo ao extremo, no limite em que a unidade de medida tende a zero, o comprimento tende a infinito. Este problema o levou à uma outra forma de medir a dimensão de uma figura geométrica, a dimensão fractal. Os objetos com dimensão fractal passaram a ser chamados de fractais.

Os atratores estranhos formam figuras com dimensão fractal no espaço de fase. A trajetória do sistema nunca se repete e nunca se cruza, percorrendo um comprimento infinito, porém, ocupando uma região limitada. Por essas características, a dimensão do atrator fornece indicações sobre o comportamento do sistema: um atrator com dimensão fractal será, muito provavelmente, um atrator estranho, o comportamento do sistema será, muito provavelmente, caótico.

Dedução matemática:

Existem diversas formas de definir dimensão fractal. Uma delas é a dimensão de capacidade, ou dimensão de Hausdorff- Besicovitch , desenvolvida pelos matemáticos alemães Felix Hausdorff (1868 - 1942) e Abram Samoilovitch Besicovitch (1891-1970), que discutiremos a seguir.

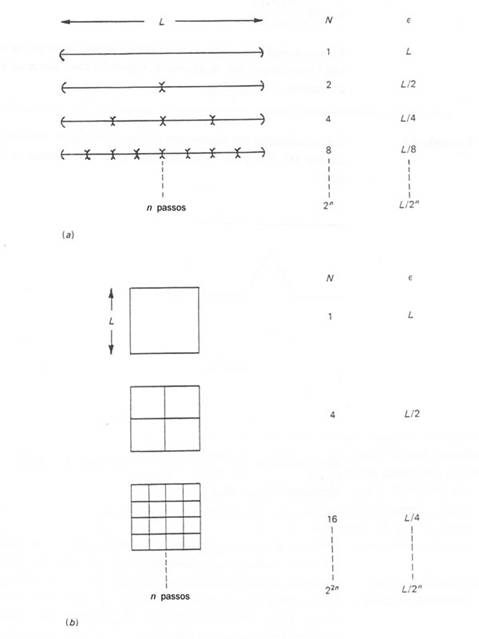Figura 8 - Aplicação do método das caixas para calcular a dimensão de capacidade. Em (a) para um segmento de reta, em (b) para um quadrado.

Se uma linha de comprimento L for partida em segmentos iguais, de tamanho ε como na Figura 8(a), quanto maior o número de segmentos N(ε), menor será o tamanho de ε, de tal forma que:

No caso de um quadrado de lado L, como na Figura 8(b), temos:

Generalizando, teremos:

Tomando-se o logaritmo dessa expressão:

Considerando que o termo em L será desprezível para pequenos valores de ε, a dimensão de capacidade pode ser definida pela expressão:

onde ε é o tamanho da aresta (lado ou comprimento) da caixa e N(ε) é o número de caixas preenchidas.

Um exemplo de dimensão fracionária menor que a unidade é o Conjunto de Cantor (Figura 9).

Figura 9 -  Conjunto de Cantor. Dimensão de capacidade: dc = 0,63

Aplicando-se a definição acima, temos N(ε) = 2 e ε = 1/3: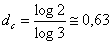

Já para a Curva de Koch (Figura 10) teremos uma dimensão maior que um, porém, menor que dois.

Figura 10 - Curva de Koch. Dimensão de capacidade: dc =1,26.

Nesse caso N(ε) = 4 e ε = 1/3:

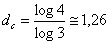Prática:

Cálculo da dimensão fractal do mapa logístico utilizando o programa dimensao.f

Figura 11 - Cálculo da dimensão fractal do atrator do mapa logístico para μ = 3,6. O coeficiente angular da reta nos dá a dimensão: dc = 0,94206.

N(ε) é o número de caixas visitadas por pelo menos um ponto do mapa.

Conclusão:

Para µ = 3,6 o atrator tem dimensão fractal diferente de 1 (Figura 11). Neste caso, ocorre o comportamento caótico.

Internet:

Texto sobre fractais:

../fractais/ 

Applet demonstrando a semelhança de escala, característica dos fractais: