LIGAÇÕES DOS FRACTAIS COM OS SISTEMAS CAÓTICOS E COMPLEXOS
Vimos
que muitos fractais são provenientes de operações não-lineares.
Existe, portanto, uma relação bastante íntima entre eles e
os sistemas dinâmicos não-lineares; estes sistemas apresentam,
em geral, comportamentos caóticos e complexos. Mencionaremos,
de forma superficial, alguns desses pontos de interface, muitos
dos quais ainda não estão claramente entendidos e são pontos
atuais de intensa pesquisa.
Dimensão
fractal de atratores
Uma
importante caracterização dos atratores caóticos é fornecida
pela sua dimensão fractal (ou, mais precisamente, pelo seu
espectro de dimensões). Um exemplo é o cômputo da capacidade
do Atrator de Lorenz, um modelo paradigmático de atrator caótico;
seu valor é de aproximadamente 2,1. Essa dimensão permite
quantificar o grau de ocupação com que o atrator preenche
o espaço de três dimensões e mostra que ele não pode estar
contido em uma superfície.
Bacias
fractais
Um
fenômeno muitas vezes existente nos sistemas caóticos e complexos,
e que tem significativas repercussões em processos evolutivos,
é a existência de atratores múltiplos, ou seja, o sistema
possui vários atratores para os mesmos valores dos parâmetros.
As condições iniciais determinarão para qual atrator o sistema
tenderá. Uma situação relativamente comum é aquela em que
as fronteiras dessas bacias de atração são fractais. Pode
ocorrer também que as próprias bacias se tomem extremamente
entrelaçadas e sejam elas mesmas estruturas fractais. Isso
tem implicações profundas na previsibilidade do comportamento
futuro do sistema, quando se tenta prever para qual atrator
ele convergirá ao longo do tempo: se as bacias foram muito
entrelaçadas, tal previsão ficará bastante limitada.
Mesmo mapas unidimensionais simples podem apresentar bacias
fractais[16].
Um exemplo bidimensional interessante ocorre no chamado mapa
do triângulo: trata-se de um mapeamento não-linear
no plano, analisado por Yorke e seus colegas[17],
no qual existem seis atratores em competição (que, neste caso,
são determinados segmentos de reta) e com bacias muito entrelaçadas.
A Figura 36 mostra as bacias de atração para cada um dos atratores.
Note-se que essas figuras não são interessantes apenas por
seu aspecto estético.
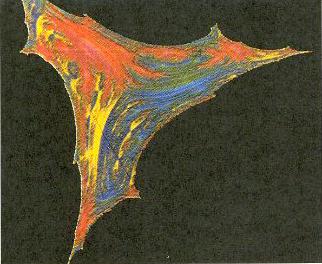 |
| FIGURA
36 – Bacias fractais do mapa do triângulo |
As
cores e sua distribuição carregam informações sobre toda a
dinâmica do sistema. Tais figuras constituem-se em uma generalização
dos gráficos tradicionais, em que a informação está contida
apenas na curva (linha unidimensional) do gráfico de uma variável
em função de outra. Já nessas figuras toda a área do papel
é importante, pois condensa, em cada ponto, informações sobre
o sistema (Figura 37).
 |
FIGURA
37 – Trajetórias de períodos diferentes para um pêndulo
forçado.
[Grupo de Caos – Universidade de Maryland] |
Conjuntos
de Julia e de Mandelbrot
Estruturas
matemáticas interessantes emergiram do estudo do comportamento
dos mapeamentos quando se usam números complexos. O exemplo
mais importante surgiu com os chamados Conjuntos de Julia
e com o Conjunto de Mandelbrot, uma figura muito bonita e
dotada de grande riqueza matemática. Vamos apenas descrever
como podem ser construídos; o livro de Peitgen e Richter[2]
pode ser consultado para maiores detalhes.
Vamos considerar uma iteração quadrática no plano complexo,
com a forma Zi+1 = Zi2 +
C, ou seja:
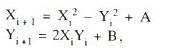 |
(5) |
onde
C = A + iB e Z = X + iY. Quando partimos de um determinado
ponto inicial e fazemos o computador calcular os pontos seguintes,
através da iteração (5), o ponto tenderá, em geral, para zero
ou para infinito.
Conjuntos
de Julia. São os conjuntos constituídos pelos pontos que
não tendem nem para zero nem para o infinito. A dinâmica dentro
deles é caótica. São obtidos fazendo-se o ponto inicial Z0
fixo e variando-se C. Uma maneira para determinar um conjunto
desse tipo é a seguinte: desenham-se todos os pontos que,
sob iteração, não escapam para infinito. A fronteira desse
conjunto é um Conjunto de Julia (Figura 38).
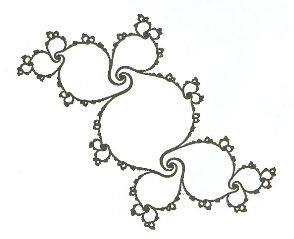 |
| FIGURA
38 – Conjunto de Julia |
Conjunto
de Mandelbrot. Nesse
caso tomamos C fixo e variamos Z0. O Conjunto de
Mandelbrot (Figura 39) é o conjunto de pontos Z0,
no plano complexo, para os quais os Zi sucessivos
não tendem para infinito. Para determiná-lo, podemos proceder
da seguinte maneira: para C = 0, por exemplo, faz-se a iteração
(5), para cada Z0 e coloca-se cor branca nos pontos
em que Z tende para infinito e preta se isto não ocorre. A
fronteira do Conjunto de Mandelbrot tem dimensão fractal igual
a 2.
O conjunto pode receber também uma estrutura a cores, que
contém informações sobre a rapidez com que os pontos tendem
para infinito. As cores diferentes são atribuídas aos pontos
iniciais de acordo com o número de iterações necessárias para
se atingir um certo raio grande, anteriormente definido. O
Conjunto de Mandelbrot é um tipo de "dicionário"
dos Conjuntos de Julia.
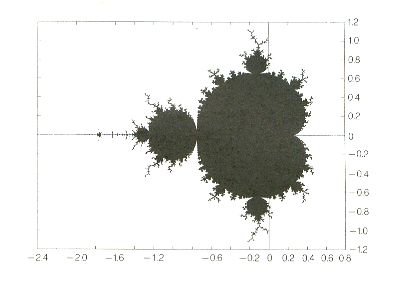 |
| FIGURA
39 - Conjunto de Mandelbrot |
Os
pontos que pertencem ao Conjunto de Mandelbrot geram conjuntos
de Julia conexos. Os pontos fora dele geram Conjuntos de Julia
(fractais) constituídos de pontos isolados. Com iterações
similares às de Mandelbrot, no plano complexo, muitas figuras
bizarras podem ser construídas, lembrando estruturas naturais
com forma de insetos, plantas, paisagens, etc. (Figura 40).
 |
| FIGURA
40 - Imagem fractal tridimensional |
Outras
questões significativas
Muitos
temas novos de pesquisa na física e na matemática têm utilizado
os conceitos da geometria fractal. Do ponto de vista matemático,
menciono apenas dois exemplos. No primeiro deles, no estudo
da integrabilidade, verifica-se que as singularidades móveis
(que aparecem quando equações diferenciais não-lineares são
analisadas no plano complexo) de sistemas de equações diferenciais
que são não-integráveis apresentam, com freqüência, uma distribuição
complicada no plano complexo; existe a conjectura de que essas
distribuições são fractais[18].
Um outro ponto matemático, recentemente estudado, diz respeito
às relações entre a geometria fractal e a teoria clássica
da computação. Existem aí problemas da categoria dos indecidíveis,
como, por exemplo, testar se um atrator de um IFS e um dado
segmento de linha se interceptam[19].
Isso significa que não existem algoritmos que possam responder
a certas questões simples sobre fractais.
Com a introdução e o uso dos fractais na física, inúmeras
questões e aplicações novas têm surgido, entre elas as que
buscam estabelecer conexões entre a estrutura fractal e o
comportamento dinâmico de sistemas caóticos e complexos. Citemos
três questões particularmente importantes:
1.
A construção de modelos adequados para se descrever a turbulência
é um dos grandes problemas da física; embora um avanço significativo
tenha sido conseguido com as novas técnicas experimentais
e com a introdução de muitos conceitos provenientes do estudo
dos sistemas caóticos, o problema parece ainda longe de uma
solução geral aceitável. Como outras equações básicas da física,
as equações dos fluidos, como as de Euler,por exemplo, podem
exibir simetria de escala. Além disso, os fluxos turbulentos
devem ser tratados estatisticamente e seus espectros apresentam
freqüentemente estrutura fractal Existe a conjectura de Mandelbrot
de que as soluções das equações básicas da turbulência envolveriam
singularidades que são conjuntos fractais [1(b)].
2.
Outra questão bastante discutida nos últimos tempos, e ainda
sem uma resposta definitiva, se refere à relação entre os
fractais e os ruídos chamados de ruídos l/fα,
que apresentam uma lei de potência na sua distribuição espectral
(em geral, 0,5 < a < 1,5). Por exemplo, um corte
ao longo de uma direção de uma paisagem fractal produz a curva
de um gráfico com ruído l/fα. Uma distribuição
desse tipo reflete a presença da simetria de escala e a toma,
em princípio, aplicável a fenômenos que não possuem comprimento
característico[20].
Os fenômenos críticos são também associados com fractais e
caos e o conceito de criticalidade auto-organizada foi
introduzido para tentar entender os sistemas que tendem naturalmente
para uma situação crítica[21].
No estado crítico não há uma escala natural de comprimento
e a estatística fractal se aplica. Os sistemas complexos existem
no limiar do caos, onde situações críticas ocorrem e a lei
de potência predomina. Muitos modelos que obedecem à lei de
potência têm sido construídos e estudados: terremotos, avalanches,
freqüência no uso de palavras, atividade solar, inversões
no campo magnético da Terra, ruídos em circuitos eletrônicos,
etc[20]. Uma
questão cabível é: existe algum mecanismo universal para gerar
ruídos desse tipo? Um possível mecanismo é o da criticalidade
auto-organizada. Os fractais e o ruído l/fα
a seriam, segundo a conjectura, as marcas espacial e temporal
da criticalidade auto-organizada[21].
É mais provável; no entanto, que vários mecanismos genéricos
existam e conduzam a esses fenômenos possuidores de simetria
de escala. Mas as questões gerais sobre qual o significado
da lei de potência e sua relação com os fractais, por que
muitas formas naturais têm estrutura fractal e por que o ruído
l/fα é prevalente em muitos processos dinâmicos
da natureza, permanecem questões substantivas que aguardam
respostas mais precisas.
3.
Uma terceira área interessante de aplicação dos fractais se
refere à construção de urna termodinâmica dos multifractais[22].
Em particular, existem interfaces entre esse estudo e as chamadas
wavelets (que fornecem um tipo de generalização da
análise de Fourier). Inspirado também na definição de dimensão
fractal generalizada, Tsallis introduziu, em 1988[23],
uma definição mais geral de entropia, que poderá ser útil
em determinados contextos físicos. Nessa seqüência de idéias,
a definição do expoente de Lyapounov também pode ser estendida
para permitir a análise da taxa média de afastamento (ou aproximação)
de trajetórias vizinhas, mesmo nos casos em que o expoente
usual de Lyapounov é nulo. Isso significará que essa taxa
não é exponencial e obedece a uma lei de potência, como ocorre
no limiar do caos, com os sistemas complexos. Estruturas fractais,
já presentes no cômputo dos expoentes usuais, poderão surgir
também aqui.
Como iniciei o texto com Langevin, terminarei, após este sobrevôo
ligeiro sobre conceitos matemáticos e físicos referentes aos
fractais, com uma frase também instigante de Spinoza: "Não
atribuo à natureza nem beleza nem deformidade, nem ordem nem
confusão; é somente do ponto de vista de nossa imaginação
que dizemos que as coisas são bonitas ou feias, ordenadas
ou caóticas".
Quando nos deparamos com o caráter estranho e abstrato de
muitas das novas idéias, como, por exemplo a da existência
de dimensões fracionárias, considerações como as de Langevin
e de Spinoza podem nos inspirar ou, até mesmo, consolar.
--------------------------------------------------------------------------------------------------------------------------------- |




