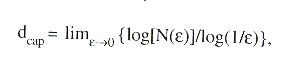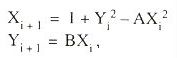| O
QUE SÃO E COMO MEDIR AS DIMENSÕES FRACTAIS?
A
noção de dimensão é uma questão fundamental tanto na matemática
quanto na física. Vamos discuti-Ia de um modo superficial,
mas que nos ajude a entender a idéia de dimensão fractal.
Duas idéias próximas, mas diversas, estão ligadas ao termo
dimensão usualmente empregado: 1) o número de informações
(no caso, dadas pelas coordenadas) necessárias para se localizar
um ponto no espaço: falamos que o espaço possui três dimensões.
Após a teoria da relatividade, a idéia de um espaço quadridimensional
se firmou na física, com a introdução também da dimensão temporal
para a caracterização de um evento que ocorre no espaço-tempo;
2) a noção de medida de comprimento. Assim, dizemos, por exemplo,
que a dimensão de um objeto é 50cm.
Uma noção importante de dimensão, a chamada dimensão topológica,
relacionada à primeira idéia, foi discutida por Poincaré
em 1911 e por Brouwer, em 1913. Diz o seguinte: um contínuo
tem n dimensões quando podemos dividi-lo por meio de cortes
que sejam eles próprios contínuos de (n-1) dimensões. Considera-se
que o ponto possui dimensão zero. Por essa definição, a reta
terá dimensão 1 (porque pode ser separada por um ponto), o
plano terá dimensão 2 (porque pode ser separado por uma reta),
o espaço usual terá três dimensões (porque pode ser separado
por um plano: as paredes de uma casa, por exemplo), e assim,
sucessivamente, podemos imaginar conjuntos contínuos com um
número crescente de dimensões. Note-se que, nessa definição,
não entra a noção de medida de distância (métrica), que, como
dissemos, aparece também associada ao termo dimensão. Trata-se
aqui de uma noção topológica, relacionada apenas à noção de
vizinhança (proximidade) entre os pontos de um conjunto, o
que permite a definição de continuidade.
Vamos considerar agora o aspecto métrico ligado à noção de
dimensão. Neste século surgiram várias noções de dimensão,
às vezes não-equivalentes, baseadas nessa característica.
A primeira delas é a denominada capacidade, definida
por Kolmogorov, que mede o quanto o conjunto ou objeto considerado
preenche o espaço em que está imerso. Por ser, talvez, a definição
de dimensão mais simples que permite caracterizar os fractais,
é usualmente chamada de dimensão fractal, embora existam,
como veremos, vários outros tipos de dimensões métricas utilizadas
para caracterizar os graus de 'fractalidade' de um conjunto.
Essa definição de capacidade é bastante próxima da noção de
dimensão introduzida por Hausdorff, em 1919.
A definição da capacidade
dcap de
um conjunto é a seguinte:
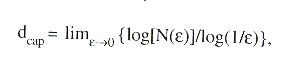 |
(1) |
onde
N(ε) é o número
mínimo de cubos elementares necessários para cobrir o conjunto
considerado e ε é a dimensão linear do cubo elementar.
Vamos considerar dois exemplos simples que mostram como essa
dimensão pode ser calculada:
1. Conjunto de Cantor. É um conjunto construído da
seguinte maneira: tomamos um segmento de reta e o partimos
em três segmentos iguais. Em seguida, o pedaço intermediário
é retirado. Os dois segmentos restantes são de novo repartidos
em três segmentos iguais e os segmentos intermediários são
retirados. O processo de repartir os segmentos e de retirar
o pedaço intermediário prossegue ad infinitum. O Conjunto
de Cantor é o conjunto de pontos restantes, após infinitas
operações terem sido realizadas.
A capacidade, ou dimensão fractal, desse conjunto, como pode
ser inferido diretamente da Figura 25, vale: dcap
= log(2)/log(3) ≈ 0,6. Isto porque, em cada etapa do
processo de construção do conjunto, utilizamos dois segmentos
(cubos elementares) para cobrir a figura, sendo que cada segmento
elementar tinha comprimento de 1/3. Observe-se que esse conjunto
tem comprimento zero, porque, a cada etapa do processo, seu
comprimento é reduzido por um fator 2/3. Logo, seu comprimento,
no limite em que n → ∞, será L = (2/3)n →
0.
 |
| FIGURA
25 - Processo de formação do Conjunto de Cantor |
2.
Conjunto de Koch: Este conjunto é construído como indicado
na Figura 26. Em vez de retirarmos o pedaço intermediário
do segmento inicial, nós o substituímos por mais dois segmentos
iguais, como indicado. Percebe-se logo que a dimensão fractal
desse conjunto será dada por dcap= log(4)/log(3)
≈ 1,26. O comprimento desse conjunto tende para infinito,
valendo em cada etapa do processo de construção (4/3)n.
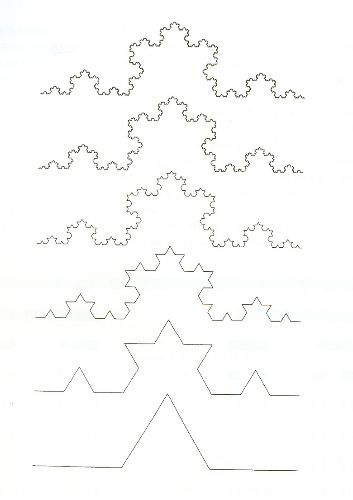 |
| FIGURA
26 - Processo de formação do Conjunto de Koch |
Muitos
outros conjuntos fractais similares podem ser imaginados com
regras de construção semelhantes. O leitor poderá facilmente
se convencer, pelo uso da definição (1), que a dimensão fractal
de uma reta é 1, a do plano vale 2 e a do espaço usual é 3,
coincidentes com a dimensão topológica. A figura 27 exibe
um fractal, chamado de esponja de Menger, que tem dimensão
fractal maior que 2
(dcap ≈ 2,727).
 |
| FIGURA
27 - Esponja de Menger |
Uma
característica estranha que surge logo à primeira vista, com
esses fractais, é a presença de dimensões que não são números
inteiros. Isso ocorre em aparente contradição com nossa 'intuição',
que espera que os objetos tenham dimensão inteira n = 1, 2,
3, etc.; a dimensão topológica, por sua definição exposta
acima, satisfaz essa propriedade 'intuitiva'. A dimensão (capacidade)
dos conjuntos fractais é maior ou igual à sua dimensão topológica.
Mas vamos procurar mostrar que a idéia de uma dimensão não-inteira
não é absurda, que ela pode ser expressa matematicamente de
forma coerente e que pode mesmo fornecer informações interessantes
sobre o grau de 'fractalidade' e de ocupação, pela estrutura
analisada, do espaço no qual está imersa. Note-se que poderão
existir fractais cuja dimensão é inteira; isso ocorre, por
exemplo, com a trajetória de uma partícula no movimento browniano,
cuja capacidade é 2.
Tomemos um exemplo concreto bem simples, e que já se tomou
clássico, para mostrar que a idéia de dimensão fracionária
não é tão absurda como parece: a medida do comprimento da
linha costeira de um país. Richardson chamou a atenção, em
1961, para o fato de que esse comprimento não é uma quantidade
bem definida como em geral se imagina: seu valor depende do
comprimento da 'régua' (unidade de medida) que é escolhida
para medi-la. Assim, se tomamos unidades de medida cada vez
menores (primeiro 10km, depois 1 km, em seguida 100m, e assim
sucessivamente), o comprimento da linha costeira, em função
de suas inúmeras reentrâncias, cresce proporcionalmente na
medida em que E (comprimento da 'régua' utilizada) decresce;
a relação, proveniente de (1), tem a forma: L(ε) ~ ε1-d,
onde d é a dimensão fractal. Esse tipo de dependência de uma
quantidade, no caso L, em relação a outra, ε neste caso,
é chamada de lei de potência.
Você poderá tomar um mapa, da Baía de Guanabara, por exemplo,
e verificar através da medida da periferia da baía, tomando
várias 'réguas' como sua unidade básica de medida, que a dimensão
fractal obtida, como ocorre com as linhas costeiras de outros
países analisadas por Richardson, fica em tomo de 1,25; trata-se
de um valor próximo da dimensão fractal da Curva de Koch,
embora esta seja um fractal exato e não estatístico.
Um
método de se medir a dimensão fractal de um conjunto: a contagem
por caixa
Nos
exemplos acima, como o processo de construção do conjunto
é bastante simples e sempre igual em cada escala, fica fácil
o cômputo da dimensão fractal. Para se medir a dimensão fractal
de estruturas naturais ou de fractais aproximados ou estatísticos,
devemos realizar uma análise mais cuidadosa. Notese que,
para objetos naturais, o processo de escalonamento tem limites
e só funciona dentro de uma certa faixa de escalas. Em geral,
se pode ir até uma certa escala inferior cujo valor é determinado
pelo tamanho dos constituintes elementares do objeto (ou pela
precisão das medidas), ou seja, chega-se a um ponto onde não
se pode mais ampliar as partes do objeto e ainda se obter
uma estrutura similar. O processo tem também um limite superior
dado pelo tamanho finito do objeto considerado. Existem vários
procedimentos de medição da dimensão fractal já propostos;
vamos discutir um deles e aplicá-lo a um conjunto importante,
no plano, que emana do estudo dos sistemas dinâmicos não-lineares.
O procedimento básico é o seguinte: divide-se a área (ou volume)
do conjunto analisado em um certo número de caixas (cubos
elementares) iguais. Conta-se o número de caixas em que existe
pelo menos um ponto do conjunto. Reduz-se sucessivamente o
tamanho das caixas e mede-se, a cada vez, o número de caixas
que possuem pelo menos um ponto do conjunto. Desenha-se o
gráfico do logaritmo de N (número de caixas ocupadas) em função
do logaritmo de (1/ε), onde ε é a dimensão linear
da caixa, em cada etapa. A dimensão fractal do conjunto é
dada pelo valor da inclinação do gráfico.
Consideremos o chamado Atrator de Hénon, uma figura
que surge quando aplicamos a seguinte transformação para obter
pontos sucessivos no plano (X,Y):
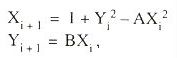 |
(2) |
com
A = 1,4 e B = 0,3. O atrator é obtido pela aplicação repetida
da regra acima: a partir do conhecimento do ponto inicial (X0,
Y0) a regra (2) permite que se determine o ponto
(Xl,Y1); a partir de (Xl,Y1)
a mesma regra leva ao ponto (X2,Y2), e
assim sucessivamente, num processo iterativo. A Figura 28 mostra
uma etapa do processo de determinação da dimensão fractal do
Atrator de Hénon. A inclinação do gráfico de log(N) versus
log(1/ε) nos dá a dimensão fractal aproximada desse
atrator; nesse caso, seu valor é d ≈ 1,2.
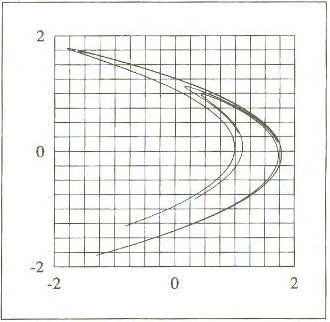 |
| FIGURA
28 - Atrator de Hénon e o cálculo de sua dimensão
fractal |
Esse
método de medida da dimensão fractal tem algumas limitações.
Ele não distingue caixas com números diferentes de pontos
e, portanto, não é muito adequado para descrever fractais
probabilísticos ou aqueles resultantes de um processo dinâmico
complicado, já que não permite determinar quais caixas são
visitadas com maior freqüência. Além disso, de um ponto de
vista operacional, o método converge lentamente e o número
de caixas necessário para se efetuar a medida cresce rapidamente,
tornando-se pouco prático para dimensões maiores que dois.
Existem outros métodos alternativos de medida da dimensão
fractal, mas não trataremos deles aqui. O leitor interessado
poderá consultar os livros citados nas referências, nos quais
alguns desses métodos são discutidos.
Outras
definições de dimensões fractais
Da
análise anterior, começa também a ficar claro que outras definições
de dimensão fractal são possíveis. De alguns anos para cá,
várias delas foram introduzidas, destacando aspectos variados
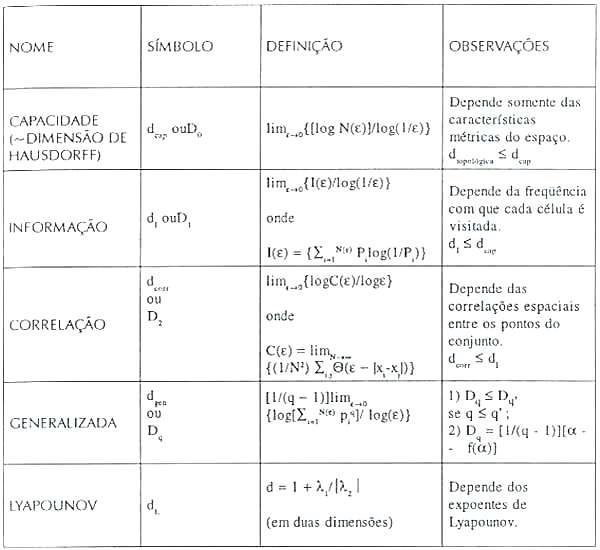
da 'fractalidade' de um conjunto. O Quadro 1 apresenta um
sumário das definições de dimensão mais utilizadas. Significativamente,
em 1983, foi definida uma noção de dimensão fractal generalizada
que incorpora muitas das definições anteriores em um esquema
único e progressivo.
Dimensão
de informação. É uma certa generalização da capacidade,
que leva em conta a probabilidade relativa de ocupação dos
cubos elementares usados para cobrir o conjunto. Fornece o
mesmo valor que a capacidade se as probabilidades de visita
a todos os cubos forem idênticas.
Dimensão
de correlação. Quantifica o número de pontos que estão
a uma distância menor que e de um dado ponto. A função
de correlação C (ε,r) mede o número de pontos situados
dentro de uma distância ε e a dimensão de correlação
é uma média disso, tomada sobre cada par de pontos. As três
definições anteriores de dimensão fractal podem ser vistas,
como se observa no Quadro 1, como casos particulares de uma
noção mais geral de dimensão fractal, denominada dimensão
generalizada, que caracteriza o conjunto através de todo
um espectro de dimensões. Com isso, estruturas fractais mais
complexas podem ser analisadas. Os conjuntos para os quais
as dimensões generalizadas Dq não fornecem resultados
idênticos são denominados de multifractais. Eles descrevem
situações em que diferentes regiões de um objeto têm diferentes
propriedades fractais.
Dimensão
de Lyapounov. Trata-se de uma noção de dimensão bem diversa
das anteriores. Está ligada ao comportamento temporal dos
sistemas dinâmicos. Parte-se, aqui, da idéia de que os expoentes
de Lyapounov (que medem a taxa exponencial média de esticamento
ou contração, em direções características, de trajetórias
que geram a figura de um atrator no espaço de fase) estão
relacionados à dimensão fractal do atrator. A definição dessa
dimensão, em duas dimensões, é: d = 1 + λ1/|λ2|,
onde os λi são os expoentes de Lyapounov.
Essa dimensão, que pode ser calculada computacionalmente,
é, em alguns casos, igual à dimensão fractal fornecida pelas
outras definições.
| Quadro
1 - Definições de dimensão fractal |
 |
---------------------------------------------------------------------------------------------------------------------------------
|