| Qual
a geometria da natureza? Essa pergunta não parece ter uma
resposta unívoca e precisa. Como Poincaré já chamava a atenção
no início deste século, ao discutir o uso da geometria euclidiana
ou de outras geometrias na descrição da estrutura do espaço-tempo,
a resposta a ela não é absoluta. Não existe uma geometria
intrínseca à natureza. Na tentativa de entender o seu entorno,
o homem constrói e utiliza conceitos geométricos, escolhendo
a geometria em função de sua comodidade e da maior adequação
à descrição dos fenômenos. A chamada geometria fractal,
da qual falaremos aqui e que trata dos conjuntos ou estruturas
fractais, embora esteja em uma fase ainda incipiente,
já ganhou, de alguns anos para cá, foros de um domínio científico
reconhecido. Ela tem se mostrado uma interessante fonte de
inspiração teórica e já encontrou aplicações variadas em muitas
áreas das ciências físicas e matemáticas.
Com
Galileu, no início do processo de matematização das 'leis
da natureza' , que veio a se transformar em uma das características
fundamentais da ciência moderna, vemos que são definidos,
de início, os entes matemáticos apropriados para essa descrição.
Para ele, embora a matemática seja "a língua na qual
a natureza está escrita", não se trata de utilizar qualquer
matemática, mas aquela que se expressa na linguagem das figuras
geométricas descritas por ou compostas de retas e curvas (suaves,
diríamos):
A
filosofia está escrita nesse enorme livro que temos aberto
diante dos olhos, o Universo. Mas não se pode entendê-lo antes
de se aprender a entender a língua, de se conhecer os caracteres
em que está escrito. Está escrito em língua matemática e seus
caracteres são triângulos, círculos e outras figuras geométricas,
sem as quais é impossível entender uma palavra sequer (...).
Esse trecho de Il saggiatore (O ensaiador), escrito
em 1623, é muito conhecido e citado. Abre, inclusive, o primeiro
capítulo de A geometria fractal da natureza (1975),
de Benoit Mandelbrot[1(a)],
considerado o livro que consolidou as bases da geometria fractal.
No entanto, uma outra passagem muito instrutiva de O ensaiador
é raramente mencionada. Nela, Galileu precisará ainda
mais o que entende pelos caracteres da língua necessária e
útil para descrever a natureza e eliminará claramente a possibilidade
de serem utilizadas 'linhas irregulares':
Chamamos
linhas regulares aquelas que (...) se podem definir e demonstrar
delas seus acidentes e propriedades. Assim, a espiral é regular
e se define dizendo que nasce de dois movimentos uniformes,
um reto e outro circular; assim, a elipse que nasce de secção
do cone e do cilindro. Porém, as linhas irregulares são aquelas
que, não tendo determinação alguma, são infinitas e (...)
indefiníveis. Não se pode demonstrar delas propriedade alguma,
nem definitivamente saber nada sobre elas. Dizer-se: "Tal
acidente ocorre graças a uma linha irregular", é o mesmo
que dizer: "Não sei por que ocorre". A introdução
de tal linha não é melhor que a introdução das simpatias,
antipatias, propriedades ocultas, influências e outros termos
usados por alguns filósofos como máscara da verdadeira resposta
que é "não sei".
Newton, no início do Prefácio à primeira edição de seus Princípios
matemáticos da filosofia natural (1686), uma das obras
mais importantes de toda a história da ciência, faz considerações
parecidas sobre as curvas nas quais a geometria se baseia:
(...)
a descrição de linhas retas e círculos, sobre as quais a geometria
se funda, pertence à mecânica. (...) é a glória da geometria
que de poucos princípios, tirados do nada, ela é capaz de
produzir tantas coisas.
Saltando mais de dois séculos, vamos reler trechos do grande
experimentador francês Jean Perrin, em seu livro Les atomes,
de 1913, no qual discute as evidências que levaram à comprovação
da existência dos átomos e moléculas. Perrin analisa, em particular,
seu trabalho experimental com o chamado movimento browniano,
sobre o qual realizou uma série de experiências minuciosas,
inspiradas em um trabalho teórico decisivo escrito por Einstein
em 1905.
Perrin estava estudando o movimento de uma partícula muito
pequena (um grão de pólen, por exemplo) dentro da água, quando
observado em um microscópio. A trajetória que a partícula
segue é extremamente irregular, no sentido de que muda de
rumo a cada instante; essa mudança é ocasionada pelos choques
com as moléculas do fluido que possuem um movimento de agitação
térmica (Figura 24).
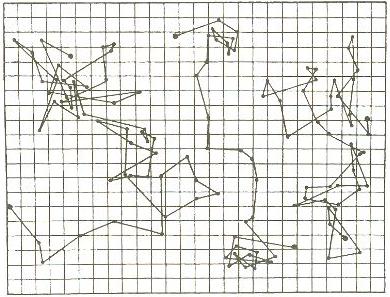 |
FIGURA 24 - Trajetória irregular do movimento browniano
de uma pequena partícula
mergulhada na água (desenhada por J. Perrin). |
Perrin
vai procurar convencer o leitor de que estas 'curvas irregulares'
- que não têm uma estrutura suave e para as quais não se pode
definir derivadas ao longo delas - podem ser utilizadas para
modelar várias situações que surgem na natureza e que, até
então, não tinham sido consideradas dignas de observação e
análise. Diz Perrin:
Aqueles
que ouvem falar de curvas [irregulares] sem tangentes, ou
de funções sem derivadas, pensam freqüentemente que a natureza
não apresenta tais complicações, e nem mesmo as sugere. O
contrário, contudo, é verdadeiro, e a lógica dos matemáticos
manteve-os mais próximos da realidade do que as representações
empregadas pelos físicos (...).
Quando Perrin fala dos matemáticos e de sua lógica, está se
referindo aos trabalhos de Riemann, Weierstrass, Cantor e
outros que, na segunda metade do século XIX, introduziram
e analisaram alguns monstros matemáticos, como funções
que não tinham derivada em nenhum ponto ou conjuntos particularmente
estranhos e complicados. Com certa perspectiva premonitória,
Perrin, depois de dar como exemplo de fenômeno natural irregular
o crescimento multiforme e dendrítico de um floco de neve,
acrescenta:
Poderíamos
encontrar situações nas quais o uso de uma função sem derivada
fosse mais simples do que o de uma função que pudesse ser
diferencíável. Quando isto ocorrer, o estudo matemático dos
contínuos irregulares provará seu valor prático... Contudo,
essa esperança é nada mais que um sonho, ainda.
Uma frase de Mandelbrot, escrita logo no primeiro parágrafo
do seu livro, ficou famosa por conter uma espécie de slogan
da nova geometria que se propunha: "Nuvens não são
esferas, montanhas não são cones, linhas costeiras não são
círculos, cascas de árvores não são suaves nem o raio se propaga
em linha reta". A contraposição proposital às colocações
de Galileu fica clara. Para se introduzir idéias científicas
novas e revolucionárias, o aspecto de convencimento dos leitores,
propagandístico diríamos, é também importante. Isso pode ser
visto, por exemplo, em várias afirmações de Galileu e nos
escritos de Mandelbrot. Nessas ocasiões são feitas afirmações
peremptórias, que posteriormente podem vir a ser consideradas
como exageradas, mas que fazem parte do jogo da ciência, uma
atividade humana e socialmente condicionada.
Nos modelos matemáticos construídos, ao longo dos últimos
séculos, para a descrição de fenômenos físicos e no uso tecnológico,
especialmente nas máquinas, predominaram sempre as formas
regulares: a reta, o círculo (roda), a esfera, o cilindro,
o triângulo, a elipse, a parábola e outras curvas similares.
As funções diferenciáveis (redutíveis à reta na vizinhança
do ponto) passaram a ser o ponto básico de partida para qualquer
modelo dinâmico na física e na matemática aplicadas. Sua utilidade
é inquestionável; mas seriam realmente as formas mais adequadas
para melhor descrever todas as inúmeras formas naturais,
inclusive as mais irregulares e multifacetadas? Com essa pergunta
e essa visão, externada por Perrin e Mandelbrot, entre outros
(ver o Apêndice para um sumário dos trabalhos pioneiros sobre
estruturas fractais), a idéia dos fractais começa a surgir...
Neste texto discutiremos, de forma introdutória e não isenta
de simplificações e omissões, os conceitos de fractal e de
dimensão fractal e mencionaremos algumas das aplicações que
essas idéias têm encontrado em diversos ramos do conhecimento.
O leitor interessado em se aprofundar no assunto poderá consultar
alguns dos livros listados nas referências (1 a 10)
.
--------------------------------------------------------------------------------------------------------------------------------- |
