Glossary of Terms
Aether/Ether (Luminiferous Ether) - The hypothetical medium that served as the carrier of light waves. In earlier centuries, the word ether was used to designate a ghostly substance that was believed to fill the upper regions of the universe beyond the orbit of the Moon. This word is sometimes spelled aether.
Calculus
of Variations
- A branch of matthematics that is a sort of
generalization of calculus. Calculus of variations seeks to find the path,
curve, surface, etc., for which a given function has a stationary value (which,
in physical problems, is usually a minimum or maximum).
Coordinate
System – A
coordinate system for a given space in Rn
is a rule that assigns an n-tuple of numbers (x1,
x2,
... , xn)
for each point in the space. The four most common coordinate systems are:
Cartesian, polar, cylindrical and spherical.
Ether/Aether (Luminiferous Ether) - The hypothetical medium that served as the carrier of light waves. In earlier centuries, the word ether was used to designate a ghostly substance that was believed to fill the upper regions of the universe beyond the orbit of the Moon. This word is sometimes spelled aether.
General 4-Tensor
- A General 4-tensor is a map from ttangent 4-vectors and generalized
1-forms to scalars.
Geodesic
– This term has
three equal definitions:
1) A geodesic is the straightest possible line in a curved space.
2) A geodesic is a path of extremal length.
3) A geodesic is a path in which there is zero acceleration in a Cartesian coordinate system as expressed in arbitrary coordinates.
For a mathematical
description of these definitions please see the link above.
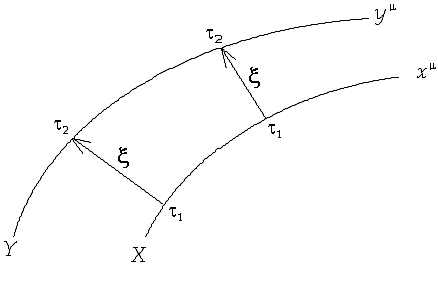
Geodesic
Deviation -
The relative separation of two test particles moving on closely spaced diverging
geodesics. Thus two particles in free-fall for which there are deviating
geodesics have a relative acceleration. See diagram below

[TBD]
Differential Manifold - Roughly speaking, a differential maniffold is an n-dimensional space Xn which can be covered by open neighborhoods on each of which coordinate systems may be defined in such a manner as to ensure that pairs of such systems are related to each other by differential coordinate transformations. A more exact definition is in the link.
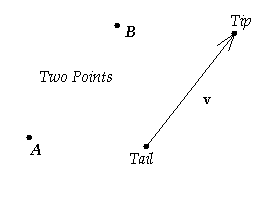
Displacement
Vector - A
vector is defined as a quantity that has a magnitude and a direction. Let there
be a directed line segment which has one end, designated as a tail, at
a point A and the other end, designated as the tip, located
at another distinct point B. See diagram below
Then one can imagine an
arrow with a tail and tip at points A and B
respectively as shown in the figure above. This arrow has both a magnitude and a
direction, which makes it a vector. It is a bilocal vector since there is
one point at which the vector is attached. This vector represents a displacement
from point A to point B.
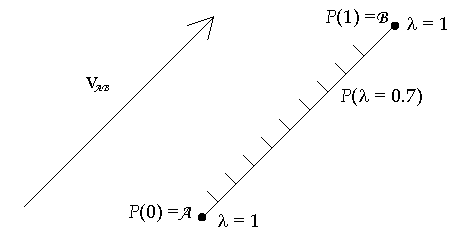
Tangent vector
- A tangent vector has a similar idea to thhat of a tangent to a line. Let the
tangent line be collinear with a vector and its direction determined by a
parameterization of the curve that the tangent line is tangent to at the point
on the line where the vectors tail is. See the diagram below
A vector, vAB defined
in this way is defined is the vector defined parametrically through vAB º
d/dl[A + l(B -
A)]
= B - A = P(1) - P(2) º
(tip)
- (tail
) º
(dP/dl)l
= 0. This type of
vector and can apply to only one point on a curved manifold. It is said to be a local
vector. While the bilocal vector has meaning only in flat space-time the local
vector always is always a well-defined quantity, i.e. in both flat and curved
spaces. For more on
vectors please see Tensors
– The Geometric View.
Inertial force – A force that must be added to Newton’s equations of motion when using a non-inertial frame of reference so that Newton’s laws will still be valid. See the link some comments and references on this subject.
Inertial
Mass – The
most common definition of inertial mass as used in relativity is known as Weyl’s
definition [1]. This definition starts with the following conservation law.
As applied to relativity Weyl’s definition of mass is as follows: In all
inertial frames of reference there are quantities, mk,
such that in a collision process, where there are n incoming particles
with velocities v1, v2,…,vn and p
outgoing particles with velocities v1+1,…,
v1+p
respectively, the equality
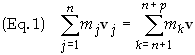
holds true [2]. Mass
defined in this way is sometimes referred to as relativistic mass. After m
is determined in this way the quantity p = mv becomes well
defined and is referred to as momentum. Thus once we known m we
can define momentum. So basically what Eq. (1) says is mass is defined such
that momentum is conserved. A derivation for the magnitude of m was
devised by Tolman and is very popular in relativity texts. For a derivation see Inertial
mass. This web page calculates the magnitude of a tardyon, i.e. a
particle for which v < c at all times. The magnitude thus found has the value
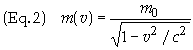
where m0
= m(0).
Invariance
- Certain quantities remain unchanged by a change in coordinates and thus in a
change in basis vectors as well. Let the old coordinates of the point P
be xb
and the new coordinates be
![]() where
where
![]()
Note: In this page the subscripts and superscripts will be Greek letters. These values will take on the same number of integers as the dimension of the manifold. In relativity the dimension of the manifold may be four. Consider the function F(xb). If, upon a change of coordinates,
![]()
and
the basis changes with the change in coordinates then F
is called a scalar, an invariant or a tensor of rank zero.
The change F Þ
F’ means only that
the function has a different functional form in the new coordinates. But the
mapping from point to real numbers remains unaltered.
Metric
Tensor - A
multilinear map from vectors to the set of real numbers that is used for
calculating the magnitude of a vector of the inner product of two vectors is
called the metric tensor and represented as g.
The metric tensor is defined such that it is symmetric.
Tensor - There are two commonly used definitions oof the term tensor (a) An tensor of rank (M, N) is a geometrical object whose components, which have M superscripts and N subscripts, transform from one set of generalized coordinates S to another set of generalized coordinates S ' by a particular rule. For a (2,0) tensor
![]()
A tensor of rank (M, N) tensor is a geometrical object defined on a manifold which is a multilinear map of M arbitrary tangent 1-forms and N arbitrary vectors into the set of real numbers, R. This may be expressed as
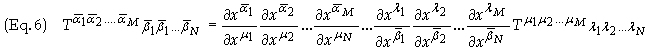
The definition of tensors as defined above is referred to as the analytic definition. For more information please see Tensors – The Analytic definition. Another definition is defined in terms of multilinear functions. For this definition please see Tensors – The Geometric View.
Lorentz Tensor - A Lorentz tensor is a map froom Lorentz 4-vectors and Lorentz 1-forms to scalars.
Orthogonal
transformation:
Any linear transformation
![]() that has the property
that has the property
![]() is
called an orthogonal transformation and
is
called an orthogonal transformation and
![]() is known as the orthogonality
condition.
is known as the orthogonality
condition.
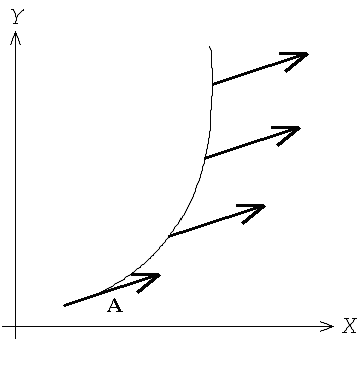
Parallel
Transport - To parallel transport a vector means to move the vector
along a curve while keeping the vector, defined on each point on the curve,
pointing in the same direction. See diagram below
Spacetime
– The manifold
of all possible events where an event consists of a point in space at a
momentum of time and represented by a 4-tuple. In Lorentz coordinates the 4-tuple
is expressed as (ct, x, y, z).
Total
Derivative – The
total derivative of a vector P is defined as
![]()
References:
[1] Philosophy
of Mathematics and Natural Science,
Herman Weyl, Princeton University Press, (1949), page 139.
[2] The
Classical and Relativistic Concepts of Mass, Erik Eriksen and Kjell Voyenli, Foundations
of Physics, Vol. 6, No. 1, (1976).