Introduction to Manifolds
Back
to Physics World
Back to GR Math
Definition of Manifold:
Let Rn,
represent the set of all n-tupules of real numbers (x1,
x2,
x3
, … , xn).
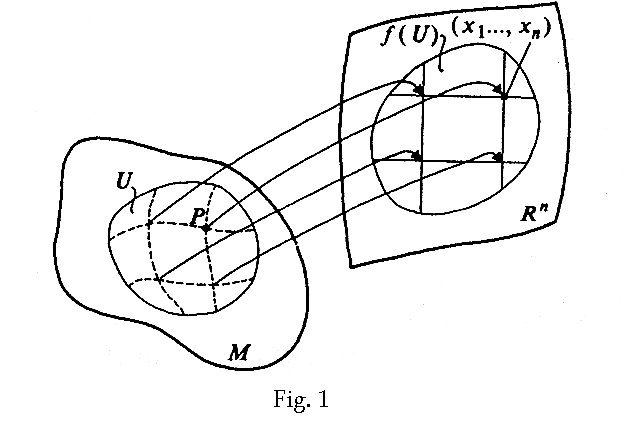
A manifold is a set of ‘points’ M for which each point of M
has an open neighborhood that has a continuous 1-to-1 map onto an open set
of Rn
for some n. This simply means that M is locally ‘like’ Rn,.
The dimension of the manifold is, obviously, n. It is important that the
definition involves only open sets and not the whole of M and Rn,
because we do not want to restrict the global topology of M. The map is
only required to be 1-to-1 and not to preserve lengths or angles. Length is not
defined at this level of geometry. In some physical applications the notion of
the distance between two points is not required.
By definition, a map
associates a point P of M an n-tuple (x1(P),
x2(P),
x3(P),
… , xn(P)).
The numbers x1(P),
x2(P),
x3(P),
… , xn(P)
are called the coordinates of P under this map as illustrated in
Fig. 1. below

The
superscripts do not indicate powers of x(P), they indicate
an index to refer to a particular variable.
One way of thinking about a manifold is that it is simply any set of
points which can be given n independent coordinates in some neighborhood
of any point, since these coordinates actually define the required map to
Rn.
At this point the reader
should have a general idea of what a manifold is.
To understand more we must understand the nature of these coordinate
maps. Let f be a 1-to-1 map
from a neighborhood U of a point P of M onto an open set f
(U)
of Rn as illustrated in Fig 1. The neighborhood need not contain all of M so
there will be neighborhoods with there own maps and each point of M must
lie in at least one such neighborhood. The pair consisting of a neighborhood U
and its map f is called a chart and denoted (U, f).
It is easy to see that these open neighborhoods must have overlaps if all points
of M are to be included in at least one, and it is therefore overlaps
which enable us to give further characterization of the manifold. See Fig. 2
below
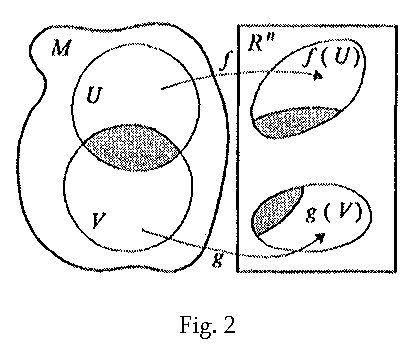
As
shown in the diagram we have chosen two overlapping neighborhoods, U and V.
As shown in Fig. 2 the neighborhood U is mapped into Rn
by f while V is mapped into Rn
by g. U Ç
V is open and is
given two different coordinate systems by the two different maps. There is
therefore an equation relating the two coordinate systems. To find it, pick a
point in the image of U Ç V
under f (i.e. a point in Rn).
Refer to this point as (x1,
x2,
x3,
… , xn).
As shown in Fig. 3 below
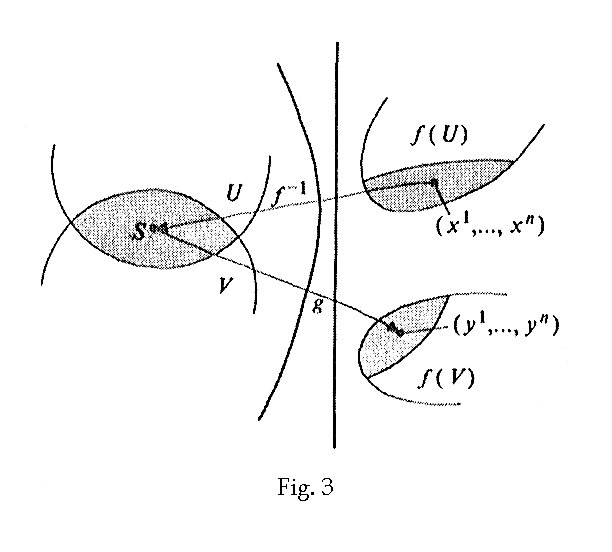
Since f is 1-to-1
then it has an inverse map f
-1,
so there is a unique point in U Ç
V which
has these coordinates under f. Now
let g take us from S to another point in Rn,
say (y1,
y2,
y3,
… , yn).
We have thus constructed the function g(f
-1)
which is expressed as
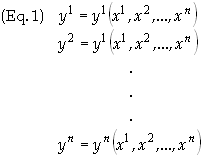
which is called a coordinate transformation. If the partial derivatives of order k or less of all these functions {yi} with respect to the {xi} exist and are continuous, then the maps f and g are said to be Ck related. It is possible to construct a whole system of charts, called an atlas, in such a way that every point in M is in at least one neighborhood and every chart is Ck related to every other one it over laps with, then the manifold is said to be a Ck manifold. A manifold of class C1 is said to be a differential manifold.
References
[1] Geometrical methods of mathematical physics, by Bernard F. Schutz, Cambridge University Press, page 23.