Tensors – The
Geometric View
Back to Physics World
Back
to Geometrical Math for GR
Vectors
In order to define tensors, we must first define vectors and 1-forms. There are several ways to define the term vector. Misner, Thorne and Wheeler (MTW) [1] present the first three definitions given below while Schutz gives the fourth and fifth. [2][3]
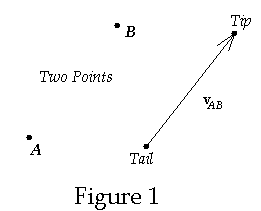
Definition (1) of vector: As an arrow. This is illustrated in the right hand side of the diagram below. In many cases a vector will be defined with respect to two points on a manifold, the vector being an arrow with its “tail” at one point and its “tip” at the other point. Such a vector is known as a bilocal vector. A vector defined by two such events is shown in the diagram below
An example of such a vector on a flat manifold is the displacement vector, DX. The dimension of this manifold is three. If it is agreed among readers that the tail is to be designated as the ‘origin’ of coordinates then the spacetime displacement forms a 1-to-1 correspondence with the event such as X, which is then referred to as the position vector and labeled R = (ct, x, y, z) which lies within the manifold itself. Such a geometrical object is referred to as a bilocal object. The position vector is an example of what is known as a position vector. Position vectors exist only on flat manifolds. The vector VAB is defined as the directed line segment, i.e.
Definition (2) of a vector: As a parameterized line. See figure below
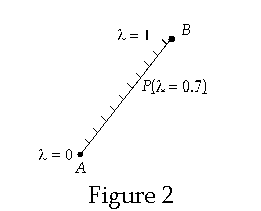
The vector VAB is defined in this case as
Such a vector is located
at the point A on the manifold and in this case is not a bilocal vector.
Definition (3) of a vector: As derivative of a point along a curve – See figure below
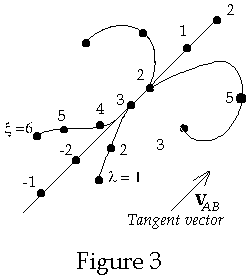
The
vector VAB
is defined in this case as
There
is another definition of vector that finds wide use in differential geometry.
For example; the following definition of vector is found in Schutz [2].
It is defined as follows:
Definition (4) of a vector: A general vector is defined as a collection of numbers (its components in some coordinate system, say O)
and by the rule that its components in a coordinate system O transform to another coordinate system O’ as
The
over bars on the indices represent the components of the vector A in the
new coordinate system.
Definition
(5) of a vector: A
vector is a map from 1-forms into real numbers.
Definitions (3), (4) and (5) are the only definitions that applies to both flat and curved spaces. In such cases the vector is localized to a point on the manifold and cannot be moved around without discrimination. Vectors can be added by adding their components, i.e.
Bold
face letters normally represents vectors. The last definition of a vector is
given in terms of differential operators as can be found in Schutz [2]. Thus
Definition (5) of a vector: A general vector is defined as a differential operator
Basis
Vectors
A
basis is a linearly independent spanning set for a vector space. The
elements of a basis are called basis vectors. By definition any vector at
a any point P. on the manifold can be expressed as a linear combination
of basis vectors
where
Einstein’s
summation convention, which was used in Eq. (8), states that if a twice repeated
index appears in an expression, once as a superscript and once as a subscript
then summation is implied over the range of values the index may take on. If the
indices are Latin then they take on the numbers 1, 2, 3 and if they are Greek
they take on the numbers 0, 1, 2, 3 (other authors prefer to use the numbers 1,
2, 3, 4 instead). For example: The vector p can be expressed in terms of
a basis vectors as p = paea.
In any frame O there are four special vectors, defined by giving their components:
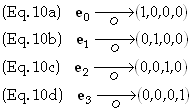
Any
vector can be expressed as a linear sum of such vectors. These definitions
define the basis vectors of the coordinate system O. Similarly in another
coordinate system O’ the basis vectors become
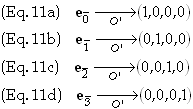
Any vector can be represented in terms of either basis, i.e.
The numbers Aa are called the components of the vector A in the coordinate system in which the basis vectors are ea.
Transformation
of Basis Vectors
A
vector does not rely on a particular coordinate system for its definition.
Unlike a typical vector the basis vectors change when the coordinate system
changes since basis vectors are defined in terms of the coordinate system. That
any vector can be expressed in terms of different coordinate systems is
expressed in Eq. (12) above. From that expression we can deduce the basis vector
transformation law. Substituting Eq. (5) into Eq. (12) results in
Since these are just numbers they can be rearranged as
Now
we use the fact that b
and
are dummy indices: we change b to a
and
to
,
Writing Eq. (15) as
Since Eq. (16) must be true for all vectors A it follows that
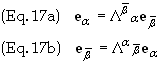
Eq. (17a) holds for all
basis vector transformations and thus gives the transformation rule for changing
basis vectors. Eq. (17b) is the transformation from the old system to the new
system and readily follows from Eq. (17a) by a mere change of variables. Eq.
(17) is not a component transformation: it is a basis {ea}
transformation between O and O’ as a linear sums over the basis
vectors.
1-forms
A 1-form is a linear map from vectors in Rn into the set of real numbers R. The set of 1-forms is a vector space that is dual to the space of vectors as will be explained below. 1-forms are vectors in this sense but are referred to as the vectors dual to the set of vectors in Rn. For this reason the space dual to Rn is labeled *Rn. A smaller case bold letter often represents a 1-form with a tilde over it as thus
Linearity implies that
A basis for the space duel
to the vector space is a quite similar to that of the original vector space. The
dual vector space *Rn
has n linearly independent 1-forms for which an arbitrary 1-form in the space
can be represented as a linear sum of these basis 1-forms. Thus a 1-form
could be represented in terms of a
set of 1-form bases 1-forms
as follows
Once again we have employed Einstein’s summation convention in Eq. (20). This is possible due to our placement of the superscript and the subscript on components and basis 1-forms. Since the bases 1-forms are linearly independent we find that
The components of a 1-form on a basis vector are defined as
Eq. (23) can then be expressed as
Eq. (23) is referred to as
the contraction of
with A. We have one last deduction to make. We know that a 1-form maps a
vector into a real number. This real number is basis independent and is thus
referred to a tensor of rank one or a scalar. Mapping the vector A
by the 1-form
gives the scalar
This can only be an equality if
Basis
1-forms
By
definition a basis 1-form is one of a set of 1-forms, the
collection of which is called a dual basis. A dual basis can be
used to express any 1-form in the dual space by the 1-form as a linear
combination of the basis 1-forms. For example: The 1-form
can be expressed in terms of a
basis 1-forms as
. Comparing with Eq. (10), we see that Eq. (25) gives the bth
component of the ath
basis 1-form. We can write this out as
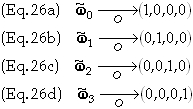
Any 1-form can be expressed as a linear sum of basis 1-forms. These definitions define the basis 1-forms of the coordinate system O. Similarly in another coordinate system O’ the basis 1-forms become
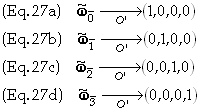
Transformation
of Basis 1-Forms
We are now in position to determine how the basis 1-forms transform. Start with the scalar product of a vector and a 1-form to obtain
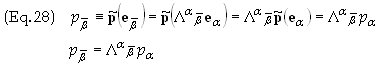
In Eq. (28) we have first
placed in the transformation equation of the basis vectors, i.e. Eq. (17).
Transforming from the old basis to the new one is readily seen to be
The definition of a 1-form does not rely on what coordinate system and basis the 1-form is expressed in. For this reason, analogous to Eq. (12) we can express any one form in either basis, i.e.
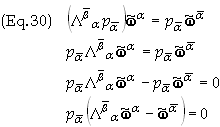
Since
this equation must be true for all 1-forms and since
is
an arbitrary 1-form we deduce that
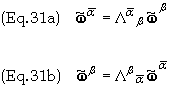
Eq. (31b) follows from Eq.
(31a) by a mere change in indices. Eq. (31) gives the transformation rule for
changing basis 1-forms from one coordinate system to another.
Tensors
A
tensor of type (aka valence) (n, m) is a
multi-linear map that maps n 4-vectors in Rn
and m 1-forms in *Rn
into the set of
real numbers. The rank of a tensor is defined as n +m. This is
expressed as
A tensor T of type 2x2 is of the form
Multi-linearity means that
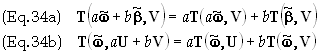
Types of Tensors
A
function, such as a tensor, depends not only on the functions output given its
input but it also depends on the domain of the input. Those tensors for which
the domain is restricted to affine vectors and affine 1-forms are referred to as
affine tensors. In spacetime physics the term Lorentz tensor
refers to those tensors for which the input are all either Lorentz vectors or
Lorentz 1-forms. The prototype for a Lorentz vector is any 4-vector which
transforms the position 4-vector X = (ct, x, y, z)
from one Lorentz coordinate system to another. A tensor which maps generalized
4-vectors and their associated 1-forms is referred to as a generalized
4-vector.
Tensor Components
The components of tensors are defined as through the action of basis vectors and basis 1-forms, i.e. consider a tensor of type (1, 3) and substitute in a basis 1-form and three basis vectors to obtain
The
components are covariant quantities, not invariant quantities, because they will
change upon a new choice of coordinate systems.
We
start with Eq. (35) expressed in terms of the new coordinates, i.e.
The transformation from
one basis to another is obtained by substituting the transformation for 1-forms
from Eq. (31) and the transformation for basis vectors from Eq. (17) to get
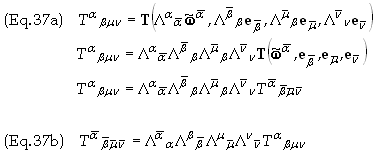
Eq. (37b) is obtained from Eq. (37a) by a change in variables using Eq. (37a) as a template.
The Metric Tensor
The scalar product of two vectors A and B is defined, in Lorentz coordinates = (ct, x, y, z) where the frame is inertial, as defined as
We take g(_ ,_ ) as a function of two arguments, i.e. vectors, and is linear on each argument. Then as in the above case
where
gab
are the components of the metric tensor. In Lorentz coordinates the scalar
product of two 4-vectors
The most common use for the metric tensor is to define intervals (not lengths) on a manifold. I.e.
References:
[1] Gravitation,
Misner, Thorne and Wheeler, W.H. Freedman & Co., (1971). Page 49 to
50.
[2] A first course in general relativity, by Bernard F. Schutz, Cambridge
University Press, (1990). See page 39.
[3] Ref. 2, page 128.