Inertial Mass

Back to Physics World
Back to Special Relativity

The concept of inertial mass is physics has been described in various ways. In classical Newtonian mechanics Mach’s definition is often used. From herein if the term mass is used unqualified then it referrers to the inertial mass of the object.  This definition assumes Newton’s third law to  

Newton’s Third Law: For every action there is an equal and opposite reaction.

For example: If body 1 exerts a force of F₂₁  on body 2 and body 2 exerts a force F₁₂ on body 1 then 

Force is defined as the time rate of momentum, p, where p is defined as the product of mass m and velocity v. That is

The mass of any body is always taken as a positive quantity. This is contrary to the popular belief that force is defined as

However if the mass is constant then m can be taken outside the derivative and there yields the equality f = ma. If m₁ is the mass of body 1 that has an acceleration of a₁ and m₂ is the mass of body 1 that has an acceleration of a₂, each body having a constant mass, then

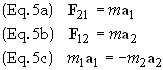
Eq. (5c) can be written in terms of the magnitudes of acceleration as

Eq. (6) embodies what is known as Mach’s definition of mass. Thus, in Newtonian mechanics, if two bodies are allowed to exert equal and opposite forces on each other then the mass of any body can be given once a standard body is defined. I.e. if we let m₁ be the mass standard then m₂ is determined. Another definition, one that is valid in both Newtonian and special relativity, is based on The Principle of Conservation of Momentum. In regards to this situation Herman Weyl wrote [1]

According to Galileo the same inert mass is attributed to two bodies if neither overruns the other when driven with equal velocities (they may be imagined to stick together upon collision).

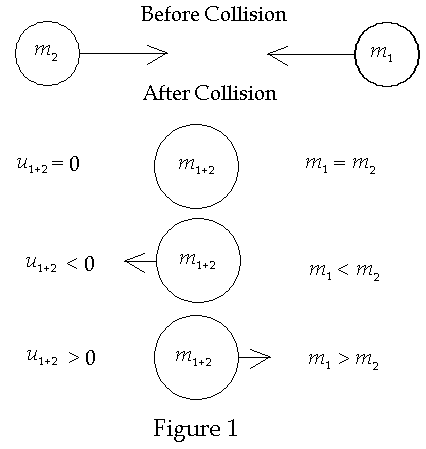
This is known as Weyl’s definition of mass [2]. This is illustrated in Figure 1 below. It follows that if u₁₊₂ = 0 then m₁ = m₂, if v₁₊₂ < 0 then m₁ < m₂ and if v₁₊₂ > 0 then m₁ > m₂.  See Figure 1

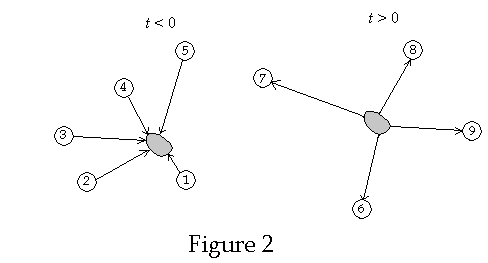
Consider a system of particles that collide at the same event where n particles go into the collision and p particles come out of the collision. I.e. particles 1 to n are the n particles that go into the collision. Particles n +1 to n + p are the p particles that come out of the collision.  This is illustrated in Figure 2 below where as an example we have set n = 5 and p = 4.

We will use this diagram and examine in detail the principle of conservation of momentum which states that there are quantities mk, called the inertial mass of the kth particle, such that that in any collision process, where there are n incoming particles with velocities v₁,…, v_n and p outgoing particles with velocities v₁₊₁,…, v_n+p respectively, the equality

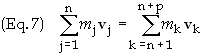
holds in all inertial frames of reference. The quantity p = m_kv_k is defined as the linear 3-momentum of the kth particle. Note: Mass defined in this way is sometimes referred to as relativistic mass. After m is determined in this way the quantity p = mv is well defined. Thus once we known m we can define momentum. So basically what Eq. (1) says is mass is defined such that momentum is conserved. A derivation for the magnitude of m was devised by Tolman and is very popular in relativity texts.
    One of the earliest concepts of a mass in relativity was written up in Einstein’s famous 1905 paper On the Electrodynamics of Moving Bodies” where he spoke of longitudinal and transverse mass [4]. These were defined as the coefficient of proportionality between the force as measured in the rest frame to acceleration in the moving frame. This definition never caught on since now physicists only write equations such that all quantities are expressed in the same frame. This led to a different value for transverse mass than Einstein used. Einstein used the electric force, i.e. the force on a charged particle, as an example. In the year that followed Max Planck showed that Einstein’s relation could be written in the form [5] 

where

where m₀  = m(0) is the proper mass or rest mass of the particle. Taking relativity on a new course, Richard C. Tolman and Gilbert N. Lewis objected to the fact that relativistic mechanics was so far based on electrodynamics in that the expression for the velocity dependence on mass had been derived from electrodynamics.  Tolman and Lewis were convinced that mass should [6]

… be obtained merely from the conservation laws and the principle of relativity, without any reference to electromagnetics

Mass of a Tardyon 

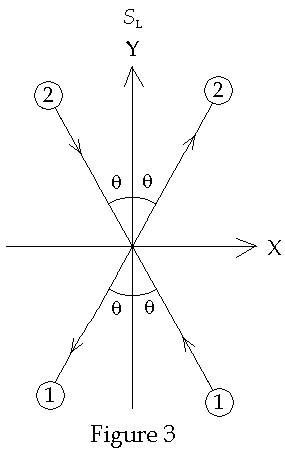
Now consider the same collision from an inertial frame it S’ that has the same x-component of velocity as particle 1.  The velocity of particle 1 will have no component in the y-direction but will initially have a speed in the +y’-direction of v₀. After the collision particle 1 will move in the –y’-direction with speed of magnitude u₀. See Fig. 3 below

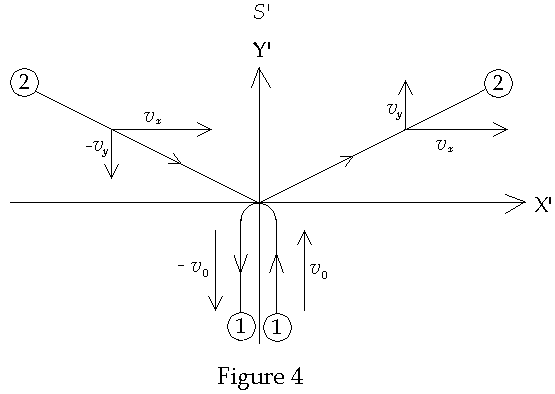
Prior to the collision particle 2 will move in the –x’-direction with speed of magnitude v_x and in the –y’-direction with speed of magnitude v_y. If we observe this same collision in the frame in which particle 2 has no x-component of velocity then we have the situation described in Fig. 4 below.

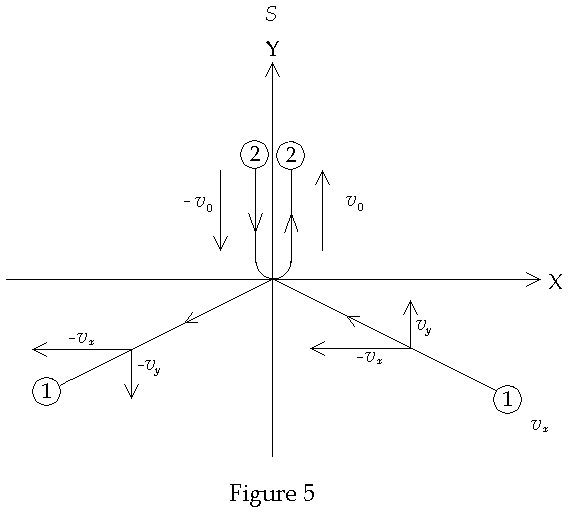
S’ moves relative to S in the +x-direction with speed v_x.  It can be shown that the relationship between the y and y’ components of velocity of the particles is given by

Thus since u_x = 0, v_y = v₀ and u_y = v_y we have  

In S’ particle 1 moves with a speed V given by  

It will be assumed that the mass of a particle is at most a function of the particles speed. As observed from S, conservation of the y-component of momentum demands, upon applying Eq. (11), gives

Solving for m(v) gives

Substituting Eq. (15) into Eq. (18) gives

Define the proper mass m₀ of the particle as

Since this relation must hold under all conditions it must also hold for small values of v₀. Therefore

Mass of a Luxon 

The procedure above assumes that v < c. We now ask - What is the mass of a particle which travels at the speed of light? Such particles are known as luxons. A photon is the most well known example of a luxon. To find the mass of a luxon we first express Eq. (17) as

where E = gmc² is the total inertial energy (kinetic energy + rest energy) of the particle. For luxons E = pc and therefore m₀ = 0. Therefore we have the important result - The proper mass of a photon is zero! This also means that the proper mass of any luxon is zero. However the (inertial/relativistic) mass of photons/luxons is still l related to its momentum by m = p/v. Since v = c and  m = pc then 

which is to be expected from E = mc² . Notice that this relation does not define mass. It is a relationship between the particles mass and its energy. In that sense the relation is a consequence of the definition m = p/v and the energy-momentum relation E = pc. Since the energy of a photon is related to the photon’s frequency by E = hf then Eq. (2) can be expressed as 

References:

[1] Philosophy of Mathematics and Natural Science, Herman Weyl, Princeton University Press, (1949), page 139.  
[2] Concepts of Mass in Contemporary Physics and Philosophy, Mass Jammer, Princeton University Press, (2000), page 9.
[3] The Classical and Relativistic Concepts of Mass, Erik Eriksen and Kjell Voyenli, Foundations of Physics, Vol. 6, No. 1,  (1976).  
[4] On the Electrodynamics of Moving Bodies, Albert Einstein, Annalen der Physik , 17, (1905).  
[5] Das Prinzip der Relativitat und die Grundgleichungen der Mechanik, Max Planck, Verhandlungen der Deutschen Physikalischen Gesellschaft, 4 131, 136-141 (1906).  
[6] The Principle of Relativity and Non-Newtonian Mechanics, R.C. Tolman and G.N. Lewis, Philosophical Magazine, 18, (1909), pg. 510-523.  
[7] Non-Newtonian Mechanics: The mass of a moving body, R.C. Tolman, Philosophical Magazine, 23, (1912), pg. 375-380.

Back to Special Relativity
Back to Physics World