Invariance

Back to Physics World
Back to Geometrical Math for GR

Certain quantities remain unchanged by a change in coordinates and thus in a change in basis vectors as well. Let the old coordinates of the point P be x^b and the new coordinates be where

Note: In this page the subscripts and superscripts will be Greek letters. These values will take on the same number of integers as the dimension of the manifold. In relativity the dimension of the manifold may be four. Consider the function F(x^b). If, upon a change of coordinates,

and the basis changes with the change in coordinates then F is called a scalar, an invariant or a tensor of rank zero. The change F Þ F’ means only that the function has a different functional form in the new coordinates. But the mapping from point to real numbers remains unaltered. An example of a scalar is the scalar product of two vectors. Let A and B be two vectors. Then the scalar product is represented as

where g_ab are the components of the metric tensor. Summation is implied over the valid range of the subscripts and superscripts. Am are the contravariant components of A and B_m are the covariant components of B.  It A and B are general vectors then, by definition 

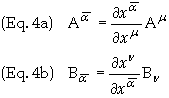
where, for an allowable coordinate transformation

 where  is called the Kronecker delta and has the value of 1 when the arguments (i.e. the superscript/subscript) and zero otherwise. Substitution of these values into Eq. (3) gives 

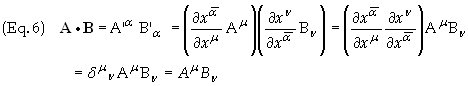
 It should be noted that the components of a vector are not scalars. However there is a caveat to this that should be explored. Consider vectors in Euclidean geometry. For simplicity we restrict our attention to examples where all the vectors are in a plane. In Cartesian coordinates the metric tensor is the Kronecker delta and the covariant components equal the contravariant components. Any vector can be expressed in terms of a set of basis vectors. The unit vectors i and j take on their usual meaning, i.e. they are vectors of unit length pointing in the positive direction of the x-axis and y-axis respectively. We will consider vectors in two coordinate systems, one that is rotated relative to the first where the unit vectors in the rotated system point along the x’-axis and the y’–axis and are labeled i’ and j’ respectively. Any vector R can be expressed in either coordinate system. For example: R can be written as

See Fig. 1 below

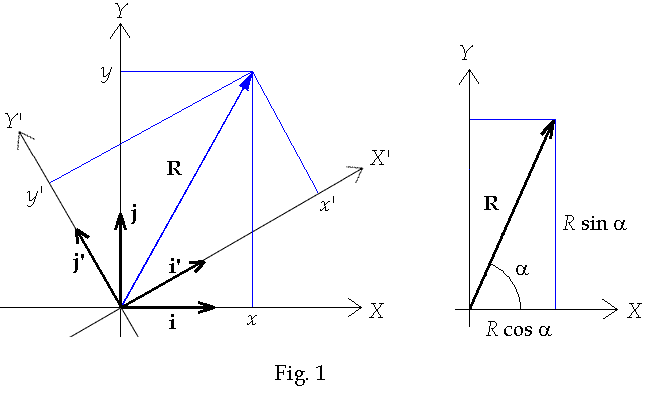
or as

Given any two Euclidean vectors A and B it can be shown that

In Eq. (9) A and B are the magnitudes of the vectors A and B respectively and f is the angle between the two vectors. It follows that

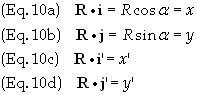
Here is the caveat mentioned above. While x and y are the components of the vector R and the components of a vector change upon change in the coordinate system it also follows that x and y are the values of two scalar products and are therefore invariant with respect to a coordinate transformation. To be precise, x will not change with a change of coordinates since x is the projection of R in the direction of i and this has an invariant meaning.  The vector i does not change upon a change of coordinates. The reason is as follows: Both R and i are vectors and as such the scalar product of these two vectors is an invariant, in this case the invariant is the value x. This means that if both R and i are expressed in terms of components of another coordinate system then the dot product will remain unaffected. Graphically this means that the dot product of R and i has the value of the component in the direction of i that is therefore a quantity which is coordinate independent. As can be seen from Fig. 2

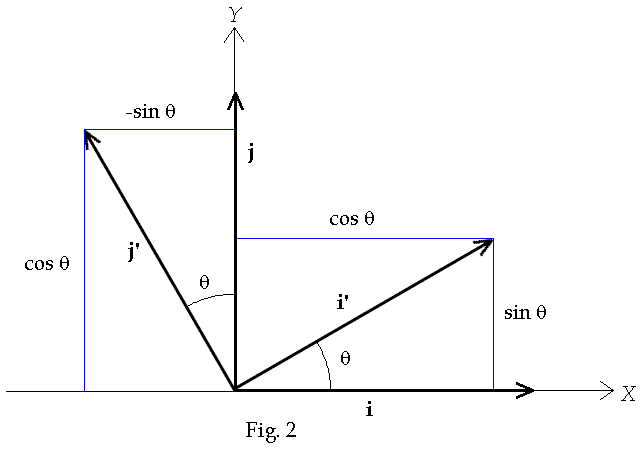
i’ and j’ can be expressed in terms of i and j basis vectors as

 Solving Eq. (11) for i and j in terms of i’ and j’ gives

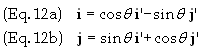
R can be expressed in terms of the new coordinate system as shown in Fig. 3 below (The unit vectors are not drawn to keep the diagram from being too cluttered).

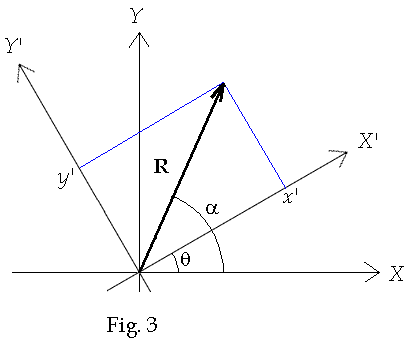
 In the new coordinates the R is written as

 Therefore

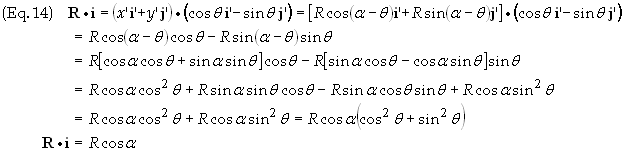
In special relativity there is a similar situation. Let the 4-momentum of a particle be 

where m is the mass of the particle and E = mc² is the free-particle energy. Let the 4-velocity of a particular observer be

where v_obs is the 3-velocity of the observer and  

Consider the quantity  

If we choose to evaluate these quantities in the rest frame of the observer then 

where e0 is a 4-vector pointing in the direction of increasing time as measured in the rest frame of the observer. Using Minkowski coordinates (t, x, y, z) the metric tensor becomes h_mn = diag(1, -1, -1, -1). Using these the scalar productt in Eq. (17) becomes 

Thus in this context m is an invariant. It’s referred to as the “mass measured by observer” and as such there is no ambiguity to the value of mobs since all agree on what observer measures. The time component of the 4-momentum of a particle is the mass as measured by the observer of the current frame. That too is unique if we keep in mind that the frame itself has an identity all its own. Without the subscript m refers to the current frame observer.  

Back to Geometrical Math for GR
Back to Physics World