Geodesics

Back to Physics World
Back to Geometrical Math for GR

Straightest Possible Line in a Curved Space

The first definition states that a geodesic is the straightest possible line in a curved space. Here we use affine geometry in which the space is explored by parallel transport. The term affine means connected and refers to how parallel lines are connected.
     Let l be an affine parameter which parameterizes the curve which is to be expressed in generalized coordinates q. Then the geodesic can be defined by demanding parallel transport of the tangent vector along the curve. I.e.

where

is the covariant derivative of U^m. Note that according to the chain rule

Eq. (2) can now be expressed as

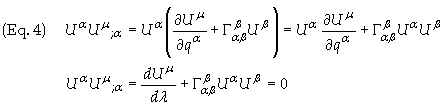
Substituting

into Eq. (3) gives the final result, i.e. the Geodesic Equation

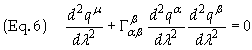
Path of Extremal Length

The second definition states that a geodesic is a path of extremal length. Here we use metric geometry in which the space is explored by measuring distances. The term metric means 'to measure' and we use it to measure the path which has an extreme length.
     Let l be an affine parameter, which parameterizes the curve that is to be expressed in generalized coordinates q^a. Consider the length of a curve as defined as the integral of ds, where where ds² = g_abdq^adq^b and  

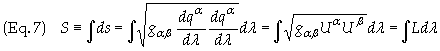
where L is defined as

An integral is said to be extremal when its first variation vanishes, i.e. dS = 0. As such L satisfies the Euler-Lagrange Equations

Carrying out the differentiation (note that g_ab is not a function of U^m) is a bit complicated but can be made simple by starting with L² to obtain

We can now utilize Eq. (10) to make things easy in the calculations to come.

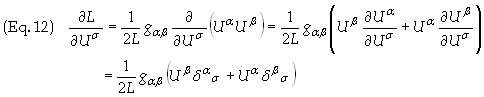
where . d^a_b is the Kronecker delta. Therefore

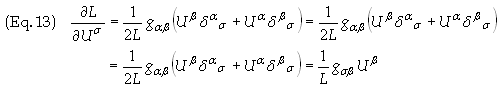
If l is chosen to be arc length then ds = dl from which it  follows that and therefore L = 1. Taking the derivative of the first term in Eq. (11) with respect to l gives

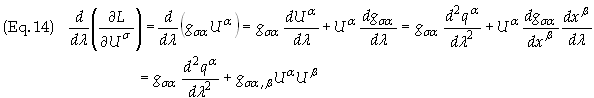
Taking the derivative of the first term in Eq. (11) with respect to q^s gives

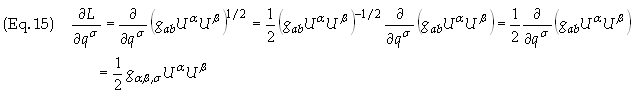
In Eq. (13) we have used the relation  obtained above to simplify Eq. (13). Substituting Eq. (12) and (13) into Eq. (7) gives

To put this in a more familiar and compact form rewrite Eq. (14) as

Multiplying Eq. (11) through by g^sn gives (note:  g^sng_sm = dⁿ_m )

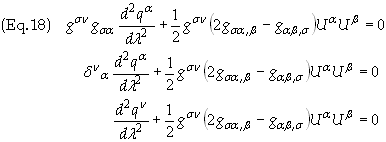
Since  Eq. (11) can rewritten as

Relabel once more with n = m.  Substitute the Christoffel symbols of the second kind, i.e.

Which, again, is the geodesic equation as derived at the top but now with a different, equivalent, definition.

Change Coordinates from Locally Flat Coordinates

The third definition is similar to the first in that we define a geodesic, as the path, which is identical to zero acceleration of a point, as expressed in Cartesian coordinates equals zero. I.e. a straight line whose equation is given by

We now take that equation and express it in generalized coordinates. The Cartesian coordinates xa can be expressed in generalized coordinates x^a = x^a (q^a). Substituting into Eq. (16) and applying the chain rule we get

Taking the second derivative gives

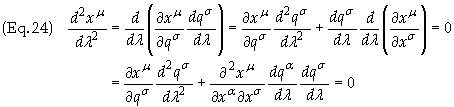
Multiply through by ¶qⁿ /¶x^m  

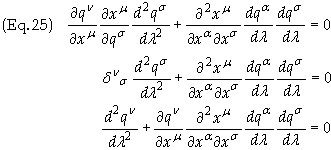
where the relation

was employed to simplify Eq (25). It can be shown that

Substituting this expression into Eq. (16), and relabeling indices, once again yields

Back to Geometrical Math for GR
Back to Physics World