Coordinate Systems
Back
to Physics World
Back
to GR Math
This section is a brief, but general, review of coordinate system using, as examples, the four most common coordinate systems: Cartesian, polar, cylindrical and spherical. As with any branch of mathematics and physics there are terms which remain undefined, the meaning of which is assumed. In geometry the most basic geometry object, and thus the term which remains undefined, is point. A point can be thought of, intuitively, as an infinitely small physical object with no structure. A point may represent any number of things such as the position of an object, the electric field near a charged particle, the temperature at a given place of a piece of metal etc. The collection to which a point belongs is called a space. Most, but not all, geometrical objects are defined in terms of points. For example; the definition of line segment is the collection of all points that are in-between two given points where in-between is yet another undefined term. To describe geometrical objects analytically requires the use of numbers. If a point can be uniquely specified in the space with a minimum of n numbers, each of which is called a coordinate, then the space is said to be n-dimensional. The world in which we live is three-dimensional since we can locate any point (i.e. any location) with a minimum of three and numbers once a reference system is defined. For example, if one is in a rectangular room then one can uniquely locate any point in the room with three and only three numbers each of which represents the distance the point is from each wall. Three-dimensional space will be referred to hereafter as 3-space and denoted R3. However it should be kept in mind that the given "space" may not refer to the physical three-dimensional world in which we live.
As noted above the position of a point in Rn can be represented using exactly n numbers. Each coordinate is assigned a real number thus giving a set of n real numbers (x1, x2, ... , xn ) the superscripts are not to be interpreted as a power but rather as a label), which then uniquely defines the point in Rn.
Sometimes a label will appear as a superscript or as a subscript. Such a label is referred to as an index. Such a point may be given a label, such as P or Q, and the coordinates will at times be given next to the label such as P(x1, x2, ... , xn). However it is the point P itself that has a geometrical meaning whereas the coordinates themselves do not. This follows from the fact that there is no unique way to assign coordinates to a point. For example the point P(x, y, z) in R3 is thus referred to as the point P whose coordinates are x, y, and z. The coordinates may be chosen in a multitude of ways. The system used to identify the numbers with the point is called a coordinate system. The coordinate system one chooses is usually based on the symmetry of the problem being considered or by various restrictions imposed on the problem such as motion in a plane or on a line.
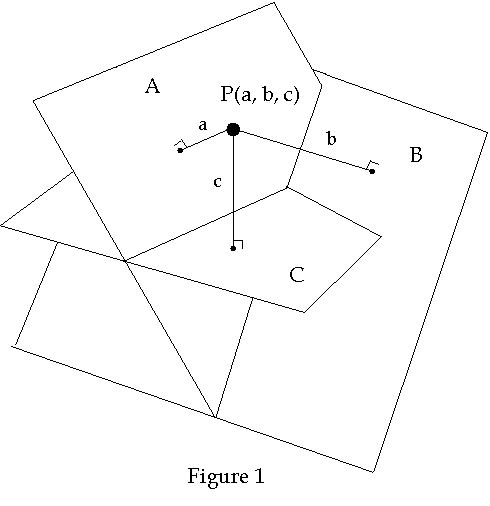
As example of a coordinate system in R3, consider three planes, called coordinate planes, each of which is not parallel to the other two planes. The distance along a perpendicular line from the point to each of the planes then uniquely locates the point in space. Each distance is then a coordinate and is assigned a number, a, b, and c. The sign of the number is then defined according to the side of the plane the point is located. Each plane is labeled so as to determine which number applies to which plane. An example of one such scheme is shown below in Figure 1.

One convention for labeling the planes is according to the coordinate that the plane represents. For example: Plane A consists of all points for which a = 0, I.e. A = {(a, b , c) | a = 0}. However we could just as well label the plane according to the two coordinates which vary over the plane. For example: The plane defined by a = 0 might be referred to as the bc-plane. The later convention is the one most often used when the planes are mutually perpendicular such as that shown in Figure 2 below
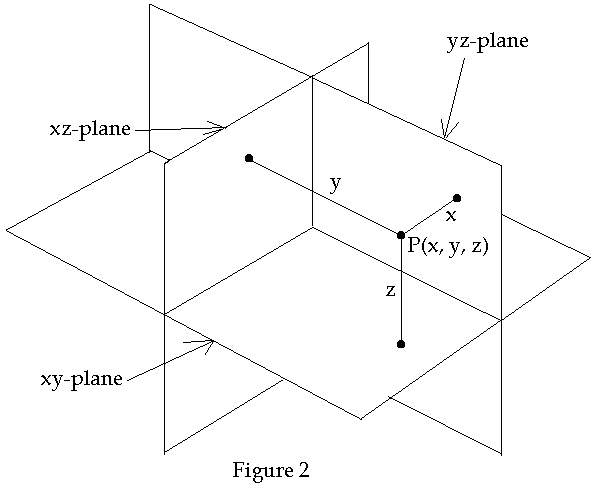
To simplify this diagram we construct three mutually perpendicular lines that each of which are the intersection of two planes. The x-axis consists of the intersection of the yz-plane and the xy-plane. Each of these lines is called a coordinate axis. Each point on each axis represents one coordinate of the point. The point where the lines intersect is called the origin of the coordinate system. See Figure 3.
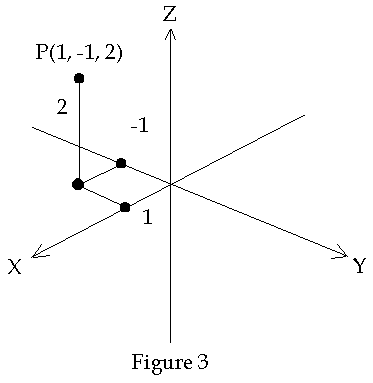
Each axis is divided into two portions, one on each side of the origin. Given a distance from the plane to the point there are two possibilities as to which side of the plane the point is located. In order to distinguish which side of the coordinate plane the point is on one assigns a "+" or "-" sign to the coordinate. In a diagram one normally places the label of the coordinate axis on the "+" portion of the coordinate axis. The most commonly used convention for these signs is shown in Figure 1.1.3. The xyz coordinate lines are oriented according to the right hand rule defined as follows: Hold out your right hand flat with the thumb pointed up and the palm facing left. Let the positive x-axis run normal to the palm. Let the positive y-axis run parallel to the fingers and let positive z-axis run parallel to the thumb. Such a coordinate system is called a Cartesian coordinate system. In Figure 1.1.3 the point P is shown as having coordinates (1, -1, 2). This illustrates one method of locating a point in R3. I.e. The intersection of three surfaces defines a point.
There are times when one is concerned only with points in a single plane. The plane will be referred to, in this section, as R2. Since the plane is a two dimensional space. Polar coordinates use one coordinate that is a distance and one that is an angle to define a point in the plane. See Figure 4.
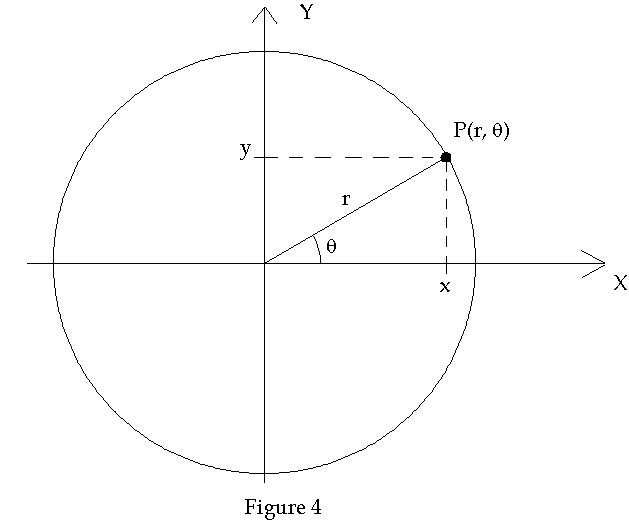
Notice that we could just as easily locate a point in the xy-plane with Cartesian coordinates P(x, y) as we could with polar coordinates P(r, q). The plane is usually referred to as the x-y plane even when polar coordinates are being used. The equations relating the two systems of coordinates are
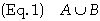
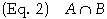
Similar to the polar coordinate system is the cylindrical coordinate system, for locating a point in R3, that has the coordinate r and q in the xy-plane but now has a z-coordinate to locate the point above or below the xy-plane. See Figure 5.
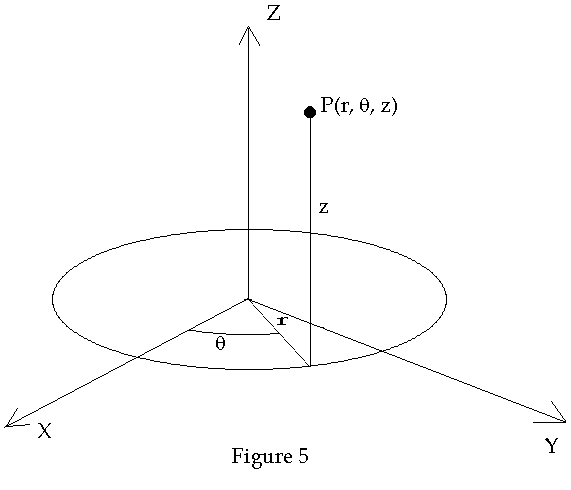
The equations relating the two cylindrical coordinates (r, q) to the two Cartesian coordinates (x, y) are given by Eq. 1.1.2. As mentioned above, a point can be uniquely determined by specifying three different surfaces, the point being located where the surfaces intersect. In the present case the point P(r, q, z) lies at the intersection of the infinite cylinder whose axis is the z axis, the plane which is parallel to the xy-plane and is located at a distance z from the xy-plane (above or below depending on whether z > 0 or z < 0 respectively) and the half plane which has one edge as the z axis and makes and angle q with the xz-plane.
In R3 a point may also be specified by using the spherical coordinate system which is defined using one distance coordinate and two angle coordinates as shown in Figure 6.
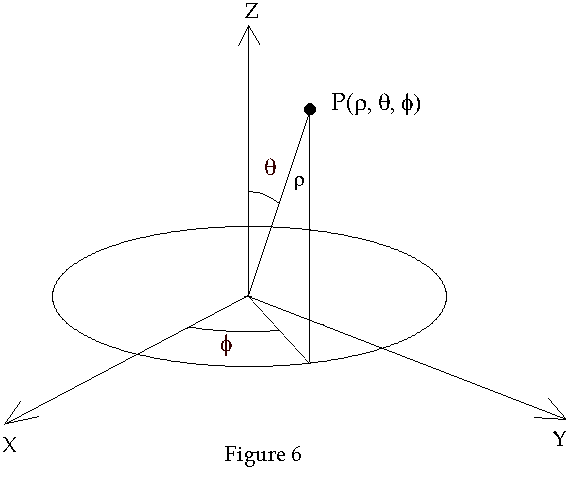
The equations relating spherical coordinates to Cartesian coordinates is given by
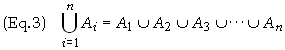
whereas the spherical coordinates are obtained by from the Cartesian coordinates by
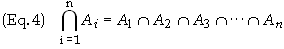
The surfaces corresponding to the three spherical coordinates are a sphere, corresponding to r, a cone corresponding to f and a plane corresponding to f. Note that if q = p /2 then the cone becomes a sphere.
Back
to GR Math
Back
to Physics World