Return to Index Ruunstabber unte Rächung Runes and Reckoning The Dythonic Runes and Numbering System
The Dythonic RunesThe following table shows the Dythonic Runes and their Latin alphabet equivalents. Although the runes have been invented, the font has not. I plan to offer a downloadable TrueType font here in the future for anyone's non-commercial use, once time permits me to create it. In the meantime, here are the runes: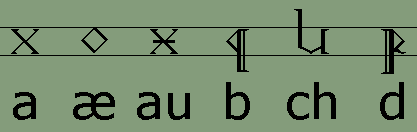 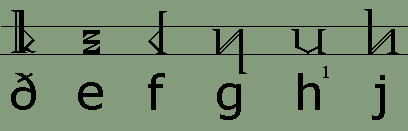 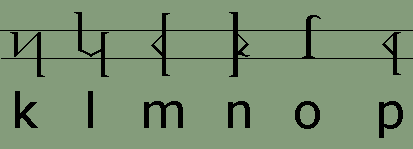 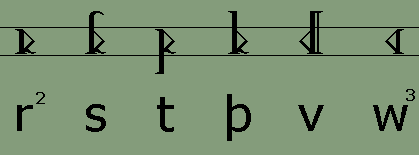 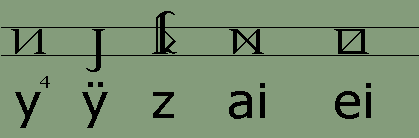
1. The rune for the semivocalic consonant h is used also for the vowel schwä. This vowel is usually transliterated into Latin script as an unstressed e. 2. The rune for the semivocalic consonant r is used also for the vowel ø. 3. The rune for the semivocalic consonant w is used also for the vowel u. 4. The rune for the semivocalic consonant y is used also for the vowel i. The rules for spelling Adelic words in the Latin alphabet (which can be found at this link) are different than those used in the Dythonic runes. In Dythonic writing, long vowels are always doubled, and the sounds of f and v are always written with their corresponding runes. For example, f never replaces v at the end of a word. Likewise, the Latin compound consonant ch is written in Dythonic with a single rune and is therefore doubled after a short vowel. Dythonic ReckoningMost people in our world use the number ten as the basis for counting. This is probably due to the fact that most of us learn to count on our ten fingers. There are exceptions to this, however. The ancient Mayan people of Central America based their counting on the number twenty, perhaps as a result of counting on their fingers and toes. There are myriad examples of systems that are not based on the number ten, especially when it comes to timekeeping. There are seven days in a week, four weeks to a month, four seasons in a year, twelve months in the year, twelve hours on the clock face, twelve periods in the zodiac, three hundred and sixty degrees in a circle, and probably others as well. That the number twelve was important in ancient times is given evidence by the fact that, in the Germanic languages at any rate, we don't start repeating number elements until after the number twelve. In other words, all of the numbers up to and including twelve have their own names, and once we reach thirteen, the names are compounds of the first nine plus "ten". The word "thirteen" consists of the elements "thir-" for three and "-teen" for ten. So why aren't there a "oneteen" and a "twoteen" after ten? For whatever mystical or religious reasons the number twelve was important enough for its own unique monicker despite the fact that it was "two left over" after counting to ten on one's fingers. For, of course, the literal meanings of the words eleven and twelve are "one left" and "two left" from the Germanic compounds "ain-lif" and "twa-lif." The Dythonic peoples have based their counting system on the number twelve since at least the time when their language split off from its Indo-European source. This means that instead of basing numbers on a system of ones, tens, hundreds, etc. the Dythonic system is built of ones, twelves, one hundred forty-fours, etc. That means the number 10 is not ten, but twelve - one set of twelve in the "twelves" column and zero single units in the "ones" column. Likewise, 20 is not twenty, but twenty-four - two sets of twelve in the "twelves" column and zero in the "ones" column. Going further, 125 is not one hundred twenty-five, but one hundred seventy-three - that is, one set of one hundred forty-four in the "144s" column plus two sets of twelve in the "twelves" column and five single units in the "ones" column. If none of this is making sense to you so far, I'll admit I'm not the best person to be teaching math subjects. What we're talking about here is base numbers and you might want to go to another site where base numbers are explained more clearly. One such site is the Math Doctor at http://forum.swarthmore.edu/dr.math/. Once one understands what counting in base twelve is all about, one realizes that our base ten numerals are not enough to work with, seeing as there are only ten of them, the numerals 0 through 9. To represent the numerals for ten and eleven we would have to substitute other symbols. One popular method is to use alphabetic characters, as in hexadecimals which are used in coding colors in html, the computer language used to write web pages, with which many surfers may be already familiar. But the Dythonic peoples, along with having their own runic alphabet, have their own runic numerals. And there are twelve of them as shown here:   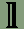    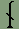 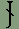 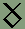   
Their names are nænne, ænne, ðwæ, drï, gwør, bimpe, sekke, sippe, aaþ, niif, ðekke, ælligg, and of course ðwællu as twelve which is represented by ænne followed by nænne like so: Here are some examples of what Dythonic numbers look like: The year 2000: 120: 365: 99: 143: The following table spells out Dythonic numbers along with the base ten equivalent. The last number, stiigratt, as 1212 is equivalent to our world's 1012 which is called, in America at least, one trillion - although 1212 is close to nine trillion in base ten.
And finally, just one more example:
Introduction | Grammar | Dictionary | Examples | Runes What's New | Rate this Page | Author's Home Page | Email Copyright © 1998-2000 S. A. MacLagan. All rights reserved. |