120 degree triples and 60 degree triples from Fibonacci numbers

Figure 2: 120 degree triangle

A 120 degree triple is a solution, $(a,b,c)$ , in positive integers to the 120 degree triangle equation

$$a^2+b^2-2ab\cos120^{ \circ}=a^2+b^2+ab = c^2.$$

If additionally $a, b$ ,and $c$ are pairwise relatively prime then $(a,b,c)$ is a primitive 120 degree triple.

$(a,b,c)$ is a primitive 120 degree triple if and only if there exists relative prime integers $u$ and $v$ , $u > v$ and $3\nmid u-v$ such that

$$a=u^2-v^2,\quad b=2uv+v^2, \quad c=u^2+v^2+uv.$$ (41)

See (8) for a proof.

For $n>2$ , the $n^{th}$ Fibonacci number is given by $F_n=F_{n-2}+F_{n-1}$ where $F_1=F_2=1$ . The first few are $1,1,2,3,5,8,13,21,34$ .

Some notation:

•     $(s,t)=d$ means that the positive integer $d$ is the greatest common divisor of the two integers $s$ and $t$ . If $d=1$ then $s$ and $t$ are relatively prime.
  
•     $s\mid t$ means $s$ divides $t$ .
  
•     $s\nmid t$ means $s$ does not divide $t$ .
  
•      $\Rightarrow$ means implies.

.

Claim 10   If $F_n, F_{n+1}, F_{n+2}, F_{n+3}$ , and $F_{n+4}$ are 5 consecutive Fibonacci numbers then

$$\Bigl(F_nF_{n+3}, F_{n+1}F_{n+4}, F_{n+1}F_{n+4}+F_nF_{n+2}\Bigr)$$

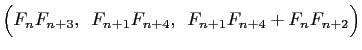
is a 120 degree triple. And if $\colorbox{Goldenrod}{\boxed{3\nmid F_n}}$ then it's a primitive triple. That is

$$(F_nF_{n+3})^2+(F_{n+1}F_{n+4})^2+(F_nF_{n+3})(F_{n+1}F_{n+4})=(F_{n+1}F_{n+4}+F_nF_{n+2})^2$$

where each side of the triangle is relatively prime to each of the other two sides.

Proof. First note that any two consecutive Fibonacci numbers are relatively prime.

Proof. This is true if $F_n=1.$ So assume $F_n>1.$ Let $d$ be an integer greater than zero. If $d\mid F_{n+1}=F_{n-1}+F_n$ and $d\mid F_{n}$ then $d\mid F_{n-1}+F_n - F_n =F_{n-1}.$ Similarly, since $d\mid F_n =F_{n-2}+F_{n-1}$ and $d\mid F_{n-1}$ then $d\mid F_{n-2}.$ Continue in this manner until it's found that $d\mid F_{n-(n-1)}=F_1=1.$ Thus, $\bigl(F_{n+1},F_n\bigr)=\bigl(F_{n+1},1\bigr)=1.$

Hence $F_{n+1}$ and $F_n$ are relatively prime. $\qedsymbol$

Let $v=F_{n+1}$ and $u=F_{n+2}$ . Then $3\nmid F_n\Rightarrow 3\nmid F_n+F_{n+1}-F_{n+1} =F_{n+2}-F_{n+1}=u-v$ . So, we have

1. $F_n=u-v$ .
2. $F_{n+1}=v$ .
3. $F_{n+2}=u$ .
4. $F_{n+3}=v+u$ .
5. $F_{n+4}=v+2u$ .

From equation (48),

$$a =u^2-v^2=(u-v)(u+v)=F_nF_{n+3},$$

$$b =2uv+v^2=v(v+2u)=F_{n+1}F_{n+4},$$

$$c =u^2+v^2+uv=v(v+2u)+(u-v)u=F_{n+1}F_{n+4}+F_nF_{n+2}.$$

$\qedsymbol$

Example

Let $F_n=5$ , then $F_{n+1}=8$ , $F_{n+2}=13$ , $F_{n+3}=21$ , and $F_{n+4}=34$ . So

$$F_nF_{n+3}= 5\cdot 21=105,$$

$$F_{n+1}F_{n+4}=8\cdot 34=272,$$

$$\quad F_{n+1}F_{n+4}+F_nF_{n+2}=8\cdot 34+5\cdot 13=337.$$

Then

$$105^2+272^2+105\cdot 272=337^2$$

.

This works for generalized Fibonacci numbers also. That is, choose any two positive integers $N_0$ and $N_1$ , then obtain integers $N_2, N_3$ , and $N_4$ thusly,

1. $N_0+N_1=N_2$ .
2. $N_1+N_2=N_3$ .
3. $N_2+N_3=N_4$ .

Set $N_1=v$ and $N_2=u$ . We have

1. $N_0=u-v$ .
2. $N_1=v$ .
3. $N_2=u$ .
4. $N_3=v+u$ .
5. $N_4=v+2u$ .

Then $(N_0N_3, N_1N_4, N_1N_4+N_0N_2)$ is a 120 degree triple.

Example: If $N_0=13$ and $N_1=1$ then $N_2=14, N_3=15$ , and $N_4=29$ . Therefore

$$(13\cdot 15)^2+(1\cdot 29)^2+(13\cdot 15)(1\cdot 29)=(1\cdot 29+13\cdot 14)^2.$$

Sixty degree triangles

Figure 3: 60 degree triangles

Construct equilateral triangles on each of the shorter legs of the $120^{ \circ}$ triangle in Figure (2) creating the two $60^{ \circ}$ triangles $ABD$ and $ACD$ as shown in figure (3). Thus,

$$\bigl(F_{n}F_{n+3}, F_{n}F_{n+3}+F_{n+1}F_{n+4}, F_{n+1}F_{n+4}+F_nF_{n+2}\bigr)$$

$$\quad \bigl(F_{n}F_{n+3}+F_{n+1}F_{n+4}, F_{n+1}F_{n+4}, F_{n+1}F_{n+4}+F_nF_{n+2}\bigr)$$

are $60^{ \circ}$ triples. That is,

$$(F_{n}F_{n+3})^2+(F_{n}F_{n+3}+F_{n+1}F_{n+4})^2-(F_{n}F_{n+3})(F_{n}F_{n+3}+F_{n+1}F_{n+4})$$

$$= (F_{n}F_{n+3}+F_{n+1}F_{n+4})^2+(F_{n+1}F_{n+4})^2-(F_{n}F_{n+3}+F_{n+1}F_{n+4})(F_{n+1}F_{n+4})$$

$$= (F_{n+1}F_{n+4}+F_nF_{n+2})^2.$$

Download this section: fibo.pdf or fibo.ps

Hosted by www.Geocities.ws