Download Deriving 120 degree and 60 degree triples.
triples10.pdf
A 120 degree triple ![]() is a solution in positive integers
to the equation
is a solution in positive integers
to the equation
If, additionally, ![]() , and
, and ![]() are pairwise relatively prime
then
are pairwise relatively prime
then ![]() is a primitive 120 degree triple, and
is a primitive 120 degree triple, and
![]() is a primitive 120 degree triangle. Clearly, if
some integer
is a primitive 120 degree triangle. Clearly, if
some integer ![]() divides any two of the variables
divides any two of the variables ![]() ,
, ![]() , and
, and ![]() then it divides the remaining variable, therefore
then it divides the remaining variable, therefore ![]() can be divided
out. Similarly, if
can be divided
out. Similarly, if ![]() is primitive then multiply through by
the appropriate integer to get your chosen non-primitive solution.
Hence, to find all solutions, it's sufficient to find all primitive
solutions.
is primitive then multiply through by
the appropriate integer to get your chosen non-primitive solution.
Hence, to find all solutions, it's sufficient to find all primitive
solutions.
We will need a preliminary result.
where
Let
![]() be a primitive 120 degree triangle. From the
triangle inequality, and since
be a primitive 120 degree triangle. From the
triangle inequality, and since ![]() and
and ![]() are each non-zero,
the sum of the lengths of any two sides is greater than the length
of the remaining side. That is,
are each non-zero,
the sum of the lengths of any two sides is greater than the length
of the remaining side. That is, ![]() . Therefore, there exists
relatively prime positive integers
. Therefore, there exists
relatively prime positive integers ![]() and
and ![]() ,
, ![]() , such that
, such that
Thus
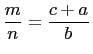
reduced to lowest terms. From whence
Square both sides of (29), multiply through by ![]() , then
cancel and rearrange terms to get the result,
, then
cancel and rearrange terms to get the result,
There are two cases,
![]() and
and ![]() .
.
Case I,
![]() . From Lemma (1),
. From Lemma (1),
![]() . Also
. Also ![]() . Thus, from
(30),
. Thus, from
(30),
| (31) |
Case II,
![]() . From Lemma
(1),
. From Lemma
(1),
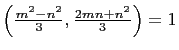 .
Then, from (30),
.
Then, from (30),
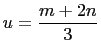 and
and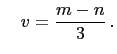
Then
Substituting these values for
Therefore, all 120 degree triples where ![]() is considered the
same as
is considered the
same as ![]() are given by the parametric equations,
are given by the parametric equations,
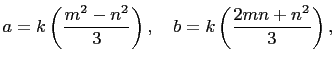 and
and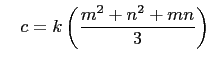
for some positive integer
Let
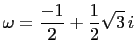 and
and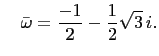
Then
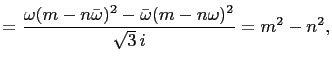 |
||
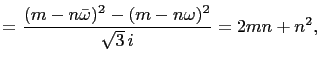 |
||
| and |
If ![]() , and
, and ![]() are positive integers such that
are positive integers such that
![]() then
then ![]() is a 60 degree triple. If additionally
is a 60 degree triple. If additionally ![]() ,and
,and
![]() are pairwise relatively prime then
are pairwise relatively prime then ![]() is a primitive 60
degree triple. If
is a primitive 60
degree triple. If ![]() is a primitive 60 degree triple then
is a primitive 60 degree triple then
![]() is a primitive 60 degree triangle, and vice versa.
is a primitive 60 degree triangle, and vice versa.
Parametric equations for finding all 60 degree triples can be easily derived from the parametric equations for finding all 120 degree triples. (34)
First note that for any positive integer ![]() ,
, ![]() is a 60
degree triple. That is,
is a 60
degree triple. That is,
![]() where
where ![]() is the length of
each side of an equilateral triangle. Clearly, if
is the length of
each side of an equilateral triangle. Clearly, if ![]() is a 60
degree triple where
is a 60
degree triple where ![]() then
then ![]() . So, since we already know how
to write down the side lengths of an equilateral triangle, the
triples such that
. So, since we already know how
to write down the side lengths of an equilateral triangle, the
triples such that ![]() need not be included in our derivation.
need not be included in our derivation.
And in the other direction,
![]() .
.
And in the other direction,
![]()
From equation (34) and Claim (7), where
![]() and
and
![]() , if
, if ![]() ,
,
![]() is a 60 degree triple if and only if there exists
relatively prime positive integers,
is a 60 degree triple if and only if there exists
relatively prime positive integers,![]() and
and ![]() ,
,
![]() , and
, and
![]() such that
such that
or
Where
Figure (1) illustrates Claim (7) where in
![]() and
and ![]() , and in
, and in
![]() and
and ![]() .
.