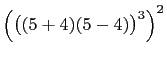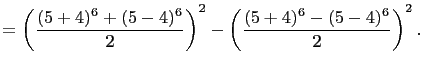


Next: Finding m and n
Up: Pythagorean Triples, etc.
Previous: Pythagorean Triples, etc.
Contents
This section in pdf form. triples2.pdf
If 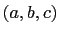 is a positive integer solution to the equation
is a positive integer solution to the equation
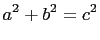 |
(1) |
then 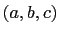 is a Pythagorean triple. If
is a Pythagorean triple. If 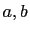 , and
, and 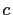 have no
common divisors greater than
have no
common divisors greater than 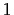 , then
, then 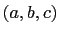 is a primitive
Pythagorean triple (PPT). Similarly, if
is a primitive
Pythagorean triple (PPT). Similarly, if
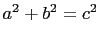 where
where
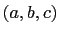 is a PPT then
is a PPT then
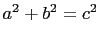 is primitive. In the
following list only the second triangle is not primitive.
is primitive. In the
following list only the second triangle is not primitive.
-
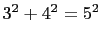
-
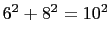
-
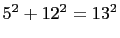
-
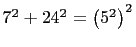
-
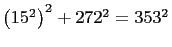
Clearly, if 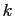 divides any two of
divides any two of 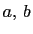 ,
and
,
and 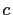 it divides all three. And if
it divides all three. And if
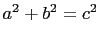 then
then
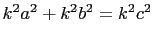 . That is, for a positive integer
. That is, for a positive integer 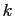 , if
, if
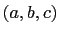 is a Pythagorean triple then so is
is a Pythagorean triple then so is
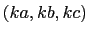 . Hence,
to find all Pythagorean triples, it's sufficient to find all
primitive Pythagorean triples.
. Hence,
to find all Pythagorean triples, it's sufficient to find all
primitive Pythagorean triples.
Let 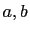 , and
, and 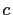 be relatively prime positive integers such
that
be relatively prime positive integers such
that
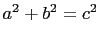 . Set
. Set
reduced to
lowest terms, That is,
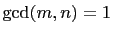 . From the triangle inequality
. From the triangle inequality
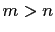 . Then
. Then
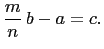 |
(2) |
Squaring both sides of (2) and multiplying through by
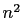 we get
we get
which, after canceling and rearranging terms, becomes
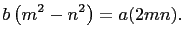 |
(3) |
There are two cases, either 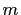 and
and 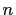 are of opposite parity, or
they or both odd. Since
are of opposite parity, or
they or both odd. Since
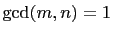 , they can not both be
even.
, they can not both be
even.
Case 1. 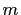 and
and 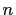 of opposite parity, i.e.,
of opposite parity, i.e.,
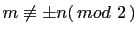 . So 2 divides b since
. So 2 divides b since
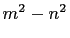 is odd. From equation (2),
is odd. From equation (2), 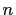 divides
divides 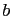 .
Since
.
Since
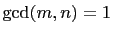 then
then
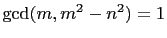 , therefore
, therefore 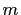 also
divides
also
divides 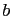 . And since
. And since
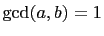 ,
, 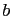 divides
divides 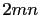 . Therefore
. Therefore
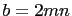 . Then
. Then
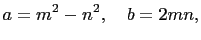 and from (2) and from (2) |
(4) |
Case 2. 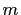 and
and 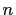 both odd, i.e.,
both odd, i.e.,
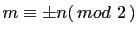 . So 2 divides
. So 2 divides 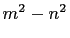 . Then by the same process
as in the first case we have
. Then by the same process
as in the first case we have
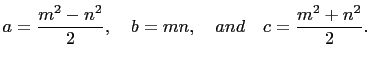 |
(5) |
The parametric equations in (4) and (5) appear
to be different but they generate the same solutions. To show
this, let
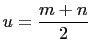
and
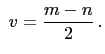
Then 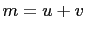 , and
, and 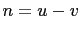 . Substituting those values for
. Substituting those values for 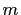 and
and
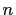 into (5) we get
into (5) we get
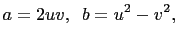 and and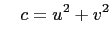 |
(6) |
where 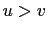 ,
,
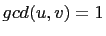 , and
, and 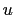 and
and 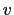 are of opposite parity.
Therefore (6), with the labels for a and b interchanged,
is identical to (4). Thus since
are of opposite parity.
Therefore (6), with the labels for a and b interchanged,
is identical to (4). Thus since
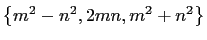 , as in (4), is a
primitive Pythagorean triple, we can say that
, as in (4), is a
primitive Pythagorean triple, we can say that 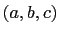 is a
primitive pythagorean triple if and only if there exists relatively
prime, positive integers
is a
primitive pythagorean triple if and only if there exists relatively
prime, positive integers 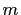 and
and 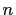 ,
, 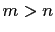 , such that
, such that
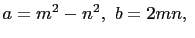 and
and 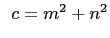 . And
. And
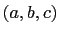 is a Pythagorean triple if and only if
is a Pythagorean triple if and only if
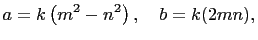
and
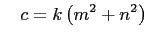
where 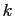 is a positive integer.
is a positive integer.
Alternatively, 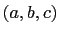 is a Pythagorean triple if and only if
there exists relatively prime, positive integers
is a Pythagorean triple if and only if
there exists relatively prime, positive integers 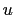 and
and 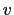 ,
, 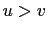 ,
,
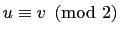 such that
such that
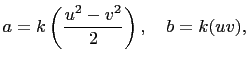
and
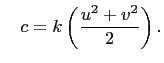
Another Method (using Gaussian Integers).
Let
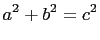 |
(7) |
where 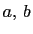 , and
, and 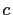 are pairwise, relatively prime, positive
integers. Let
are pairwise, relatively prime, positive
integers. Let 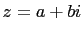 and
and
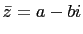 , where
, where
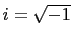 .
Then
.
Then 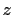 and
and 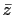 are Gaussian Integers, and
are Gaussian Integers, and 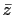 is the
conjugate of
is the
conjugate of 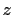 . Note that
. Note that
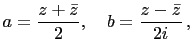 and and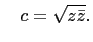 |
(8) |
Since
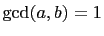 then
then
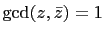 . Hence each of
. Hence each of 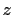 and
and
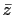 is a square. That is, there exists integers
is a square. That is, there exists integers 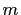 and
and 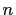 such that
such that
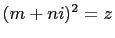 and
and
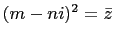 . So, from equation
(8),
. So, from equation
(8),
Since 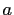 is a positive integer,
is a positive integer, 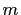 and
and 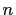 must be positive
integers,
must be positive
integers, 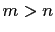 . And since
. And since
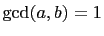 ,
, 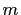 and
and 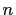 must be
relatively prime and of opposite parity.
must be
relatively prime and of opposite parity.
Equation (8) illustrates a method for finding primitive
Pythagorean triangles where the hypotenuse is to a power. We have
the identity,
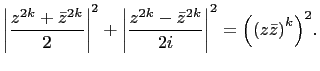 |
(9) |
The absolute values are necessary since the terms on the left,
depending on 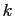 , may, or may not, be positive.
, may, or may not, be positive.
Example
Let 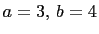 , and
, and 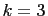 . Then, from equation (9), we
have,
. Then, from equation (9), we
have,
Still another method -- the difference method.
Let 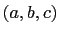 be a primitive Pythagorean triple. Without loss of
generality, let
be a primitive Pythagorean triple. Without loss of
generality, let 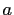 be odd. Equation (7) can be written
as,
be odd. Equation (7) can be written
as,
Set 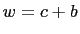 and
and
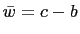 . Thus,
. Thus,
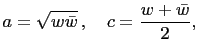 and and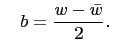 |
(10) |
Since 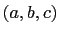 is primitive,
is primitive,
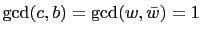 . This
implies that each of
. This
implies that each of 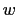 and
and 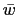 is a square. So, since any
odd positive integer greater than 1 can be written as the difference
of two positive integer squares, there exists positive integers
is a square. So, since any
odd positive integer greater than 1 can be written as the difference
of two positive integer squares, there exists positive integers 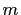 and
and 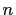 ,
, 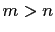 , such that
, such that 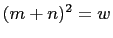 and
and
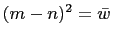 . Hence,
from equation (10),
. Hence,
from equation (10),
And, since
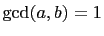 ,
, 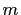 and
and 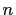 must be relatively prime and
of opposite parity.
must be relatively prime and
of opposite parity.
Equation (10) illustrates an efficient method for finding
primitive Pythagorean triples where the odd leg is to a power. We
have the identity,
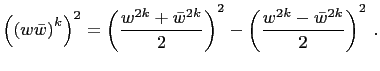 |
(11) |
Example
Let
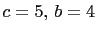 , and
, and 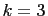 . Then, from equation (11), we
have,
. Then, from equation (11), we
have,



Next: Finding m and n
Up: Pythagorean Triples, etc.
Previous: Pythagorean Triples, etc.
Contents
f. barnes
2008-04-29
![\includegraphics[width=1.5in]{../../../texdocs/ip1}](img9.gif)
![\includegraphics[width=1.5in]{../../../texdocs/ip1}](img9.gif)
![]() is a positive integer solution to the equation
is a positive integer solution to the equation
![]() divides any two of
divides any two of ![]() ,
and
,
and ![]() it divides all three. And if
it divides all three. And if
![]() then
then
![]() . That is, for a positive integer
. That is, for a positive integer ![]() , if
, if
![]() is a Pythagorean triple then so is
is a Pythagorean triple then so is
![]() . Hence,
to find all Pythagorean triples, it's sufficient to find all
primitive Pythagorean triples.
. Hence,
to find all Pythagorean triples, it's sufficient to find all
primitive Pythagorean triples.
![]() , and
, and ![]() be relatively prime positive integers such
that
be relatively prime positive integers such
that
![]() . Set
. Set
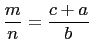
![]() and
and ![]() of opposite parity, i.e.,
of opposite parity, i.e.,
![]() . So 2 divides b since
. So 2 divides b since
![]() is odd. From equation (2),
is odd. From equation (2), ![]() divides
divides ![]() .
Since
.
Since
![]() then
then
![]() , therefore
, therefore ![]() also
divides
also
divides ![]() . And since
. And since
![]() ,
, ![]() divides
divides ![]() . Therefore
. Therefore
![]() . Then
. Then
![]() and
and ![]() both odd, i.e.,
both odd, i.e.,
![]() . So 2 divides
. So 2 divides ![]() . Then by the same process
as in the first case we have
. Then by the same process
as in the first case we have
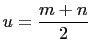 and
and 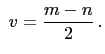
![]() is a Pythagorean triple if and only if
there exists relatively prime, positive integers
is a Pythagorean triple if and only if
there exists relatively prime, positive integers ![]() and
and ![]() ,
, ![]() ,
,
![]() such that
such that
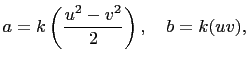 and
and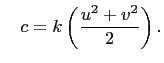
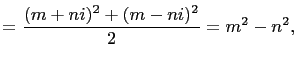
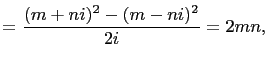
![]() , and
, and ![]() . Then, from equation (9), we
have,
. Then, from equation (9), we
have,
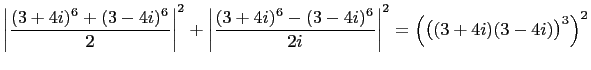
![]() be a primitive Pythagorean triple. Without loss of
generality, let
be a primitive Pythagorean triple. Without loss of
generality, let ![]() be odd. Equation (7) can be written
as,
be odd. Equation (7) can be written
as,
![]() and
and
![]() . Thus,
. Thus,
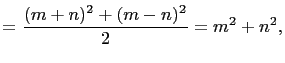
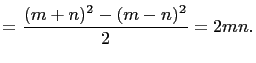
![]() , and
, and ![]() . Then, from equation (11), we
have,
. Then, from equation (11), we
have,