This section in pdf form. triples11.pdf
Usually when people speak of multiplying Pythagorean triples they
are referring to multiplying the hypotenuses of of two triples to
generate another Pythagorean triple. For example, if
![]() and
and
![]() are Pythagorean triples then
are Pythagorean triples then
![]() is also a Pythagorean
triple. However, Pythagorean triples can be generated by multiplying
the other sides of two triples as well. That is, not only does
is also a Pythagorean
triple. However, Pythagorean triples can be generated by multiplying
the other sides of two triples as well. That is, not only does
![]() generate a Pythagorean triple, so does
generate a Pythagorean triple, so does
![]() and
and ![]()
We will first derive identities for multiplying the sums of two squares and for multiplying the differences of two squares to give the sum of two squares and the difference of two squares respectively.
Let
![]() and
and
![]() be elements of an
integral domain. Then,
be elements of an
integral domain. Then,
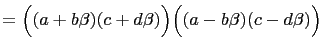 |
||
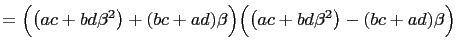 |
||
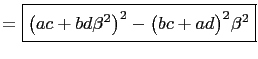 |
||
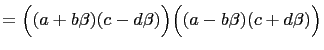 |
||
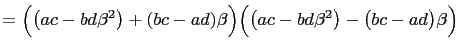 |
||
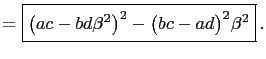 |
Hence, we have
Set
![]() and substitute into equation (24)
to get Fibonacci's Identity for multiplying the sums of two squares,
and substitute into equation (24)
to get Fibonacci's Identity for multiplying the sums of two squares,
Set ![]() , to get the Diophantus identity for multiplying the
differences of two squares,
, to get the Diophantus identity for multiplying the
differences of two squares,
Each of these identities is a special case of Brahmagupta's identity,
Set ![]() and
and ![]() in (27) to get equations (25) and
(26) respectively.
in (27) to get equations (25) and
(26) respectively.
Note that
![]() ,
,
![]() , and
, and
![]() are
equivalent methods of writing a Pythagorean triangle.
are
equivalent methods of writing a Pythagorean triangle.
If
![]() and
and
![]() are two Pythagorean triples
then, from equations(25) and (26), we have
are two Pythagorean triples
then, from equations(25) and (26), we have
From which we will define the following multiplications where
![]() and
and
![]() are Pythagorean triples. And
the over bars designate multiplier and multiplicand.
are Pythagorean triples. And
the over bars designate multiplier and multiplicand.
If
![]() and
and ![]() then, from items
then, from items
![]() ,
,
The ordered triples ![]() and
and ![]() are Pythagorean
triples, hence from
are Pythagorean
triples, hence from ![]() , we get the resultant Pythagorean
triples,
, we get the resultant Pythagorean
triples,
Let ![]() be odd. Then clearly, from items i through v, if
be odd. Then clearly, from items i through v, if ![]() is a primitive Pythagorean triple (PPT) then so are
is a primitive Pythagorean triple (PPT) then so are
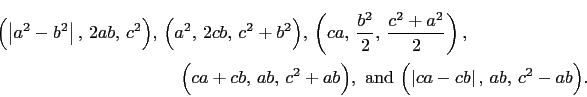
Example: Since ![]() is a PPT, so are
is a PPT, so are
![$\displaystyle \left[ \begin{matrix}a_1 & b_1 & c_1\end{matrix}\right]
\left[\begin{matrix}a_2\ b_2\ c_2\end{matrix}\right] =
a_1a_2+b_1b_2+c_1c_2
$](img493.gif)
is a perfect square.
Where
Hence we have,
Similarly it can be shown that the sums
![]() ,
,
![]() , and
, and
![]() are also
perfect squares.
are also
perfect squares.
![]()
Example: Let ![]() be a PPT where a is
even, then each of the sums
be a PPT where a is
even, then each of the sums
![]() and
and
![]() is
a perfect square.
is
a perfect square.
Case 1, ![]() is even: So, there exists
relatively prime positive integers of opposite parity,
is even: So, there exists
relatively prime positive integers of opposite parity, ![]() and
and ![]() ,
, ![]() , such that
, such that
where 3 divides exactly one of
If ![]() , set
, set ![]() equal to the greater of
equal to the greater of ![]() and
and ![]() and
and ![]() equal to the lesser. Then choose
equal to the lesser. Then choose ![]() and
and ![]() such that
such that
Then we have
Case 1a, ![]() :
:
And since
Case 1b, ![]() :
:
Where
Case 2, ![]() is odd: So, there exists
relatively prime positive integers of opposite parity,
is odd: So, there exists
relatively prime positive integers of opposite parity, ![]() and
and ![]() ,
, ![]() , such that
, such that
Note that since ![]() and
and ![]() are relatively prime then so are
are relatively prime then so are ![]() and
and ![]() .
.
Case 2a, 3 divides ![]()
set
![]() and
and
![]() Then
choose
Then
choose ![]() and
and ![]() such that
such that
We have,
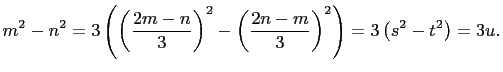 |
||
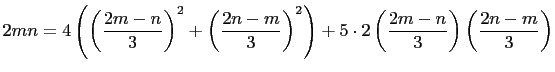 |
||
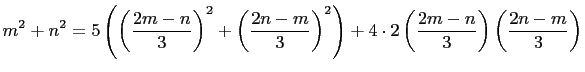 |
||
Case 2b, 3 divides ![]() set
set
![]() and
and
![]() Then choose
Then choose ![]() and
and ![]() such that
such that
We have,
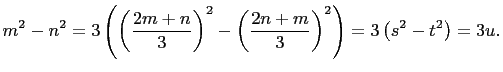 |
||
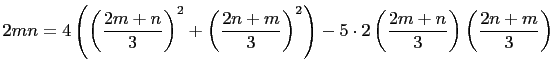 |
||
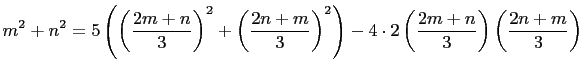 |
||
And going in the other direction, if ![]() is a PPT then either
is a PPT then either
![]() or
or
![]() is a PPT.
is a PPT.
Similarly, if
![]() then
then ![]() or
or ![]() . That
is,
. That
is,
![]() and
and
![]() . This
implies that
. This
implies that ![]() and
and ![]() , a contradiction. Hence either
, a contradiction. Hence either
![]() or
or
![]() is primitive.
is primitive.
![]()
That is, if
![]() divides
divides
![]() then
then
![]() is a primitive Pythagorean triple if and only if
there exists a primitive Pythagorean triple
is a primitive Pythagorean triple if and only if
there exists a primitive Pythagorean triple
![]() such
that
such
that
![]() and
and
![]() are primitive Pythagorean
triples where 3 divides the even side.
are primitive Pythagorean
triples where 3 divides the even side.
Problem 1: Find a PPT ![]() such that
such that
Solution: Since
![]() is primitive,
is primitive,
![]() (reduced to lowest terms) equals
(reduced to lowest terms) equals ![]() . (see
Finding
. (see
Finding ![]() and
and ![]() ... )
So
... )
So
![]() and
and ![]() . Then
. Then
And
Similarly, since
![]() is primitive,
is primitive,
![]() So
So ![]() and
and ![]() . Since
. Since
![]() , we have
, we have
![]() is a PPT where 3 divides the odd side.
is a PPT where 3 divides the odd side.
Problem 2: Find a PPT ![]() such that
such that
![]()
Solution: Since
![]() is a PPT,
is a PPT,
![]() And 3 divides
And 3 divides
![]() ,
therefore
,
therefore
![]() and
and
![]() So,
So,