Prefacio
Del prefacio del autor a la tercera edici�n rusa
1. La quinta operaci�n matem�tica
2. El idioma del �lgebra
3. En ayuda de la aritm�tica
4. Las ecuaciones de Diofanto
5. La sexta operaci�n matem�tica
6. Ecuaciones de segundo grado
7. La magnitud mayor y la menor
8. Progresiones
9. La s�ptima operaci�n matem�tica
Bajar Documento Completo

Capitulo S�ptimo
LA MAGNITUD MAYOR Y LA MENOR
Contenido
1. Dos trenes
2. �D�nde construir el apeadero?
3. �C�mo trazar la carretera al embarcadero?
4. �Cu�ndo alcanza el producto su m�ximo valor?
5. �Qu� suma ser� la menor?
6. El tronco de mayor volumen
7. Dos parcelas de tierra
8. La cometa
9. La construcci�n de una casa
10. La parcela
11. El canal�n de secci�n m�xima
12. El embudo de mayor capacidad
13. La iluminaci�n m�s intensa
Los problemas presentados en este cap�tulo pertenecen a una clase muy interesante; con ellos se propone hallar el valor mayor o el menor de cierta magnitud. Estos problemas pueden ser resueltos por diferentes procedimientos, uno de los cuales exponemos a continuaci�n.
P. Chebyshev, matem�tico ruso, en su obra "Delineaci�n de los mapas geogr�ficos" escrib�a que los m�todos, que ayudaban a resolver un problema com�n para toda la actividad pr�ctica del hombre - c�mo disponer de sus medios para obtener, en la medida de lo posible, mayor provecho tienen una importancia especial.
1. Dos trenes
Problema
Dos l�neas f�rreas se cruzan formando un �ngulo recto. Los trenes se acercan a gran velocidad hacia el cruce. Uno parte de cierta estaci�n situada a 40 km del cruce; el otro, de una estaci�n que dista 50 km del cruce. El primero marcha a una velocidad de 800 m por minuto, el segundo a 600 m �Cu�ntos minutos transcurrir�n desde el momento de la partida para que las locomotoras se hallen a la menor distancia entre s�, y cu�l ser� esa distancia?
Soluci�n
Dibujemos el esquema de la marcha de los trenes. Supongamos que las l�neas rectas AB y CD son dos l�neas f�rreas que se cruzan (fig. 19 . ) La estaci�n B se encuentra a 40 km del cruce O , y la estaci�n, D a 50 km. Admitamos que al cabo de x minutos los trenes se encuentran a la distancia m�s pr�xima entre s�: (MN = m). El tren que sale de B hace el recorrido BM = 0,8 x , ya que en un minuto recorre 800 m = 0,8 km. Por consiguiente, OM = 40 - 0,8 x . Del mismo modo hallaremos que ON = 50 - 0,6 x . Seg�n el teorema de Pit�goras
Elevemos al cuadrado ambas partes de la ecuaci�n
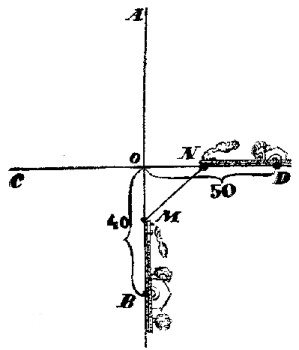
|
| Figura 19. |
Resolviendo la ecuaci�n para hallar el valor de x , resultar�
Ya que x , el n�mero que expresa los minutos transcurridos, no puede ser una ra�z imaginaria, entonces m 2 -256 debe ser una magnitud positiva o, a llo sumo, equivalente a cero. El �ltimo es el que corresponde al valor m�nimo de m; de aqu� que:
Es evidente que m no puede ser menor que 16, de lo contrario x se convertir�a en una ra�z imaginaria. Y si m 2 � 256 = 0, entonces x = 62.
De esta forma las locomotoras llegan a su punto de mayor aproximaci�n al cabo de 62 minutos, y la distancia que las separa ser� de 16 km. Determinemos d�nde se encontrar� cada una en el momento de mayor aproximaci�n. Al buscar la distancia OM, tendremos que es igual a
El signo negativo indica que la primera locomotora habr� rebasado el cruce en 9,6 km. La distancia ON ser�:
Es decir, que a la segunda locomotora le faltar�n 12,8 km para llegar al cruce. En la fig. 20 se ve la posici�n que ocupan las locomotoras en el momento dado. Se puede apreciar que �sta no es tal y como nos la imagin�bamos al principio.
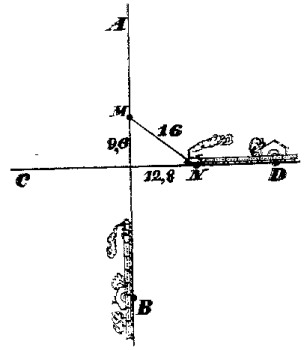
|
| Figura 20. |
La ecuaci�n ha resultado ser tan tolerante que, a pesar de lo err�neo del esquema, nos da un resultado acertado. No es dif�cil averiguar de d�nde proviene esa tolerancia, que est� condicionada por las reglas algebraicas de los signos.
Volver
2. �D�nde construir el apeadero?
Problema
A 20 km del ferrocarril, cuya l�nea es recta, se encuentra el punto poblado B (fig. 21).
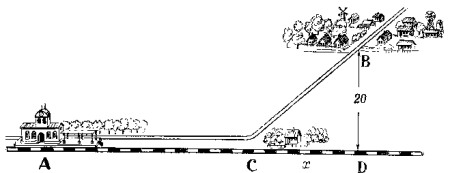
|
| Figura 21 |
�D�nde hay que construir el apeadero C para que en el viaje de A a B por la l�nea f�rrea AC, y por la carretera CB se invierta el menor tiempo posible? La velocidad por ferrocarril es de 0,8 y por carretera de 0,2 kil�metros por minuto.
Soluci�n
Expresemos la distancia AD (desde A hasta la base de la perpendicular BD a la horizontal AD ) con la a; y CD, con la x . Entonces
El tiempo empleado por el tren para cubrir el trayecto AC ser� igual a
El tiempo necesario para recorrer la distancia CB de la carretera equivale a
El viaje desde A hasta B ocupar�, en total,
Esta suma, que expresamos con m, debe ser la menor.
La ecuaci�n
pres�ntase as�:
Multiplicando por 0,8 tendremos
Y cuando expresamos 0,8 m - a , con la k , haciendo desaparecer el radical, tendremos la ecuaci�n de segundo grado
de donde
Y como k = 0, 8 m - a, al alcanzar m la m�nima magnitud sucede lo mismo con la k, y viceversa. Mas para que x resulte real es necesario que 16 k 2 no sea menor que 96 000. Por lo tanto, el valor m�nimo para 16 k 2 ser� 96 000. Por esa raz�n, m ser� la magnitud menor cuando 116 k 2 = 96000,
de donde
y por consiguiente
El apeadero debe construirse aproximadamente a 5 km del punto D cualquiera sea la longitud a = AD.
No obstante, es evidente que nuestra soluci�n tiene sentido s�lo en el caso de x < a, pues al formular la ecuaci�n hemos considerado que la expresi�n a - x era un valor positivo.
Si x = a » 5,16 no hace falta ning�n apeadero y debe llevarse la carretera hasta la estaci�n. De manera id�ntica hay que operar en los casos en que la distancia a sea inferior a 5,16 km.
Esta vez somos nosotros los que hemos obrado con mayor prudencia que la ecuaci�n. Si hubi�ramos confiado ciegamente en la ecuaci�n, habr�amos tenido que construir el apeadero m�s all� de la estaci�n, cosa totalmente absurda: en este caso x>a, por eso, el tiempo a-x/ 0,8
durante el cual ten�amos que viajar en ferrocarril, ser�a negativo. El caso es aleccionador y muestra que, al valerse de recursos matem�ticos hay que mantener una actitud prudente hacia los resultados obtenidos, recordando siempre que si no se cumplen las condiciones en las que se fundamenta el empleo del recurso matem�tico, el resultado puede perder todo sentido.
Volver
3. �C�mo trazar la carretera al embarcadero?
Problema
Desde la ciudad ribereña A hay que trasladar cargamento al punto B, situado a a km m�s abajo, y a d km de la orilla del r�o (fig. 22).
�C�mo debe trazarse la carretera desde B al r�o para que el transporte de cargas desde A hasta B resulte lo m�s barato posible, considerando que el transporte de una tonelada-kil�metro por r�o cuesta la mitad que por carretera?
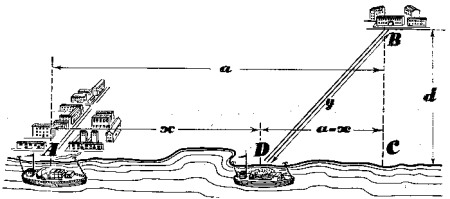
|
| Figura 22 |
Soluci�n
Expresaremos la distancia AD con la x, y la longitud de la carretera DB con la y . Como hemos supuesto, la longitud AC = a, y la BC = d. Puesto que el transporte por carretera cuesta el doble que por r�o, la suma
debe ser, respondiendo a las exigencias del problema, la m�s pequeña. Expres�mosla con la m . De aqu� la ecuaci�n
y
entonces la ecuaci�n se presentar� as�:
y, al hacer desaparecer el radical, resulta:
Resolvamos ahora la ecuaci�n:
Para que y responda a las condiciones, ( m - a ) 2 no debe ser inferior a 3 d 2 . La magnitud m�s pequeña de ( m - a ) 2 es igual a 3 d 2 y entonces

es decir,
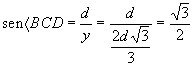
Mas el �ngulo cuyo seno es igual a Ö 3/2 equivale a 60�. Esto significa que la carretera debe ser trazada formando un �ngulo de 60� con el r�o, independiente de la distancia AC.
Aqu� vuelve a aparecer la misma particularidad que en el problema anterior. El resultado tiene sentido s�lo en determinadas condiciones. Si el punto poblado est� situado de tal manera que la carretera (cuya l�nea forma un �ngulo de 60� con la del r�o) pasa por el lado opuesto de la ciudad A, entonces la soluci�n dada es inaplicable; en este caso hay que unir directamente el punto B con la ciudad A por carretera sin emplear en absoluto el r�o para el transporte.
Volver
4. �Cu�ndo alcanza el producto su m�ximo valor?
Problema
Para resolver muchos problemas relacionados con "el m�ximo y el m�nimo", es decir, para buscar el valor mayor y el menor de una magnitud variable, puede emplearse un teorema algebraico que examinaremos a continuaci�n. Veamos el problema siguiente:
�En qu� dos partes debe dividirse un n�mero para que su producto alcance el m�ximo valor?
Soluci�n
Supongamos que el n�mero dado sea a . Las partes en que se divide a son
El n�mero x indica la diferencia de estas partes con la mitad de a. El producto de ellas es igual a
Es evidente que el producto de las partes tomadas aumentar� en la medida en que disminuya x , es decir, en la medida en que disminuya la diferencia entre las mismas. El resultado mayor ser� cuando x = 0, es decir, cuando ambas partes sean iguales a a /2
Quedarnos, pues, en que el n�mero debe dividirse por la mitad. El producto de dos n�meros, cuya suma sea constante alcanzar� su m�ximo valor cuando estos n�meros sean iguales entre s�.
Examinemos este mismo ejemplo con tres n�meros.
Problema
�En qu� tres partes debe dividirse un n�mero para que su producto alcance el m�ximo valor?
Soluci�n
Para resolver este problema nos apoyaremos en el anterior.
Tomemos un n�mero a dividido en tres partes. Supongamos previamente que ninguna de las tres partes es igual a a / 3- Entre ellas habr� una parte mayor que a / 3 (las tres no pueden ser menores que a / 3). Dicha parte la expresaremos as�:
Tambi�n habr� otra parte menor que a /3 que representaremos con
Los n�meros x e y son positivos. La parte tercera ser� indudablemente igual a
es mayor que el producto de las dos primeras partes del n�mero a .
De esta forma, si las dos primeras partes del n�mero a son sustituidas por los n�meros
dejando la tercera intacta, el producto aumentar�.
Supongamos ahora que una de las partes es igual a a /3 . Entonces las otras dos partes se presentar�n as�
Si hacemos que estas dos partes sean iguales a a /3 (cuya suma, por ello, no se altera), veremos que su producto aumenta, siendo igual a:
As� pues, si el n�mero a se divide en tres partes desiguales, el producto de �stas ser� menor que a 3 /27 es decir, menor que el producto de tres factores iguales que sumen a .
Por el mismo procedimiento puede demostrarse este teorema para cuatro factores, para cinco, etc.
Examinemos ahora un caso m�s general.
Problema
H�llese el valor de x y de y para que la expresi�n x p *y q alcance la mayor magnitud si x+ y = a.
Soluci�n
Busquemos el valor de x mediante el cual la expresi�n
alcance su m�xima magnitud.
Multipliquemos esta expresi�n por 1/ x p *y q y obtendremos la siguiente:
que alcanzar� su m�xima magnitud cuando la adquiera la expresi�n inicial.
Representemos as� a la expresi�n obtenida

La suma de todos los factores ser� igual a
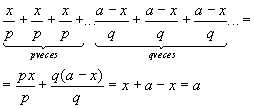
es decir, ser� una magnitud constante.
Si nos basamos en lo demostrado anteriormente deduciremos que el producto

alcanza el m�ximo valor al ser iguales sus factores, es decir, cuando
Sabemos que a � x = y ; sustituyendo el antecedente de la segunda raz�n y alterando el orden de los medios, resultar�
De esta forma, el producto de x p *y q alcanza su m�ximo valor, si la suma x+ y es constante, cuando
Siguiendo semejante razonamiento puede demostrarse que los productos
Volver
5. �Qu� suma ser� la menor?
El lector que desee abordar la demostraci�n de teoremas algebraicos de valor pr�ctico, puede demostrar por s� mismo el siguiente principio:
- La suma de dos n�meros, cuyo producto es constante, alcanza el valor m�nimo cuando dichos n�meros son iguales. Por ejemplo, para el producto 36 : 4 + 9 = 13, 3 + 12 = 15, 2 + 18 = 20, 1 + 36 = 37 y, por �ltimo, 6 + 6 = 12.
- La suma de varios n�meros, cuyo producto es invariable, ser� la menor cuando las magnitudes de los n�meros dados sean id�nticas. Por ejemplo, para 216: 3 + 12 + 6 = 21, 2 + 18 + 6 = 26, 9 + 6 + 4 = 19, mientras que 6 + 6 + 6 = 18.
Volver
6. El tronco de mayor volumen
Problema
De un tronco cil�ndrico debe sacarse una viga rectangular del m�ximo volumen. �Qu� forma ha de tener su secci�n? (fig. 23)

|
| Figura 23 |
Soluci�n
De acuerdo con el teorema de Pit�goras, si los lados de la secci�n rectangular son x e y , tendremos
Donde d es el di�metro del tronco. El volumen de la viga ser� el m�ximo cuando la superficie de su secci�n sea tambi�n la mayor, es decir, cuando xy alcance la mayor magnitud. Mas si xy tiene su m�ximo valor, tambi�n lo alcanzar� x 2 y 2 . Y como la suma x 2 + y 2 es constante, el producto x 2 y 2 ser� el mayor, como demostramos antes, cuando
Por lo tanto, la secci�n de la viga debe ser cuadrada.
Volver
7. Dos parcelas de tierra
Problemas
- �Qu� forma ha de tener una parcela rectangular de un �rea dada, para que la longitud de su cerca sea la menor posible?
- �Qu� forma debe tener una parcela rectangular para que, con una longitud fija de su cercado, tenga aqu�lla la mayor �rea posible?
-
La forma de la parcela rectangular se determina por la relaci�n entre sus
lados,
x
e
y.
El �rea de una parcela cuyos lados sean
x
e
y es igual a
xy,
y la longitud de la cerca 2
x
+ 2
y
. Esta �ltima ser� la menor si
x + y
tiene el menor valor.
Si el producto
xy
es constante, la suma
x
+
y
es la menor si
x = y.
Por lo tanto, el rect�ngulo que buscamos debe ser un cuadrado.
- Si x e y son los lados de una parcela rectangular, la longitud de su cerca ser� 2 x + 2 y , y su �rea, xy . Este producto es el mayor cuando lo es tambi�n el producto 4 xy , o sea, 2 x *2 y ; este �ltimo alcanza su m�ximo valor (si la suma de sus factores 2 x + 2 y es constante) cuando 2 x = 2 y , es decir, si la parcela es un cuadrado.
Volver
8. La cometa
Problema
B�squese la forma de una cometa con un sector circular que tenga la mayor superficie, partiendo de un per�metro previamente dado.
Soluci�n
Precisadas las condiciones del problema, debemos hallar la relaci�n entre la longitud del arco del sector y su radio que nos de la mayor superficie posible, sin alterar el per�metro dado.
Si el radio de un sector es x y el arco y , el per�metro 1 y la superficie S , se expresar�n as� (fig. 24).

|
| Figura 24 |
S = xy/ 2 = x(I - 2 x) /2
La magnitud de S llega a su m�ximo valor, con los valores de x que lo proporcionen tambi�n a la expresi�n 2 x (1- 2 x), o sea, el cu�druplo de la superficie, Y como la suma 2 x+ (1- 2 x) = l es una magnitud constante, su producto ser� el mayor cuando 2x= l -2x, de donde
y = l � 2 * l /4 = l /2
De esta forma, un sector con per�metro dado tiene la mayor superficie cuando su radio representa la mitad del arco (es decir, la longitud de su arco es igual a la suma de los radios; o la longitud de la l�nea curva de su per�metro es igual a la longitud de la quebrada). El �ngulo del sector es aproximadamente de 115�, o sea, dos radianes. Las cualidades de vuelo de tal cometa ya es una cuesti�n ajena a este problema.
Volver
9. La construcci�n de una casa
Problema
En el solar de una casa derruida, donde queda en pie tan s�lo una pared de 12 m de largo, se proyecta la construcci�n de un nuevo edificio aprovechando el muro existente. La superficie de la nueva casa debe ser de 112 m 2 . Las condiciones econ�micas para la obra son:
- La reparaci�n de un metro lineal de pared vieja equivale al 25% de lo que cuesta levantar una nueva.
- El derribo de un metro lineal de la pared vieja y la construcci�n de una nueva con ladrillo recobrado alcanza el 50% de lo que costar�a levantarla con material de f�brica.
Soluci�n
Supongamos que se conservan x metros de pared y los dem�s 12- x se derriban para, con el material recuperado, levantar una parte de la pared de la futura casa (fig. 25).

|
| Figura 25 |
Si el valor de cada metro lineal levantado con ladrillo nuevo es igual a a, la reparaci�n de x metros de pared vieja costar� ax /4 ; la edificaci�n de los 12- x metros de pared costar� a (12-x)/ 2; el resto de la pared, a [ y - (12 - x )], es decir, a ( y+x-12 ); la tercera parte de la pared, ax , y la cuarta, ay . Todo el trabajo equivaldr� a
La �ltima expresi�n llegar� a su m�nima magnitud cuando la suma 7 x + 8 y alcance su valor m�nimo.
Sabemos que el �rea de esta casa xy es igual a 112; por lo tanto,
Si el producto es constante, la suma 7 x * 8 y tomar� el menor valor cuando
de donde
Sustituyendo el valor de y en la ecuaci�n xy = 112
tendremos:
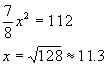
Y siendo la longitud de la antigua pared de 12 m debe desmontarse tan s�lo 0,7 m de dicha pared.
Volver
10. La parcela
Problema
Con el fin de construir una casa de campo se precisaba cercar la pared destinada a este fin. Cont�base con material para l metros lineales de valla. Adem�s, en uno de los lados de la parcela pod�a emplearse una cerca construida con anterioridad.
En estas condiciones, �c�mo hubo que cercar la parcela rectangular para abarcar la mayor superficie posible?
Soluci�n
Supongamos que la longitud de la parcela (seg�n la cerca) es igual a x, y el ancho (es decir, la dimensi�n de la parcela en la direcci�n perpendicular a la cerca) equivale a y (fig. 26).
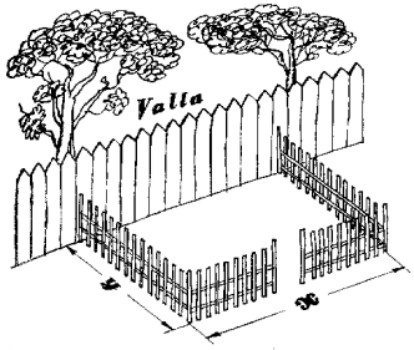
|
| Figura 26 |
En este caso, para cercar esta parcela fueron precisos x +2 y metros de cerca, de forma que
El �rea de la parcela ser�
que alcanzar� un valor m�ximo simult�neamente con el valor 2 y ( l - 2 y ) (duplo del �rea), producto de dos factores, siendo l constante. Por eso, para conseguir la mayor �rea de la parcela, debe tener lugar la siguiente igualdad
de donde
En otras palabras: x = 2 y , es decir, la longitud de la parcela debe ser el doble de la anchura.
Volver
11. El canal�n de secci�n m�xima
Problema
Hemos de doblar en forma de canal�n una hoja rectangular de chapa (fig. 27).

|
| Figura 27 |

|
| Figura 28. |
�Cu�l ha de ser la anchura de los costados y qu� �ngulo deben formar para que la secci�n del canal�n tenga la m�xima superficie? (fig. 29).

|
| Figura 29. |
Soluci�n
Representemos por l la anchura de la hoja; por x, la de los costados doblados, y por y la del fondo del canal�n. Introduzcamos una medida m�s, la inc�gnita z , cuyo valor aparece con toda claridad en la fig. 30.

|
| Figura 30. |
La superficie del trapecio que representa la secci�n del canal�n ser�
La tarea consiste en determinar cu�les han de ser los valores de x, y, z para que S alcance la mayor magnitud admitiendo que la suma 2 x + y (anchura de la hoja) es una constante l. Pasemos a las transformaciones:
S 2 alcanzar� su m�xima magnitud con los valores de x, y y z que la proporcionen tambi�n a 3S2.
3 S 2 puede presentarse en forma de producto
La suma de estos factores ser�:
es decir, es invariable. Por eso, el producto de nuestros cuatro factores llega al m�ximo cuando �stos son iguales entre s�, es decir
x + z = 3 x - 3 z.
Por la primera ecuaci�n sabemos que
y como
entonces
De la segunda ecuaci�n, resulta
Como el cateto z es igual a la mitad de la hipotenusa x (fig. 30), el �ngulo opuesto a este cateto ser� igual a 30�, y el �ngulo de inclinaci�n de los costados equivaldr� a 90� + 30� = 120�.
En fin, el canal�n alcanzar� la mayor secci�n cuando sus dobleces tengan la forma de 3 lados contiguos de un hex�gono regular.
Volver
12. El embudo de mayor capacidad
Problema
Debemos construir la parte c�nica de un embudo vali�ndonos de un c�rculo de hojalata. Para ello se corta un sector en dicho c�rculo y, con el resto, se construye el cono (fig. 31).

|
| Figura 31 |
�Cu�ntos grados debe tener el arco del sector que se ha cortado para que el embudo alcance la mayor capacidad posible?
Soluci�n
La longitud del arco de aquella parte que se aprovecha para el cono se representa con la x (en unidades lineales). Por lo tanto, la generatriz ser� el radio, R , del c�rculo de hojalata, y la circunferencia de la base ser� igual a x. El radio r , de la base del cono, se determinar� en la igualdad
de donde
La altura del cono, seg�n el teorema de Pit�goras, ser� (fig. 31).
El volumen de este cono equivaldr� a
Y esta expresi�n alcanza su mayor valor simult�neamente con la expresi�n

y con su cuadrado
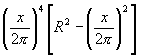
y como
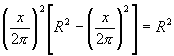
es un valor constante, el �ltimo producto (como se demuestra en las p�ginas anteriores) llega a su m�ximo valor cuando x tiene una magnitud tal, que
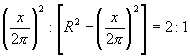
de donde
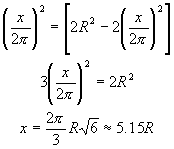
El arco x tiene alrededor de 295� y, en consecuencia, el arco del sector cortado equivaldr� aproximadamente a 65 grados.
Volver
13. La iluminaci�n m�s intensa
Problema
�A qu� altura de la mesa debe hallarse la llama de una vela para que ilumine con la mayor intensidad a una moneda colocada sobre dicha mesa?
Soluci�n
Puede parecer que para conseguir el objetivo propuesto deba colocarse la llama lo m�s baja posible. Esto es falso. En esas condiciones, los rayos de luz caen muy oblicuos. Mas si se eleva la vela para que los rayos caigan m�s verticales, el foco de luz se aleja. Por eso, la iluminaci�n m�s ventajosa es, sin duda, la que se realiza desde una altura media.

|
| Figura 32 |
Denominemos a esta altura con la letra x (fig. 32). La distancia BC, que media entre la moneda B y la base C de la perpendicular que pasa por la llama A, la designaremos con la letra a . Si la claridad de la llama es i , de acuerdo con las leyes de la �ptica, la luminosidad ser� expresada as�:
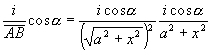
donde a es el �ngulo de ca�da de los rayos AB. Y como
a luminosidad ser�

Esta expresi�n alcanza su m�ximo valor cuando sin variar la x, adquiera tambi�n su mayor magnitud el cuadrado de aqu�lla
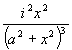
Omitamos el valor del factor i 2 por su magnitud constante y transformemos el resto de la expresi�n analizada como sigue:

La expresi�n transformada alcanza su mayor magnitud cuando la alcanza la expresi�n

por cuanto el factor constante introducido, a 4 , no influye en el valor de x con el cual el producto llega a su m�s elevada magnitud.
Partiendo de que la suma de las primeras potencias de estos factores

es una magnitud constante, se deduce que el producto examinado alcanza su m�s alto valor cuando
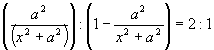
Tenemos una ecuaci�n:
que al resolverla resultar�
La moneda es iluminada con la mayor intensidad cuando el foco de luz se encuentra a una altura de 0,71 de la distancia desde la proyecci�n del foco hasta la moneda. El conocimiento de esta correlaci�n ayuda a instalar con la mayor acierto el alumbrado en los lugares de trabajo.
Volver
|
|
|
|