Prefacio
Del prefacio del autor a la tercera edici�n rusa
1. La quinta operaci�n matem�tica
2. El idioma del �lgebra
3. En ayuda de la aritm�tica
4. Las ecuaciones de Diofanto
5. La sexta operaci�n matem�tica
6. Ecuaciones de segundo grado
7. La magnitud mayor y la menor
8. Progresiones
9. La s�ptima operaci�n matem�tica
Bajar Documento Completo

Capitulo Sexto
ECUACIONES DE SEGUNDO GRADO
Contenido
1. El apretón de manos
2. El enjambre de abejas
3. La manada de monos
4. Previsión de las ecuaciones
5. El problema de Euler
6. Los altavoces
7. El álgebra del vuelo a la Luna
8. "Ejercicio complicado"
9. �Qué números son?
1. El apretón de manos
Problema
Las personas que asistieron a una reunión se estrecharon la mano. Uno de ellos advirtió que los apretones de mano fueron 66. �Cuántas personas concurrieron a la reunión?
Solución
La cuestión se resuelve con facilidad si recurrimos al álgebra. Cada una de las x personas dio la mano a las otras x- 1. Por tanto, el total de apretones de manos debe ser x (x - l). Además hay que tener en cuenta que cuando Ivanov da la mano a Petrov, Petrov estrecha la mano de Ivanov; estos dos apretones de manos deben ser considerados como uno solo. Por eso, el número de apretones de manos contados es dos veces menor que x ( x -1). En consecuencia surge la ecuaci&oacuute;n
o sea, que después de las correspondientes transformaciones se tendrá
de donde
como quiera que la raíz negativa (-11 personas) carece de todo sentido, la rechazamos, conservando únicamente la primera: en la reunión estuvieron 12 personas.
Volver
2. El enjambre de abejas
Problema
En la antigüedad estaba muy extendida en la India una diversión singular: la solución de rompecabezas en competiciones públicas. Los manuales de matemáticas de ese país contribuían a la celebración de tales campeonatos de cálculo mental. "Aplicando las reglas aquí expuestas -escribía el autor de uno de dichos libros -, un hombre inteligente puede idear miles de problemas semejantes. Así como el Sol hace palidecer las estrellas con sus destellos, un hombre discreto eclipsa la gloria de otro hombre en los concursos populares, proponiendo y resolviendo problemas algebraicos". En el original, estas palabras presentan un aspecto más poético, por cuanto el libro está escrito en verso. Los problemas también aparecen versificados. Enunciemos en prosa uno de estos rompecabezas.
Un grupo de abejas, cuyo número era igual a la raíz cuadrada de la mitad de todo su enjambre, se posó sobre un jazmín, habiendo dejado muy atrás a 8/9 del enjambre; sólo una abeja del mismo enjambre revoloteaba en torno a un loto, atraída por el zumbido de una de sus amigas que cayó imprudentemente en la trampa de la florecilla, de dulce fragancia.
�Cuántas abejas formaban el enjambre?
Solución
Si expresamos el número buscado de abejas del enjambre con la letra x , tendremos la ecuación
Puede simplificarse la ecuación introduciendo una incógnita auxiliar:
Entonces x = 2 y 2 , por lo que resultará la siguiente ecuación:
La ecuación tiene dos raíces para y:
y otras dos para x
Mas, como el número de abejas debe ser entero y positivo, es válida sólo la primera raíz: el enjambre constaba, pues, de 72 abejas. Comprobémoslo:
Volver
3. La manada de monos
Problema
Otro de los problemas indios puede ser presentado en verso tal y como fue traducido por Lébedev, autor del excelente libro �Quién inventó el álgebra?
|
Regocíjanse los monos
divididos en dos bandos:
su octava parte al cuadrado
en el bosque se solaza.
Con alegres gritos, doce atronando el campo están. �Sabes cuántos monos hay en la manada, en total? |
Solución
Si el número total de la manada es x, entonces:
de donde

|
| Figura 15 |
El problema tiene dos soluciones positivas: en la manada puede haber 48 y 16 monos. Las dos soluciones satisfacen por las condiciones del problema.
Volver
4. Previsión de las ecuaciones
En los casos examinados y en dependencia de las condiciones del problema, hemos hecho diferente uso de las dos raíces obtenidas. En el primer caso hemos desechado la raíz negativa por no responder al contenido del problema; en el segundo, hemos renunciado a la raíz fraccionaria y negativa y, en el tercero, por el contrario, hemos aceptado las dos raíces. La presencia de una segunda solución es, a veces, completamente inesperada no sólo para quien resuelve el problema, sino también para su autor; pongamos un ejemplo de cómo la ecuación resulta más previsora que el mismo que la establece.
Problema
Una pelota ha sido lanzada al aire a una velocidad de 25 m por segundo. �Al cabo de cuántos segundos se encontrará la pelota a 20 m de altura?
Solución
Para los cuerpos lanzados al alto, y libres en su ascensión de toda resistencia, la mecánica establece las siguientes proporciones entre la altura a la que sube el cuerpo sobre la tierra ( h ), su. velocidad inicial ( v ), el aceleramiento de la fuerza de gravedad ( g ) y el tiempo ( t ):
En este ejemplo concreto podemos hacer caso omiso de la resistencia aérea, por cuanto es muy pequeña cuando la velocidad no es de consideración. A fin de simplificar la operación, demos a g, el valor 10 m, en lugar de 9,8 m (el error es tan sólo del 2%). Sustituyendo h, v, g por sus valores en la fórmula indicada, tendremos la siguiente ecuación:
y después de quitar denominadores y simplificar
Resultan las raíces:
La pelota estará dos veces a la altura de 20 m: al primer segundo y después de cuatro segundos de haber sido lanzada.
Acaso parezca inverosímil y, al no reflexionar, puede rechazarse el segundo resultado. Sin embargo, esto sería erróneo. El segundo resultado es completamente lógico: la pelota puede encontrarse dos veces a la altura de 20 m: una, al ascender, y otra, al descender.
Se deduce con facilidad que la pelota puede ascender durante 2,5 segundos con la velocidad inicial de 25 m, llegando a una altura de 31,25 m. Después de alcanzar la altura de 20 m, (al segundo de ascenso) la pelota seguirá elevándose durante 1,5 segundos más, al cabo de lo cual descenderá durante 1,5 segundos hasta la altura de 20 m, llegando al suelo un segundo después.
Volver
5. El problema de Euler
Problema
Al referirse Stendhal en su Autobiografía a sus años de estudiante, escribe lo siguiente:
"En su casa (la de su maestro de matemáticas) encontré a Euler con su problema acerca de los huevos que la campesina llevaba al mercado... Esto fue para mí un descubrimiento. Comprendí lo que significaba valerse de un arma como el álgebra. Pero �demonios!, nadie me lo había explicado antes..."
He aquí el problema de la Introducción al álgebra, de Euler que tan fuerte impresión produjera en Stendhal.
Dos campesinas llevaron en total 100 huevos al mercado. Una de ellas tenía más mercancía que la otra, pero recibió por ella la misma cantidad de dinero que la otra. Una vez vendidos todos, la primera campesina dijo a la segunda: "si yo hubiera llevado la misma cantidad de huevos que tú, habría recibido 15 cruceros". La segundo contestó: "Y si yo hubiera vendido los huevos que tenías tú habría sacado de ellos 6 2 / 3 , cruceros". �Cuántos huevos llevó cada una?
Solución
Supongamos que la primera campesina tenía x huevos. La segunda tendría 100 - x. Si la primera hubiera tenido 100 - x habría sacado de ellos 15 cruceros. Eso quiere decir que la primera campesina vendió los huevos
cada uno
De esta manera vemos que la segunda campesina vendió los huevos a
cada uno.
Hallemos ahora la cantidad obtenida por cada campesina: la primera:
la segunda
Y como ambas recibieron lo mismo, entonces
que después de las correspondientes transformaciones resultará
x 2 + 160x � 8000 = 0,
de donde
x 1 = 40, x 2 = 200.
La raíz negativa carece de sentido en el presente caso. El problema no tiene más que un resultado: la primera campesina llevó al mercado 40 huevos y la segunda 60.
El problema puede resolverse con más brevedad. El procedimiento es más ingenioso, aunque más difícil.
Supongamos que la segunda campesina llevó al mercado k huevos más que la primera. Ambas recibieron por su mercancía la misma suma de dinero.
Esto significa que la primera vendió los huevos k veces más caros que la segunda. Si hubieran cambiado la mercancía, la primera campesina hubiera tenido k veces más huevos que la segunda y los habría vendido k' veces más caros, recibiendo k 2 más dinero que aquélla. Por lo tanto tendremos:
de donde resulta que
Ahora no nos queda más que dividir los 100 huevos proporcionalmente a 3 y a 2. La primera campesina llevó 40 huevos y la segunda, 60.
Volver
6. Los altavoces
Problema
En la plaza hay instalados 5 altavoces distribuidos en dos grupos: uno de ellos consta de 2 aparatos, y el otro, de 3. La distancia que separa los dos grupos es de 50 m. �Dónde habrá que colocarse para que el sonido de ambos grupos se oiga con la misma intensidad?
Solución
Si designamos con x la distancia que separa el punto buscado del grupo de dos altavoces, entonces, la distancia entre este punto y el otro grupo será 50 - x (véase la fig. 16).

|
| Figura 16 |
Puesto que la intensidad del sonido disminuye en proporción al cuadrado de la distancia, tendremos la siguiente ecuación:
que después de efectuar las operaciones, aparece como sigue:
La ecuación tiene dos raíces:
x 1 = 22,5,
x 2 = - 222,5.
La raíz positiva corresponde a la pregunta formulada en el problema: el punto citado se encuentra a 22,5 m de distancia del grupo de dos altavoces, y, en consecuencia, a 27,5 m del grupo de tres.
Pero �qué significa la raíz negativa? �Tiene algún sentido?
Indudablemente. El signo menos significa que el segundo punto de idéntica audición se encuentra en dirección o p u e s t a al punto positivo que se tomó al establecer la ecuación.
Partiendo del lugar ocupado por los dos reproductores y en la dirección conveniente llegamos a los 222,5 m, punto en el que el sonido de ambos grupos de altavoces se oye con la misma intensidad. Este punto dista
del grupo de tres aparatos.
Así pues se han encontrado dos puntos de igual audición colocados en la línea formada por las fuentes de sonido. En esta línea no hay más puntos donde coincida la intensidad de sonidos, pero fuera de ella, sí. Puede demostrarse que el lugar geométrico de los puntos que responden a las condiciones del problema es la circunferencia que pasa por los dos puntos hallados, cual si fueran los extremos de su diámetro. Esta circunferencia, como vernos, limita un espacio bastante extenso (la parte rayada en la figura) dentro del cual la intensidad auditiva del grupo formado por dos altavoces supera la audición del grupo de tres aparatos; fuera del espacio indicado se observa el fenómeno opuesto.
Volver
7. El álgebra del vuelo a la Luna
Del mismo modo como se han encontrado los puntos de igual audición de dos tipos de altavoces, se puede encontrar también puntos de igual atracción del cohete cósmico por dos cuerpos celestes, la Tierra y la Luna. Busquemos estos puntos.
De acuerdo con la ley de Newton, la fuerza de atracción recíproca de dos cuerpos es directamente proporcional al producto de las masas que se atraen, e inversamente proporcional al cuadrado de la distancia entre ellos. Si designamos con M la masa de la Tierra y con x la distancia entre ella y el cohete, la fuerza con que la Tierra atrae cada gramo de masa de la nave aérea se expresará mediante
donde k es la fuerza de atracción recíproca de un gramo por un gramo a la distancia de 1 cm.
La fuerza con que la Luna atrae cada gramo del cohete en ese mismo punto
será:
donde m es la masa de la Luna y 1 la distancia que la separa de la Tierra (se presupone que el cohete se halla en la recta que une los centros de la Tierra y de la Luna). El problema exige que
es decir
La relación M/m , según la Astronomía, equivale aproximadamente a 81,5. m
Aplicándola tendremos
por lo cual
Al despejar la incógnita x resulta:
x 1 = 0,9 l , x 2 = 1, 12 l .
Al igual que en el problema de los altavoces, se llega a la conclusión de que en la línea que une la Tierra y la Luna existen dos puntos buscados donde la atracción de ambos planetas actúa sobre el cohete con idéntica intensidad: uno a 0,9 de la distancia que separa los planetas partiendo del centro de la Tierra; el otro, a 1,12 de esta misma distancia. Como quiera que la distancia 1 entre los centros de la Tierra y la Luna » 384 000 km, uno de los puntos buscados se encuentra a 346.000 km de la Tierra; el otro, a 430.000 km. Sabemos ya por el problema anterior que esa misma propiedad caracteriza a todos los puntos de la circunferencia que pasa por los dos puntos hallados, tomados como los dos extremos del diámetro. Si hacemos girar esa circunferencia tomando como eje la línea que une los centros de la Tierra y la Luna describirá una esfera cuyos puntos responden a las exigencias del problema.
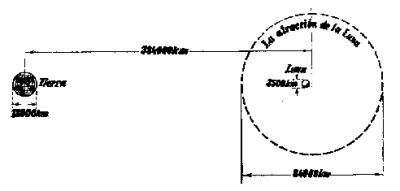
|
| Figura 17 |
El diámetro de esa esfera llamada "esfera de atracción" de la Luna (fig. 17) será igual a:
Mucha gente piensa erróneamente que para acertar con un cohete en la Luna es bastante hacerle alcanzar la esfera de atracción de ésta.
A primera vista parece que si el cohete se halla dentro de la esfera de atracción (y su velocidad no es muy grande) él debe caer forzosamente en la superficie de la Luna, por cuanto la fuerza de atracción de la Luna "supera" a la de la Tierra.
Si fuera así entonces la tarea del vuelo a la Luna sería mucho más fácil, pues no haría falta acertar a la Luna cuyo diámetro se ve en el cielo bajo un ángulo de 1/2', sino a un globo de 84 000 km de diámetro, la dimensión del cual equivale a 12'.
Pero no es difícil demostrar el error de razones parecidas. Supongamos que un cohete lanzado desde la Tierra hacia la Luna, perdiendo su velocidad por causa de la atracción terrestre, llegue a la esfera de la atracción lunar teniendo la velocidad cero. �Va a caer éste en la Luna? �De ningún modo!
En primer lugar, dentro de la esfera de atracción lunar hay también la atracción terrestre. Por eso al lado de la línea de Tierra - Luna la fuerza de atracción de la Luna no va sólo a "superar" a la terrestre, sino éstas se sumarán de acuerdo con la regla del paralelogramo de fuerzas y obtendremos una fuerza resultante no dirigida directamente a la Luna (sólo en la línea de Tierra - Luna esta fuerza resultante sería dirigida directamente al centro de la Luna).
En segundo lugar (y esto es lo principal), la misma Luna no es un blanco inmóvil y si nosotros queremos saber cómo va a moverse con relación a ésta el cohete (si va a "caer" en ella), hace falta tener en cuenta la velocidad del cohete respecto a la Luna. Mas esta velocidad no equivale a cero, pues la misma Luna se mueve alrededor de la Tierra con una velocidad de 1 km/seg. Por eso la velocidad del movimiento del cohete con relación a la Luna es demasiado grande para que ésta pueda atraer el cohete o por lo menos detenerlo en la esfera de su atracción como un satélite artificial. En realidad la atracción de la Luna empieza a ejercer influencia considerable en el movimiento del cohete antes de acercarse éste a la esfera de atracción de la Luna. En la balística celeste hay que tener en cuenta la atracción de la Luna desde el momento cuando el cohete llegue a la esfera de influencia de la Luna que tiene el radio de 66 000 km. En este caso ya se puede considerar el movimiento del cohete con relación a la Luna al olvidar por completo la atracción terrestre, pero hace falta tener en consideración la velocidad exacta (respecto a la Luna) con que el cohete entra en la esfera de influencia de la Luna. Por eso es natural que el cohete debe ser lanzado a la Luna por una trayectoria que puede asegurar que la velocidad (con relación a la Luna) de entrada en la esfera de influencia de la Luna esté dirigida directamente a la Luna. Para eso la esfera de influencia de la Luna debe chocar con el cohete que se mueve a su encuentro. Como se ve no es una cosa tan fácil acertar a la Luna como a un globo de 84 000 km de diámetro.
Volver
8. "Ejercicio complicado"
Problema
Son muchos los que conocen el cuadro Ejercicio complicado, (año 1895) de Bogdánov - Belski, pero muy pocos se percatan del contenido del ,,ejercicio complicado" al contemplar dicho cuadro.

|
| Figura 18 |
Trátase de resolver rápida y mentalmente el siguiente ejercicio:
El ejercicio, efectivamente, no es fácil. Sin embargo, los alumnos del cuadro lo resuelven con facilidad. En la figura del maestro, el pintor reprodujo a S. Rachinski, profesor de Ciencias Naturales, que abandonó la cátedra de la universidad para convertirse en un sencillo maestro rural. El inteligente pedagogo cultivaba en su escuela el cálculo mental, basado en el hábil empleo de las propiedades de los números. Los números 10, 11, 12, 13 y 14 tienen una curiosa propiedad:
10 2 + 11 2 + 12 2 = 13 2 + 14 2
Comoquiera que
es fácil hallar mentalmente que la expresión reproducida en el cuadro es igual a 2.
El álgebra nos ofrece los medios necesarios para plantear con más amplitud la cuestión de esta interesante particularidad de las series de números. �Es acaso ésta la única serie de cinco números consecutivos, en la que la suma de los cuadrados de los tres primeros es igual a la suma de los cuadrados de los otros dos?
Solución
Si expresamos el primero de los números buscados con x , tendremos la siguiente ecuación:
x 2 +(x + 1) 2 + (x + 2) 2 = (x + 3) 2 + (x+ 4 ) 2
Sin embargo, es más cómodo expresar con x, no el primer número de los buscados, sino el segundo. Entonces la ecuación tendrá un aspecto más sencillo:
(x �
Al abrir los paréntesis y reducir los términos semejantes, resultará:
de donde
Existen por consiguiente, dos series de números que tienen las propiedades exigidas: la serie de Rachinski
y la serie
Así es, en efecto,
Volver
9. �Qué números son?
Problema
Hállense tres números consecutivos en los que el cuadrado del número del medio sea mayor en una unidad al producto de los dos restantes.
Solución
Si la primera cifra es x, tendremos la ecuación:
Abriendo los paréntesis resultará la siguiente ecuación:
de la cual no puede deducirse la magnitud de x . Esto muestra que la igualdad formulada por nosotros es una identidad; y la identidad es efectiva, no sólo cuando sus letras encierran un valor determinado, como ocurre en la ecuación, sino para cualquier valor de las mismas. Por ello, tres números consecutivos, sean los que fueren, poseen dicha propiedad. En efecto, tomemos tres cifras al azar:
y nos convenceremos de que
Lo inevitable de esta correlación salta más a la vista si expresamos la segunda cifra con la letra x , con lo que
Es decir, se trata de una identidad evidente.
Volver
|
|
|
|