Prefacio
Del prefacio del autor a la tercera edici�n rusa
1. La quinta operaci�n matem�tica
2. El idioma del �lgebra
3. En ayuda de la aritm�tica
4. Las ecuaciones de Diofanto
5. La sexta operaci�n matem�tica
6. Ecuaciones de segundo grado
7. La magnitud mayor y la menor
8. Progresiones
9. La s�ptima operaci�n matem�tica
Bajar Documento Completo

Contenido
1. El arte de plantear ecuaciones
2. La vida de Diofanto
3. El caballo y el mulo
4. Los cuatro hermanos
5. Las aves de la orilla
6. El paseo
7. El artel de segadores
8. Las vacas en el prado
9. El problema de Newton
10. El cambio de las manecillas del reloj
11. Coincidencia de las saetas
12. El arte de adivinar n�meros
13. Un supuesto absurdo
14. La ecuaci�n piensa por nosotros
15. Curiosidades y sorpresas
16. En la peluquer�a
17. El tranv�a y el peat�n
18. El barco y la balsa
19. Dos botes de caf�
20. Velada
21. Exploraci�n marina
22. En el vel�dromo
23. Carrera de motocicletas
24. Velocidad media
25. M�quinas de c�lculo r�pido
1. El arte de plantear ecuaciones.
El idioma del �lgebra es la ecuaci�n. "Para resolver un problema referente a n�meros o relaciones abstractas de cantidades, basta con traducir dicho problema, del ingl�s u otra lengua al idioma algebraico�, escribi� el gran Newton en su manual de �lgebra titulado Aritm�tica Universal. Isaac Newton mostr� con ejemplos c�mo deb�a efectuarse la traducci�n. He aqu� uno de ellos:
| En la lengua vern�cula: | En el idioma del �lgebra: |
| Un comerciante ten�a una determinada suma de dinero | x |
| El primer año se gast� 100 libras | x - 100 |
|
Aument� el resto con un tercio de �ste |
|
| Al año siguiente volvi� a gastar 100 libras |
|
| y aument� la suma restante en un tercio de ella |
|
| El tercer año gast� de nuevo 100 libras |
|
|
Despu�s de que hubo agregado su tercera parte |
|
| el capital lleg� al doble del inicial |
|
Soluci�n
Para determinar cu�l es el capital inicial del comerciante no queda m�s que resolver la �ltima ecuaci�n.
La soluci�n de una ecuaci�n es, con frecuencia, tarea f�cil; en cambio, plantear la ecuaci�n a base de los datos de un problema suele ser m�s dif�cil. Hemos visto que el arte de plantear ecuaciones consiste, efectivamente, en traducir "la lengua vern�culo a la algebraica". Pero el idioma del �lgebra es lac�nico en extremo, por eso no todos los giros del idioma materno son de f�cil traducci�n. Las traducciones pueden ser muy distintas por el grado de su dificultad, como puede convencerse el lector a la vista de los ejemplos de ecuaci�n de primer grado expuestos.
Volver
2. La vida de Diofanto
Problema
La historia ha conservado pocos rasgos biogr�ficos de Diofanto, notable matem�tico de la antigüedad. Todo lo que se conoce acerca de �l ha sido tomado de la dedicatoria que figura en su sepulcro, inscripci�n compuesta en forma de ejercicio matem�tico. Reproducimos esta inscripci�n:
| En la lengua vern�cula | En el idioma del �lgebra: |
| �Caminante! Aqu� fueron sepultados los restos de Diofanto. Y los n�meros pueden mostrar, �oh, milagro!, cu�n larga fue su vida, | x |
| cuya sexta parte constituy� su hermosa infancia. | x / 6 |
| Hab�a transcurrido adem�s una duod�cima parte de su vida, cuando de vello cubri�se su barbilla | x / 12 |
| Y la s�ptima parte de su existencia transcurri� en un matrimonio est�ril. | x / 7 |
| Pas� un quinquenio m�s y le hizo dichoso el nacimiento de su precioso primog�nito, | 5 |
| que entreg� su cuerpo, su hermosa existencia, a la tierra, que dur� tan s�lo la mitad de la de su padre | x / 2 |
| Y con profunda pena descendi� a la sepultura, habiendo sobrevivido cuatro años al deceso de su hijo |
|
| Dime cu�ntos años hab�a vivido Diofanto cuando le lleg� la muerte. | |
Soluci�n
Al resolver la ecuaci�n y hallar el valor de la inc�gnita, 84, conocemos los siguientes datos biogr�ficos de Diofanto: se cas� a los 21 años, fue padre a los 38, perdi� a su hijo a los 80 y muri� a los 84.
Volver
3. El caballo y el mulo
Problema
He aqu� un antiguo ejercicio muy sencillo y f�cil de traducir al idioma de] �lgebra.
"Un caballo y un mulo caminaban juntos llevando sobre sus lomos pesados sacos. Lament�base el jamelgo de su enojosa carga, a lo que el mulo le dijo: "�De qu� te quejas? Si yo te tomara un saco, mi carga ser�a el doble que la tuya. En cambio, si te doy un saco, tu carga se igualar� a la m�a". �Decidme, doctos matem�ticos, cu�ntos sacos llevaba el caballo, y cu�ntos el mulo?".
Soluci�n
| Si yo te tomara un saco | x - 1 |
| mi carga | y + 1 |
| ser�a el doble que la tuya. | y + 1 = 2 (x - 1) |
| Y si te doy un saco, | y - 1 |
| tu carga | x + 1 |
| se igualar� a la m�a | y - 1 = x + 1 |
Hemos planteado el problema mediante un sistema de ecuaciones con dos inc�gnitas:
�
y � x = 2
Una vez resuelto el sistema vemos que x = 5, y = 7.
El caballo llevaba 5 sacos, y el mulo, 7.
Volver
4. Los cuatro hermanos
Problema
Cuatro hermanos tienen 45 rublos. Si el dinero del primero es aumentado en 2 rublos, el del segundo reducido en 2 rublos, se duplica el del tercero y el del cuarto se reduce a la mitad, todos los hermanos tendr�n la misma cantidad de rublos. �Cu�nto dinero ten�a cada uno?
Soluci�n
| Los cuatro hermanos tienen 45 rublos | x + y + z + t = 45 |
| Si al dinero del primero se le agregan 2 rublos | x + 2 |
| al del segundo se restan 2 rublos | y - 2 |
| el del tercero se duplica, | 2z |
| y el del cuarto se divide por dos | t / 2 |
| a todos los hermanos les quedar� la misma cantidad de rublos | x + 2 = y - 2 = 2z = t / 2 |
La �ltima ecuaci�n nos permite plantear tres ecuaciones independientes:
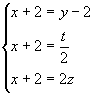
de donde
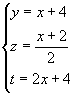
Colocando estos valores en la primera ecuaci�n, tendremos:
de donde x = 8.
A continuaci�n hallamos que y = 12, z = 5, t = 20. Por lo tanto, los hermanos ten�an: 8, 12, 5 y 20 rublos.
Volver
5. Las aves de la orilla
Problema
En las obras de un matem�tico �rabe del siglo XI hallamos el siguiente problema:
A ambas orillas de un r�o crecen dos palmeras, la una frente a la otra. La altura de una es de 30 codos, y la de la otra, de 20. La distancia entre sus troncos, 50 codos. En la copa de cada palmera hay un p�jaro. De s�bito los dos p�jaros descubren un pez que aparece en la superficie del agua, entre las dos palmeras. Los p�jaros se lanzaron y alcanzaron el pez al mismo tiempo. �A qu� distancia del tronco de la palmera mayor apareci� el pez?

|
| Figura 5 |
Soluci�n
Mediante la fig. 5 y aplicando el teorema de Pit�goras, establecemos:
Pero AB = AC, por cuanto los p�jaros cubren esta distancia en un mismo tiempo. Por eso,
Al quitar los par�ntesis simplificando la f�rmula nos encontramos con una ecuaci�n de primer grado:
El pez apareci� a 20 codos de la palmera que ten�a 30 codos de altura.
Volver
6. El paseo
Problema
- Pase usted mañana por mi casa - dijo el viejo doctor a un conocido. - Muy agradecido. Saldr� mañana a laas tres. Quiz� desee usted dar tambi�n un paseo. En este caso salga a la misma hora y nos encontraremos a la mitad del camino. - Usted olvida que soy ya viejo y ando tan s�lo tres kil�metros por hora, en tanto que usted, jovenzuelo, cuando m�s despacio va, hace 4 kil�metros por hora. No ser�a ning�n delito que me concediera alguna ventaja. - Tiene raz�n - contest� el joven - . Comoqquiera que yo recorro un kil�metro a la hora m�s que usted, le doy este kil�metro de ventaja, es decir, saldr� de casa un cuarto de hora antes �le ser� suficiente? - Es usted muy amable - aprob� al instante el anciano. El joven cumpli� lo prometido y sali� de su casa a las tres menos cuarto, marchando a 4 kil�metros por hora. El doctor sali� a la calle a las tres en punto y anduvo a tres kil�metros por hora. Cuando se encontraron, el anciano dio la vuelta, yendo juntos a su domicilio. Tan s�lo cuando el joven regres� a su casa comprendi� que debido a la ventaja concedida tuvo que caminar, no el doble, sino el cu�druplo de lo que anduvo el doctor. �A qu� distancia de la casa del doctor estaba la de su joven conocido?
Soluci�n
Expresemos la distancia que separa las casas con la x (km). El joven anduvo en total 2 x , y el doctor, la cuarta parte, es decir x / 2 . Desde que sali� de casa hasta que se encontraron, el doctor recorri� la mitad de cuanto anduvo en total, es decir, x / 4 , y el joven hizo el resto, es decir, 3 x / 4. El anciano camin� x / 12 y el joven 3 x / 16 horas; adem�s, sabemos que �ste camin� � de hora m�s que el doctor. Establezcamos la siguiente ecuaci�n
de donde x = 2,4 km.
Entre las dos casas mediaba una distancia de 2,4 km.
Volver
7. El artel de segadores
En los recuerdos acerca de L. Tolst�i, el conocido f�sico A. Ts�nguer refiere el siguiente problema que agradaba en extremo al eminente escritor:
Problema
"Un artel de segadores deb�a segar dos prados, uno ten�a doble superficie que otro. Durante medio d�a trabaj� todo el personal del artel en el prado grande; despu�s de la comida, una mitad de la gente qued� en el prado grande; y la otra mitad trabaj� en el pequeño. Durante esa tarde fueron terminados los dos tajos, a excepci�n de un reducido sector del prado pequeño, cuya siega ocup� el d�a siguiente completo a un solo segador. �Con cu�ntos segadores contaba el artel?".
Soluci�n
En este ejercicio, adem�s de la inc�gnita fundamental - n�mero de segadores - que expresamos con la x , es conveniente introducir otra inc�gnita complementaria: la superficie del sector segado por un trabajador en un solo d�a, que expresamos con la y .
Aunque el problema no exige que se halle su valor, contribuye a encontrar la ra�z de la x .
Representemos la superficie del prado grande con x e y . Este prado lo segaron durante medio d�a x trabajadores, que segaron

|
| Figura 6 |
Durante la segunda parte del d�a trabaj� all� la mitad del artel, es decir, x / 2 y segaron
Comoquiera que al final de la jornada hab�a sido segado todo el prado, su �rea ser�:
Expresamos ahora la superficie del prado menor mediante x e y . Durante medio d�a se ocuparon en �l x trabajadores y segaron una superficie de
Agreguemos a esto el sector que qued� sin segar, que es igual a y (superficie segada por un trabajador en una jornada), y hallaremos la superficie del prado menor:
No nos queda m�s que traducir al idioma del �lgebra la frase "el primer prado tiene doble superficie que el segundo", y la ecuaci�n quedar� establecida como sigue:
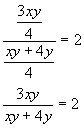
En el artel habla 8 segadores.
Despu�s de haber sido publicada la primera edici�n del Algebra Recreativa, el profesor A. Ts�nguer me envi� una informaci�n detallada y muy interesante, relacionada con este problema. El efecto esencial del problema, a su juicio, reside en que "no es algebraico en absoluto sino aritm�tico, y aunque es muy sencillo se tropieza conciertas dificultades en su resoluci�n debido a que no es de tipo corriente".
"La historia del presente problema es la siguiente - contin�a el profesor A. Ts�nguer - . En la facultad de matem�ticas de la Universidad de Mosc�, cuando estudiaban en ella mi padre e I. Raievski, mi t�o, (amigo �ntimo de L. Tolst�i), entre otras disciplinas se enseñaba algo semejante a la pedagog�a. A este fin, los estudiantes deb�an ir a una escuela p�blica urbana, puesta a disposici�n de la universidad, y en colaboraci�n con expertos y venerables maestros, hac�an pr�cticas pedag�gicas. Entre los compañeros de estudios de Ts�nguer y Raievski hab�a un tal Petrov, que, seg�n cuentan, era persona muy inteligente y original en extremo. Este Petrov (fallecido en su juventud, creo que de tisis) afirmaba que en las clases de aritm�tica embrutec�an a los escolares con problemas y m�todos estereotipados. Para poner de evidencia su punto de vista, Petrov ingeniaba problemas que por salirse de las normas corrientes embarazaban a los "expertos y venerables maestros", pero que los alumnos m�s l�cidos, todav�a no embotados por el estudio rutinario, resolv�an con facilidad. Entre dichos problemas (Petrov discurri� varios) estaba el de los segadores. Los maestros con experiencia, claro, pod�an resolverlo con facilidad mediante ecuaciones, pero no daban con su sencilla resoluci�n aritm�tica. Sin embargo, el problema es tan f�cil que para resolverlo en absoluto no merece la pena servirse del �lgebra.
Si el prado mayor fue segado por todo el personal del artel en medio d�a, y por la mitad de la gente en el resto de la jornada, es natural que medio artel seg� en medio d�a 1 / 3 del prado. Por consiguiente, en el prado menor quedaba sin segar1 / 2 - 1 / 3 = 1 / 6
Si un trabajador siega en un d�a 1 / 6 del prado, y si fue segado 6 / 6 + 2 / 6 = 8 / 6, esto quiere decir que hab�a 8 segadores.
Tolst�i, aficionado de siempre a los problemas que se resuelven utilizando alg�n subterfugio y ofrecen cierta dificultad, conoc�a desde la juventud �ste, de los segadores, gracias a mi padre. Cuando tuve ocasi�n de hablar de dicho problema con Tolst�i, ya anciano, le agradaba, sobre todo, el hecho de que el problema se hace m�s comprensible si, al resolverlo, se emplea este sencillo diagrama (fig. 7)".
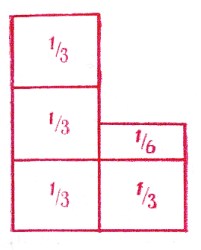
|
| Figura 7. |
Ofrecemos a continuaci�n algunos problemas que, con cierta imaginaci�n, son m�s f�ciles de resolver por medio de la aritm�tica que vali�ndose del �lgebra.
Volver
8. Las vacas en el prado
Problema
"Al estudiar las ciencias, los ejercicios son m�s �tiles que las reglas",escrib�a Newton en su Aritm�tica Universal, y acompañaba las indicaciones te�ricas con una serie de ejemplos. Entre ellos hallamos el de los toros que pastan en el prado, que gener� un tipo espec�fico de problemas semejantes a �ste:
"La hierba crece en todo el prado con igual rapidez y espesura. Se sabe que 70 vacas se la comer�an en 24 d�as, y 30, en 60 d�as. �Cu�ntas vacas se comer�an toda la hierba en 96 d�as?".
Este problema sirvi� de argumento para un cuento humor�stico, que recuerda el Maestro particular de Ch�jov. Dos adultos, familiares del escolar a quien hab�an encargado resolver este problema, se esforzaban in�tilmente por hallar su soluci�n y se asombraban:
- �Qu� extraño es el resultado! - diijo uno - . Si en 24 d�as 70 vacas se comen la hierba, entonces, �cu�ntas vacas se la comer�n en 96 d�as? Claro que 1 / 4 de 70, es decir, 17 1 / 2 vacas... �Este es el primer absurdo! El segundo todav�a m�s extraño, es que si 30 vacas se comen la hierba en 60 d�as, en 96 se la comer�n 18 3 / 4 vacas. Adem�s, si 70 vacas se comen la hierba en 24 d�as,
30 vacas emplean en ello 56 d�as, y no 60, como afirma el problema.
- �Pero tiene usted en cuenta que la hierbaa crece sin cesar? - pregunt� otro.
La observaci�n era razonable; la hierba crece incesantemente, circunstancia que no puede echarse en olvido, pues en ese caso no s�lo no puede resolverse el problema, sino que sus mismas condiciones parecer�n contradictorias.
�C�mo debe resolverse pues, el problema?
Soluci�n
Introduzcamos tambi�n aqu� una segunda inc�gnita, que representar� el crecimiento diario de la hierba, expresado en partes de las reservas de la misma en el prado. En una jornada hay un crecimiento de y ; en 24 d�as ser� 24 y . Si tomamos todo el pasto como 1, entonces, en 24 d�as las vacas se comer�n
En una jornada las 70 vacas comer�n
y una vaca (de las 70) comer�
Siguiendo el mismo razonamiento: si 30 vacas acaban con toda la hierba del prado en 60 d�as, una vaca comer� en un d�a
Pero la cantidad de hierba comida por una vaca en un solo d�a es igual para los dos rebaños. Por eso
de donde
Cuando se halla y (medida de crecimiento) es ya f�cil determinar qu� parte de la reserva inicial se come una vaca al d�a
Por �ltimo establecemos la ecuaci�n para la soluci�n definitiva del problema: si el n�mero de vacas es x , entonces,
de donde x = 20
20 vacas se comer�an toda la hierba en 96 d�as.
Volver
9. El problema de Newton
Examinemos ahora un problema del mismo tipo que el anterior: el problema de Newton acerca de los toros.
El problema, en realidad, no fue ideado por Newton, sino que es de origen popular.
Problema
"Tres prados cubiertos de hierba de una misma espesura y con el mismo grado de crecimiento, tienen un �rea de 3 1 / 3 Ha, 10 Ha y 24 Ha. La hierba del primero es comida por 12 toros durante 4 semanas; la del segundo, por 21 toros durante 9 semanas. �Cu�ntos toros comer�n la hierba del tercero durante 18 semanas?"
Soluci�n
Introducimos la inc�gnita auxiliar y , que significa la parte de la reserva inicial de hierba que crece en 1 Ha durante una semana. En el primer prado crece durante la primera semana una cantidad de hierba iguala 3 1 / 3 y ; durante 4 semanas, 3 1 / 3 y * 4 = (40 / 3)* y de la reserva de hierba que hab�a inicialmente en 1 Ha. Esto equivale a un crecimiento del �rea inicial del prado igual a:
hect�reas. En otras palabras: los toros comen tanta hierba como se precisa para cubrir un prado de {3 1 / 3 + (40 / 3) y } hect�reas. En una semana 12 toros se comen un cuarto de esta cantidad, y un toro come en una semana 1 / 48, es decir, la reserva de hierba que hay en un �rea de
De esa misma manera, con los datos del segundo prado, hallamos el �rea de �ste que alimenta a un solo toro durante una semana:
|
crecimiento de la hierba en 1 Ha durante 1 semana = y crecimiento de la hierba en 1 Ha durante 9 semanas = 9 y crecimiento de la hierba en 10 Ha durante 9 semanas = 90 y |
La superficie del sector que contiene hierba suficiente para alimentar 21 toros durante 9 semanas es igual a
El �rea necesaria para mantener un toro durante una semana ser�:
hect�reas. Ambas normas de alimentaci�n deben ser id�nticas:
Al despejar la inc�gnita encontramos que y = 1 / 12. Veamos ahora cu�l debe ser el �rea del prado con hierba suficiente para mantener un toro durante una semana:
hect�reas. Ocup�monos, por �ltimo, de la pregunta del problema. Si representamos el n�mero desconocido de toros con la x , tendremos:
de donde x = 36.
El tercer prado puede mantener 36 toros durante 18 semanas.
Volver
10. El cambio de las manecillas del reloj
Problema
A. Moshkovski, bi�grafo y amigo del famoso f�sico Albert Einstein, en su deseo de distraer a �ste durante su enfermedad, le propuso resolver el problema siguiente (fig. 8):
"Tomemos un reloj - dijo Moshkovski - que tenga las saetas en las 12. Si en esta posici�n el minutero y el horario cambiaran de funci�n, la hora marcada ser�a la misma; pero a otras horas, por ejemplo, a las 6 esa permuta de las saetas dar�a lugar a un absurdo, a una situaci�n que, en un reloj que marchara normalmente no podr�a producirse; el minutero no puede hallarse en las 6 cuando el horario se encuentra en las 12. De aqu� surge la siguiente pregunta: �Cu�ndo y cada cu�nto tiempo ocupan las manecillas de un reloj tal posici�n en la cual al cambiar �stas de funci�n entre s� se producen nuevas situaciones posibles en un reloj normal?
- S�, contest� Einstein, este problema es mmuy apropiado para un hombre obligado por su enfermedad a permanecer postrado en el lecho: despierta bastante inter�s y no es muy f�cil. Me temo, sin embargo, que la distracci�n dure poco tiempo: he dado ya con la forma de resolverlo. Se incorpor� en el lecho y con unos cuantos trazos dibuj� en un papel un esquema que reflejaba las condiciones del problema. Einstein no necesit� para resolverlo m�s tiempo que el que he empleado yo en formularlo..." �C�mo se resuelve?
Soluci�n
Midamos la distancia que recorren las manecillas, vali�ndonos de 60 divisiones de la esfera, a partir de las 12. Supongamos que en una de las posiciones buscadas, el horario se encuentra a x fracciones a partir del n�mero 12, y el minutero, a y divisiones.

|
| Figura 8 |
Como las 60 fracciones son recorridas por el horario en 12 horas, es decir, a 5 divisiones por hora, entonces, x partes de la esfera ser�n recorridas por el horario en x / 5 horas. Dicho con otras palabras, habr�n pasado x / 5 horas desde que el reloj dio las 12. El minutero recorre y fracciones en y minutos, es decir, en y / 60 horas. Expresado de otro modo: el minutero ha pasado la cifra 12 hace y / 60 o al cabo de
horas despu�s de que ambas saetas se encontraban en las doce. Este n�mero es entero (desde el cero al 11), ya que muestra cu�ntas horas completas han pasado desde las doce. Al cambiar las manecillas defunci�n encontraremos por analog�a que a partir de las doce habr�n pasado
horas completas. Este n�mero tambi�n es entero (desde el cero hasta el 11).
Planteamos el siguiente sistema de ecuaciones:
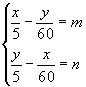
donde m y n son n�meros enteros comprendidos entre el 0 y el 11. En este sistema despejaremos las inc�gnitas:
y = {60 * (12 n + m ) / 143
Asignando a m y n un valor comprendido entre 0 y 11 determinaremos todas las posiciones requeridas de las saetas. Como cada uno de los 12 valores que tiene m , puede ser confrontado con cada uno de los 12 de n , quiz�s parezca que el n�mero de soluciones posibles puede ser 12*12 = 144; pero en realidad es igual a 143, porque cuando m = 0, n = 0, y si m = 11, n = 11, las manecilla ocupan la misma posici�n.
Cuando m = 11, n = 11 tenemos:
y = 60
es decir, las manecillas est�n en las 12, como en el caso de m = 0, n = 0.
No nos detendremos a examinar todas las posiciones posibles; ocup�monos de dos casos:
Primer caso:
m = 1, n = 1;
es decir, señala 1 hora 5 / 11 minutos; en este momento las manecillas est�n en el mismo sitio por lo que pueden cambiar de funci�n (como siempre que coincidan).
Segundo caso:
m = 8, n = 5;
y = {90 * (8 + 12 * 5)} / 143 » 28.53
Los momentos respectivos ser�n: las 8 horas y 28,53 minutos y las 5 horas 42,38 minutos.
El n�mero de soluciones, como se indic� ya, es de 143. Para llegar a los puntos de la esfera donde se encuentran las posiciones requeridas de las saetas, hay que dividir la circunferencia de la esfera en 143 partes iguales, obteniendo 143 puntos que son los que buscamos. En los espacios intermedios no hay otras posiciones semejantes de las manecillas.
Volver
11. Coincidencia de las saetas
Problema
�En cu�ntas posiciones pueden coincidir el horario y el minutero de un reloj que marche normalmente?
Soluci�n
Podemos valernos de las ecuaciones del problema anterior, ya que si las dos manecillas coinciden, pueden cambiar entre s� de funci�n sin que se produzca alteraci�n alguna. En este caso, ambas saetas habr�n recorrido el mismo n�mero de divisiones, a partir del n�mero 12; es decir, x = y . Por esta causa, los razonamientos del problema precedente nos brindan la siguiente expresi�n:
donde m es un entero comprendido entre 0 y 11. Aqu� podemos despejar la inc�gnita:
De los doce valores de m (del 0 al 11) obtenemos en lugar de 12, s�lo 11 posiciones diversas de las manecillas, toda vez que siendo m = 11 vemos que x = 60; es decir, ambas saetas han recorrido 60 divisiones y se hallan en la cifra 12; esto mismo sucede cuando m = 0.
Volver
12. El arte de adivinar n�meros
Cada uno de Uds. se encontraba indudablemente con "prestidigitadores" que pueden adivinar n�meros. Como regla un prestidigitador propone realizar operaciones del siguiente car�cter: pensar un n�mero cualquiera, adicionar 2, multiplicar el resultado por 3, restar 5, restar el n�mero pensado etc., en total cinco o una decena de operaciones. Luego el prestidigitador pide que le comuniquen el resultado y, al obtener la respuesta, en seguida comunica el n�mero pensado.
Claro est� que el secreto de la "prestidigitaci�n" es muy f�cil y se basa en las mismas ecuaciones.
Supongamos que el prestidigitador le haya propuesto a Ud. realizar un programa de operaciones indicado en la columna izquierda de la tabla siguiente:
| piense un n�mero | x |
| adicione 2 | x + 2 |
| el resultado multipl�quelo por 3 | 3x + 6 |
| reste 7 | 3x - 1 |
| reste el n�mero pensado | 2x + 1 |
| multiplique por 2 | 4x + 2 |
| reste 1 | 4x + 1 |
Luego el prestidigitador pide que le comuniquen el resultado final y, al obtenerlo, dice al instante el n�mero pensado. �C�mo lo hace?
Para comprender esto, hay que mirar la columna derecha de la tabla, donde las indicaciones del prestidigitador est�n traducidas al idioma del �lgebra. Mirando esta columna se puede comprender, que si Ud. ha pensado cualquier n�mero x, entonces realizadas todas las operaciones se obtendr� 4x - 1. Conociendo este resultado no es dif�cil "adivinar" el n�mero.
Supongamos, por ejemplo, que Ud. haya dicho al prestidigitador que el resultado es 33. Entonces el prestidigitador resuelve mentalmente muy r�pido la ecuaci�n 4x � 1 = 33 y obtiene la respuesta: x = 8. Es decir, hace falta restar 1 del resultado final (33 - 1 = 32) y luego el n�mero obtenido se divide entre 4 (32 : 4 = 8). El resultado de esta divisi�n es el n�mero pensado (8). Si el resultado final es 25, entonces el prestidigitador hace mentalmente las siguientes operaciones 25 � 1 = 24, 24 / 4 = 6 y le comunica que Ud. ha pensado el n�mero 6.
Como se ve todo es muy f�cil. El prestidigitador sabe de antemano qu� hace falta hacer con el resultado para obtener el n�mero pensado.
Despu�s de comprender esto Ud. puede asombrar y desconcertar a�n m�s a sus amigos proponi�ndoles a ellos mismos escoger seg�n su propio parecer, el car�cter de operaciones sobre un n�mero pensado. Ud. propone a su amigo pensar un n�mero y realizar en cualquier orden operaciones del car�cter siguiente: sumar o restar un n�mero conocido (por ejemplo: sumar 2, restar 5, etc.), multiplicar por un n�mero conocido (por 2, por 3, etc.), sumar o restar el n�mero pensado. Su amigo, para embrollarle, va a amontonar una serie de operaciones. Por ejemplo, �l ha pensado el n�mero 5 (el n�mero pensado no se le comunica a Ud.) y realizando operaciones le dice:
- he pensado un n�mero, lo he multiplicado por 2, al resultado he sumado 3, luego he sumado el n�mero pensado, al resultado he sumado 1, todo lo he multiplicado por 2, he restado el n�mero pensado, luego he restado 3, una vez m�s he restado el n�mero pensado, he restado 2. Por fin, el resultado lo he multiplicado por 2 y he sumado 3.
Al decidir que �l le ha embrollado por completo �l comunica a Ud. con el aspecto triunfante:
- el resultado final es 49.
Para su asombro Ud. le comunica inmediatamente que �l ha pensado el n�mero 5.
�C�mo lo hace Ud.? Ahora todo eso es bastante claro. Cuando su amigo le comunica las operaciones que �l est� realizando con el n�mero pensado, Ud. a la vez act�a mentalmente con la inc�gnita x . El le dice: "He pensado un n�mero...", Ud. repite mentalmente: "entonces tenemos x ". El dice: "...lo he multiplicado por 2..." (�l de veras realiza la multiplicaci�n de n�meros), Ud. prosigue mentalmente; "...ahora tenemos 2 x ". El dice: "...al resultado he sumado 3...", Ud. le sigue inmediatamente: 2 x + 3 etc. Cuando �l le "ha embrollado" completamente y ha realizado todas las operaciones mencionadas arriba, Ud. ha llegado al resultado indicado en la tabla siguiente (en la columna izquierda est� escrito todo lo dicho en voz alta por su amigo y en la derecha - las operaciones que Ud. ha hecho mentalmente):
| He pensado un n�mero | x |
| lo he multiplicado por 2 | 2x |
| al resultado he sumado 3 | 2x + 3 |
| luego he sumado el n�mero pensado | 3x + 3 |
| ahora he sumado 1 | 3x + 4 |
| el resultado lo he multiplicado por 2 | 6x + 8 |
| he restado el n�mero pensado | 5x + 8 |
| he restado 3 | 5x + 5 |
| m�s he restado el n�mero pensado | 4x + 5 |
| he restado 2 | 4x + 3 |
| por fin, el resultado lo he multiplicado por 2 | 8x + 6 |
| y he sumado 3 | 8x + 9 |
Ud. ha pensado por �ltimo: el resultado final es 8 x + 9. Ahora �l dice: "El resultado final es 49". Ud. tiene ya la ecuaci�n hecha: 8 x + 9 = 49. Resolverla es una futilidad y Ud. le comunica en el acto que �l ha pensado el n�mero 5. Esta prestidigitaci�n es particularmente impresionante porque las operaciones que hace falta realizar con el n�mero pensado no las propone Ud., sino su amigo las "inventa".
Sin embargo, hay un caso cuando la prestidigitaci�n no tiene �xito. Si Ud. despu�s de realizar (contando mentalmente) una serie de operaciones ha obtenido, por ejemplo, x + 14, y su amigo dice luego: "...ahora he restado el n�mero pensado y el resultado final es 14". Ud. le sigue ( x + 14) - x = 14, de verdad resulta 14, pero no hay ninguna ecuaci�n y por eso Ud. no puede adivinar el n�mero pensado. �Qu� es necesario hacer en este caso? Obre as�: tan pronto Ud. tenga el resultado que no contiene la inc�gnita x, interrumpa a su amigo, dici�ndole: "�Pare! Ahora puedo sin preguntar nada comunicarte el resultado que tienes. Es 14". Esto de veras va a desconcertar a su amigo, pues �l no le ha dicho completamente nada. A pesar de que Ud. no supo adivinar el n�mero pensado, la prestidigitaci�n ha resultado espl�ndida.
He aqu� un ejemplo m�s (como antes en la columna izquierda se encuentra lo dicho por su amigo):
| He pensado un n�mero | x |
| a este n�mero he sumado 2 | x + 2 |
| el resultado lo he multiplicado por 2 | 2x + 4 |
| ahora he sumado 3 | 2x + 7 |
| he restado el n�mero pensado | x + 7 |
| he sumado 5 | x + 12 |
| luego he restado el n�mero pensado | 12 |
En el momento cuando el resultado ha sido 12, es decir, es una f�rmula que no tiene m�s la inc�gnita x , Ud. interrumpe al amigo comunic�ndole que ahora el resultado es 12.
Despu�s de practicar un poco Ud. podr� f�cilmente mostrar a sus amigos semejantes "prestidigitaciones".
Volver
13. Un supuesto absurdo
Problema
He aqu� un problema que puede parecer incongruente: �Cu�l es la equivalencia de 84 si
Esta ins�lita pregunta est� muy lejos de carecer de sentido, y puede ser resuelta mediante ecuaciones.
Pruebe a descifrarla.
Soluci�n
Probablemente habr�n comprendido que los datos del problema no pertenecen al sistema decimal, pues en caso contrario, la pregunta "�Cu�l es la equivalencia de 84?" ser�a un absurdo. Supongamos que la base del sistema desconocido de numeraci�n es x . El n�mero "84" equivale entonces a 8 unidades de segundo orden y 4 unidades del primero, es decir
El n�mero "54" equivale a
Tenemos, por lo tanto, la ecuaci�n
es decir, en el sistema de numeraci�n decimal ser�a
de donde x = 12.
Este n�mero est� expresado en el sistema de base 12, y "84" = 8 * 12 + 4 = 100. Por lo tanto, si 8 * 8 = "54", "84" ser� igual a 100.
De esta misma manera se resuelve otro de los problemas de este tipo: �Cu�l es el equivalente de 100, si 5 * 6 = 33?
Respuesta: 81 (sistema de base 9).
Volver
14. La ecuaci�n piensa por nosotros
Si no cree que las ecuaciones son a veces m�s previsoras que nosotros mismos resuelva este problema:
El padre tiene 32 años; el hijo, 5. �Al cabo de cu�ntos años ser� la edad del padre diez veces mayor que la del hijo?
Expresemos el tiempo buscado con x . Al cabo de x años el padre tendr� 32 + x años; y el hijo, 5 + x años. Y como el padre debe tener 10 veces m�s años que el hijo, se establece la ecuaci�n
Al resolverla hallamos que
"Al cabo de menos 2 años" significa "hace dos años". Al plantear la ecuaci�n no pens�bamos que en el futuro la edad del padre no ser�a nunca 10 veces superior a la del hijo; esa correlaci�n pudo tener lugar s�lo en el pasado. La ecuaci�n ha sido m�s reflexiva que nosotros, y nos ha recordado nuestro descuido.
Volver
15. Curiosidades y sorpresas
Hay ocasiones en las que al resolver las ecuaciones tropezamos con soluciones que pueden desconcertar a un matem�tico poco ducho. Veamos algunos ejemplos:
I. Hallar un n�mero de dos cifras que tenga las siguientes propiedades:
La cifra de las decenas debe ser 4 unidades inferior a la cifra de las unidades. Si ese mismo n�mero se escribe invirtiendo el lugar de sus cifras y se le sustrae el n�mero buscado, se obtiene 27. Expresando el guarismo de las decenas con la x, y el de las unidades con la y, formaremos f�cilmente el siguiente sistema de ecuaciones para este problema:

Si el valor que tiene x en la primera ecuaci�n se coloca en la segunda, resultar� que
al operar tendremos que
No se ha hallado el valor de las inc�gnitas, pero se ha visto que 36 = 27... �qu� quiere decir esto? Esto significa que no existe ning�n n�mero compuesto de dos cifras que responda a las condiciones del problema, y que las ecuaciones planteadas se contradicen mutuamente. En efecto, multipliquemos ambos miembros de la primera igualdad por 9 y tendremos:
y de la segunda ecuaci�n (despu�s de abrir los par�ntesis y reducir los t�rminos semejantes) resulta:
Seg�n la primera ecuaci�n 9y - 9x es igual a 36 y de acuerdo con la segunda equivale a 27. Esto es a todas luces imposible, por cuanto 36 ¹ 27. Una confusi�n an�loga espera a quien resuelva el siguiente sistema de ecuaciones:
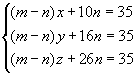
Al dividir la primera ecuaci�n por la segunda obtendremos:
y si confrontamos la ecuaci�n obtenida con la segunda del sistema veremos que
x * y = 2
es decir, que 4 = 2. No hay cifras que satisfagan las condiciones de este sistema.
(Sistemas de ecuaciones, semejantes a los que acabamos de examinar que no pueden ser resueltos, se llaman no combinados.)
II. Si cambiamos un tanto las condiciones del problema anterior recibiremos otra sorpresa. Supongamos que la cifra de las decenas es menor en 3 unidades que la cifra de las unidades. Las dem�s condiciones del problema permanecen invariables �Cu�l ser� este n�mero? Planteemos la ecuaci�n. Si expresamos la cifra de las decenas con la x , la de las unidades ser� x + 3. Traduzcamos el problema al idioma del �lgebra:
Al reducir se obtiene 27 = 27.
Esta igualdad es incuestionable, pero nada nos dice de la ra�z de x �Significa esto que no existe ning�n valor que responda a las condiciones del problema?
Por el contrario. Esto se debe a que la igualdad dada es una identidad, es decir, que es cierta cualquiera que sea la magnitud de la inc�gnita x . En efecto, las condiciones del problema son v�lidas para todo n�mero compuesto de dos cifras siempre que el guarismo de las unidades sea mayor en 3 unidades que el de las decenas:
47 + 27 = 74
25 + 27 = 52
58 + 27 = 85
36 + 27 = 63
69 + 27 = 96.
III. Hallar un n�mero de tres cifras que responda a las siguientes condiciones:
- La cifra de las decenas sea 7;
- La cifra de las centenas sea inferior en 4 unidades a la cifra de las unidades;
- Si las cifras del mismo se colocan en orden inverso, el nuevo n�mero ser� 396 unidades mayor que el buscado.
Despu�s de reducida esta ecuaci�n se llega a la igualdad 396 = 396.
Los lectores conocen ya c�mo hay que interpretar los resultados de este tipo. Esto significa que un n�mero de tres cifras, en el que la primera es menor que la tercera en 4 unidades, aumenta en 396 si se le coloca en orden inverso.
Hasta ahora hemos examinado problemas que tienen un car�cter m�s o menos artificioso y te�rico; su misi�n consiste en contribuir a que se adquiera h�bito en el planteamiento y la soluci�n de ecuaciones. Ahora, pertrechados te�ricamente, ofreceremos algunos ejemplos relacionados con la producci�n, la vida cotidiana, y la actividad militar y deportiva.
Volver
16. En la peluquer�a
Problema
�Puede el �lgebra tener alguna aplicaci�n en la peluquer�a? Resulta que puede darse esa circunstancia. Me convenc� de ello en cierta ocasi�n, cuando encontr�ndome en un establecimiento de esa clase, se dirigi� a m� un oficial con una inesperada petici�n:
- �No podr� resolvernos usted un problema qque no sabemos c�mo hacerlo? - �No se imagina cu�nta agua oxigenada hemos echado a perder por esa causa! - agreg� otro.
- �De qu� se trata? - pregunt�.
- Tenemos dos soluciones de agua oxigenada:: al 30% una, y al 3% ]a otra. Debemos mezclarlas de tal forma que obtengamos una soluci�n al 12%. Pero no podemos hallar las proporciones correspondientes...
Me dieron un papel y encontr� la proporci�n que buscaban. Result� ser un problema muy f�cil.
Soluci�n
El problema puede ser resuelto tambi�n por v�a aritm�tica, pero mediante el �lgebra se obtiene el resultado con m�s sencillez y prontitud. Supongamos que para formar la mezcla al 12% hay que tomar x gramos de soluci�n al 3% e y gramos al 30% . Siendo as�, la primera porci�n contendr� 0,03 x gramos de agua oxigenada pura y , la segunda, 0,3 y; en total habr�
Con esto resultar� ( x + y ) gramos de soluci�n, en la que el agua oxigenada pura ser�
Tenemos la ecuaci�n
De esta ecuaci�n hallamos: x = 2 y , es decir, que deber� tomarse doble cantidad de soluci�n al 3% que la empleada del 30%.
Volver
17. El tranv�a y el peat�n
Problema
Cuando marchaba a lo largo de la l�nea del tranv�a observ� que cada 12 minutos me alcanzaba uno de esos veh�culos, y cada 4 minutos otro de ellos pasaba en direcci�n contraria. Tanto los veh�culos como yo nos desplaz�bamos con velocidad constante
�Cada cu�ntos minutos sal�an los tranv�as de las estaciones terminales?
Soluci�n
Si los tranv�as sal�an cada x minutos, eso quiere decir que por aquel lugar donde yo me encontraba con un tranv�a ten�a que pasar el siguiente despu�s de x minutos. Si el veh�culo iba en mi direcci�n, entonces en 12 - x minutos deb�a recorrer el camino que yo hac�a en 12 minutos. Eso significa que el camino que yo andaba en un minuto el tranv�a lo hac�a en
Si el tranv�a iba en direcci�n contraria nos cruzar�amos 4 minutos despu�s de haberme encontrado con el anterior, y en el tiempo restante ( x - 4) minutos deb�a recorrer el camino hechoo por m� en esos 4 minutos. Por lo tanto, el camino que yo andaba en 1 minuto lo hac�a el tranv�a en ( x � 4) / 4 minutos. Tenemos pues la ecuaci�n
De donde se deduce que x = 6. Cada 6 minutos iniciaban los tranv�as su itinerario.
Puede proponerse la siguiente resoluci�n (en esencia es una soluci�n aritm�tica). Expresemos la distancia que separaba a los tranv�as entre s� con la letra a . Entonces la distancia que mediaba entre el tranv�a que iba a mi encuentro y yo, disminu�a en a / 4 cada minuto (por cuanto la distancia entre el tranv�a que acababa de pasar y el siguiente, igual a a , la recorr�amos en 4 minutos). Si el tranv�a iba en mi direcci�n, la distancia entre nosotros se reduc�a cada minuto en a /12. Supongamos que yo marchara hacia delante durante un minuto y, despu�s, anduviera otro minuto hacia atr�s (es decir, regresara al punto de partida). En este caso la distancia que mediaba entre el tranv�a - que iba a mi encuentro - disminu�a durante el primer minuto en a / 4 , y en el segundo minuto, en a / 12. En consecuencia, en el lapso de 2 minutos, la distancia entre nosotros se reduc�a en a / 4 + a / 12 = a / 3. Lo mismo habr�a ocurrido si yo hubiera permanecido inm�vil en el sitio, ya, que, en fin de cuentas, volver�a hacia atr�s. De esta manera, si yo no hubiera avanzado, en un minuto (no en dos) el tranv�a se hubiese acercado hacia m� a / 3 : 2 = a / 6 , y toda la distancia a la habr�a recorrido en 6 minutos. Por ello, para un observador inm�vil, los tranv�as pasaban con intervalos de 6 minutos.
Volver
18. El barco y la balsa
Problema
Un barco se desplaza 5 horas sin interrupci�n r�o abajo desde la ciudad A a la ciudad B. De vuelta avanza contra la corriente (con su marcha ordinaria y sin detenerse) durante 7 horas. �Cu�ntas horas necesitar� una balsa para desplazarse de la ciudad A a la B, yendo a la misma velocidad de la corriente?
Soluci�n
Expresemos con x el tiempo (en horas) que necesita el barco para recorrer la distancia que separa A de B en el agua estancada (es decir, con la velocidad del barco) y con y, el tiempo que se desliza la balsa. Siendo as�, en una hora el barco recorre 1 / x de la distancia AB, y la balsa (al igual que la corriente) 1 / y de esta distancia. Por esta raz�n, el barco, marchando impulsado por la corriente, en una hora recorre 1 / x + 1 / y de la distancia AB, y hacia arriba (contra la corriente) 1 / x � 1 / y . Por las condiciones del problema se deduce que hacia abajo el barco hace en una hora 1 / 5 de la distancia, y, hacia arriba, 1 / 7 . De aqu� el sistema:
1 / x � 1 / y = 1 / 7
Observamos que para solucionar este sistema no debemos hacer desaparecer los denominadores: es suficiente con restar la segunda ecuaci�n de la primera. Operando resultar�:
de donde y = 35. Las balsas se deslizar�n desde A hasta B en 35 horas.
Volver
19. Dos botes de caf�
Problema
Dos botes llenos de caf� tienen la misma forma y est�n hechos de la misma hojalata. El primero pesa 2 kg y tiene 12 cm de altura; el segundo pesa 1 kg y mide 9,5 cm de altura. �Cu�l es el peso neto del caf� en los dos botes?
Soluci�n
Expresemos el peso del contenido del bote grande con x , y el del pequeño con y . El peso de los botes lo expresaremos con z y t respectivamente. De donde se obtienen las siguientes ecuaciones:
y + t = 1
Teniendo en cuenta que los pesos del contenido de ambos botes repletos se relacionan entre s� como sus propios vol�menes es decir, como el cubo de sus alturas, resulta que
�
El peso de los botes vac�os se relaciona entre s� como se relacionan sus superficies completas, es decir, como los cuadrados de sus alturas. Por ello
�
Sustituyendo los valores de x y de z en la primera ecuaci�n resultar� el sistema
y + t = 1
Al resolverlo tendremos:
t = 0.05
Por lo tanto, x = 1,92, z = 0,08.
El peso del caf� sin el envase ser�: el del bote grande, 1,92 kg; el del pequeño, 0,94 kg.
Volver
20. Velada
Problema
A una velada asistieron 20 personas. Mar�a bail� con siete muchachos; Olga, con ocho; Vera, con nueve, y as� hasta llegar a Nina, que bail� con todos ellos. �Cu�ntos muchachos hab�a en la velada?
Soluci�n
La soluci�n del problema es muy sencilla si se elige con acierto la inc�gnita. Busquemos el n�mero de las j�venes, que expresaremos con la x :
| 1 a | Mar�a bail� con | 6 + 1 | muchachos |
| 2� | Olga bail� con | 6 + 2 | muchachos |
| 3� | Vera bail� con | 6 + 3 | muchachos |
| ... | ... | ... | ... |
| x a | Nina bail� con | 6 + x | muchachos |
Establezcamos la siguiente ecuaci�n:
de donde x = 7, por lo tanto, el n�mero de muchachos era 20 - 7 = 13.
Volver
21. Exploraci�n marina
Primer problema
El explorador (la nave de reconocimiento), que marchaba con el resto de la escuadra, recibi� la tarea de explorar el mar en una zona de 70 millas en la direcci�n en que marchaba la escuadra. La velocidad de �sta era de 35 millas por hora; la del barco explorador, de 70 millas por hora. �Cu�nto tiempo tardar� �ste en incorporarse de nuevo a la escuadra?
Soluci�n
Designemos el n�mero de horas buscadas con la x . Durante este tiempo la escuadra recorri� 35 x millas; y la nave de reconocimiento, 70 x . Esta naveg� 70 millas hacia adelante y una parte de esta ruta al regreso; la otra parte fue hecha por el resto de la escuadra. Todos juntos recorrieron 70 x + 35 x , lo que es iguala 2 * 70 millas. De aqu� la ecuaci�n
de donde
La embarcaci�n exploradora se incorpor� a la escuadra, aproximadamente, al cabo de hora 20 minutos.
Segundo problema
El barco explorador recibi� la orden de hacer el reconocimiento en la direcci�n que llevaba la escuadra. Tres horas despu�s, la nave deb�a incorporarse a la escuadra. �Al cabo de cu�nto tiempo, a partir del momento en que s� distancia de la escuadra, debe iniciar el barco explorador el regreso, si su velocidad es de 60 nudos, y la de la escuadra de 40 nudos?
Soluci�n
Supongamos que la nave de reconocimiento deb�a volver al cabo de x horas; eso significa que se alej� de la escuadra x horas, y march� de vuelta, a su encuentro, 3 - x horas. Mientras todos los barcos marchaban en una misma direcci�n, en x horas pudo la embarcaci�n exploradora alejarse a una distancia igual a la diferencia entre las distancias recorridas por cada uno, es decir, en
Cuando regres� el explorador hab�a cubierto, en direcci�n a la escuadra, una distancia de 60 * (3 - x ), en tanto que la escuadra hab�a recorrido 40 * (3 - x ). Uno y otra recorrieron juntos 10 x . Por lo tanto
de donde
El explorador tuvo que modificar el rumbo, iniciando el regreso, al cabo de 2 horas y 30 minutos a partir del momento en que abandon� la escuadra.
Volver
22. En el vel�dromo
Problema
Dos ciclistas corren por el vel�dromo a velocidades constantes. Al llevar direcciones opuestas se encuentran cada 10 segundos; cuando van en la misma direcci�n, un ciclista alcanza al otro cada 170 segundos, �Cu�l es la velocidad que desarrolla cada ciclista si la longitud de la pista es de 170 m?
Soluci�n
Si la velocidad del primer ciclista es x , en 10 segundos habr� recorrido 10 x metros. El segundo (yendo al encuentro) recorre el resto de la vuelta en el intervalo que media entre dos cruces, es decir, 170 - 10 x metros. Si la velocidad del segundo es y , esto constituye 10 y metros; por lo tanto
Si los ciclistas marchan uno tras otro, en 170 segundos el primero recorre 170 x metros, y el segundo, 170 y metros. Si el primero marcha m�s de prisa que el segundo, de un encuentro al otro corre una vuelta m�s que el segundo, es decir,
Al simplificar �stas ecuaciones, tenemos:
x � y = 1
de donde x = 9, y = 8 (metros por segundo).
Volver
23. Carrera de motocicletas
Problema
En una carrera de motocicletas, tres m�quinas salieron simult�neamente. La segunda hace 15 km por hora menos que la primera, y 3 km m�s que la tercera y llega a la meta 12 minutos despu�s que la primera y 3 minutos antes que la tercera. Durante el recorrido no se registraron paradas.
Hay que determinar:
a. La distancia de la carrera,
b. La velocidad de cada motocicleta y
c. El tiempo empleado por cada m�quina.
Soluci�n
Aunque las inc�gnitas llegan a siete, se emplean s�lo dos para resolver el problema. Formemos un sistema de dos ecuaciones con dos inc�gnitas.
Expresando la velocidad de la segunda moto con la x , la velocidad de la primera ser� x + 15, y la de la tercera x - 3. La distancia se expresa con la y . En este caso la duraci�n de la carrera fue:
para la primera motocicleta y / ( x + 15)
para la segunda motocicleta y / x
para la tercera motocicleta y / ( x � 3)
La segunda m�quina hizo el recorrido en 12 minutos (1 / 5 de hora) m�s que la primera. Por ello
La tercera emple� en la carrera 3 minutos (1 / 20 de hora) m�s que la segunda. Por consiguiente,
Multiplicando por 4 esta ecuaci�n y rest�ndola de la anterior, se obtiene:
Dividimos todos los t�rminos por y ( y ¹ 0) y quitamos los denominadores, con lo que se obtiene:
y al abrir par�ntesis y reducir los t�rminos semejantes, resultar�:
de donde x = 75. Conociendo la x se obtiene el valor de la y en la primera ecuaci�n.
de donde y = 90.
De aqu� que la velocidad de las motocicletas sea: 90, 75 y 72 km por hora. La distancia ser� de 90 km.
Dividiendo la distancia por la velocidad de cada motocicleta se obtiene el tiempo invertido por cada m�quina:
la primera: 1 hora
la segunda: 1 hora y 12 minutos
la tercera: 1 hora y 15 minutos
De esta forma se ha encontrado el valor de las siete inc�gnitas.
Volver
24. Velocidad media
Problema
Un autom�vil cubri� la distancia entre dos ciudades a 60 km por hora e hizo el viaje de regreso a 40 km por hora. �Cu�l fue la velocidad media de su recorrido?
Soluci�n
La aparente sencillez del problema confunde a muchos. Sin pensar detenidamente en �l, hallan la media aritm�tica de 60 y 40, es decir, la semisuma
Esta "simple" soluci�n ser�a cierta si la ida y la vuelta hubieran durado el mismo tiempo. Pero es evidente que el recorrido de vuelta (a menos velocidad) requiere m�s tiempo que la ida. Si tenemos esto en cuenta, veremos que la respuesta de 50 km es err�nea.
Y as� es, en efecto. La ecuaci�n nos da otra soluci�n. No resulta dif�cil establecer la ecuaci�n si introducimos una inc�gnita auxiliar: la magnitud l , distancia entre las dos ciudades. Expresemos con x la velocidad media buscada y formemos la ecuaci�n
Comoquiera que l ¹ 0, podemos dividir la ecuaci�n por l , obteniendo,
de donde
De esta forma vemos que la respuesta acertada no es 50, sino 48 km por hora. Si resolvi�ramos este mismo problema con letras (en la ida, el autom�vil marchaba a una velocidad de a por hora, y de vuelta, a b por hora y obtendr�amos la ecuaci�n
de donde al despejar la x resultar�
Esto se denomina media harm�nica de las magnitudes a y b . Por lo tanto, la velocidad media del recorrido se expresa, no con la media aritm�tica, sino con la media harm�nica de las velocidades. Para a y b ; positivas, la media harm�nica ser� siempre menor que la media aritm�tica (a + b ) / 2, como se ha visto en el ejemplo num�rico (48 < 50).
Volver
25. M�quinas de c�lculo r�pido
Al tratar de las ecuaciones, Algebra Recreativa no puede desentenderse de la soluci�n de ecuaciones en m�quinas de calcular. Ya se ha dicho que las calculadoras pueden "jugar" al ajedrez (o a las damas). Adem�s pueden realizar tambi�n otras funciones; por ejemplo, la traducci�n, la orquestaci�n de melod�as, etc. Basta con elaborar el "programa" correspondiente, con arreglo al cual debe actuar la m�quina.
Claro que no vamos a examinar aqu� "programas" para el ajedrez ,o para la traducci�n, que son dif�ciles en extremo. Examinaremos tan s�lo dos "programas" sencillos. Mas en principio hay que decir algunas palabras sobre la construcci�n de la m�quina de c�lculo.
En el cap�tulo primero se ha tratado de dispositivos que permiten hacer miles y decenas de miles de operaciones por segundo. La parte de la m�quina que sirve para la ejecuci�n directa de operaciones se llama aritm�metro . Adem�s, la m�quina tiene un dispositivo de direcci�n (que regula el trabajo de toda la m�quina) y el dispositivo de memoria. La "memoria", es un dep�sito de n�meros y signos convencionales. Por �ltimo, la m�quina est� equipada con dispositivos de entrada y de salida destinados a introducir nuevos datos num�ricos y ofrecer los resultados definitivos. La m�quina registra estos resultados (ahora ya en el sistema decimal) en tarjetas especiales.
Es notorio que el sonido puede ser registrado en discos o en cinta, y despu�s reproducido. Pero la grabaci�n del sonido en un disco puede hacerse tan s�lo una vez: para realizar una nueva grabaci�n se precisa otro disco. La impresi�n de sonidos en magnet�fono tiene lugar de forma un tanto distinta, mediante el imantado de una cinta especial. El sonido registrado puede reproducirse las veces que sean precisas y, si la impresi�n resulta ya innecesaria, puede "desimantarse" y efectuar en ella una nueva grabaci�n. Una misma cinta puede grabarse varias veces, con la particularidad de que cada nueva grabaci�n "borra" la anterior.
El funcionamiento de la "memoria" se basa en un principio an�logo. Los n�meros y signos convencionales se registran el�ctrica, magn�tica o mec�nicamente en un tambor, una cinta u otro dispositivo. E1 n�mero grabado puede ser "le�do" en el momento oportuno; si no se necesita m�s puede ser borrado, grab�ndose otro en su lugar. La "extracci�n" y la "lectura" del n�mero o el signo convencional dura s�lo algunas millon�simas de segundo. La "memoria" puede constar de algunos miles de celdas y, cada celda, de varias decenas de elementos magn�ticos, por ejemplo. Convengamos en que para registrar los n�meros por medio del sistema de base dos, cada elemento imantado expresa el 1, y los no imantados, el 0. Supongamos, por ejemplo, que cada celda retentiva contiene 25 elementos (o como dicen, 25 �rdenes del sistema de base dos) y, adem�s, el primer elemento de la celda sirve para expresar el signo del n�mero ( + � - ), los siguientes 14 elementos sirven para imprimir la parte entera del n�mero y, los �ltimos 10, para registrar la parte decimal.

|
| Figura 9 |
En la fig. 9 se presentan esquem�ticamente dos celdas de memoria, con 25 elementos en cada una, los imantados se expresan con el signo + ; los desimantados, con el - . Examinemos la celda superior (la coma indica el lugar donde empieza la parte decimal, y la l�nea punteada separa el primer elemento - que sirve para fijar el signo - de los dem�s). En esa celda hay escrito (en el sistema de base dos) el n�mero + 1011,01, equivalente en el sistema decimal, al que estamos acostumbrados, al 11,25.
Adem�s de los n�meros, en las celdas retentivas se conservan las �rdenes que componen el "programa". Veamos en qu� consiste el sistema de �rdenes a tres direcciones. En este caso, al escribir la orden, la celda retentiva se divide en 4 partes (las l�neas de puntos en la celda inferior, fig. 9). La primera parte sirve para indicar el signo de operaci�n, que va cifrado. Por ejemplo:
Suma = operaci�n I,
sustracci�n = operaci�n II,
multiplicaci�n = operaci�n III, etc.
Las �rdenes se descifran as�: la primera parte de la celda es el n�mero de la operaci�n; la segunda y la tercera, los n�meros de las celdas (direcciones), de las cuales hay que extraer las cifras para las operaciones; la parte cuarta es el n�mero de la celda (direcci�n) adonde debe enviarse el resultado obtenido. Por ejemplo, en la fig. 9 (fila inferior) hay escritos por el sistema binario los n�meros 11, 11, 111,1011, en el sistema decimal, 3, 3, 7, 11, lo que significa la siguiente orden: la operaci�n III (multiplicaci�n) debe efectuarse con los n�meros de las celdas tercera y s�ptima y almacenar el resultado (es decir, registrarlo) en la celda und�cima.
En lo sucesivo inscribiremos n�meros y �rdenes, no con signos convencionales, como en la fig. 9, sino directamente en el sistema decimal. Por ejemplo; la orden expuesta en la serie inferior de la fig. 9, se escribe as�:
multiplicaci�n 3 7 11
Examinemos ahora dos sencillos ejemplos de programa.
Programa 1�
1. Suma 4 5 4 2. Multiplicaci�n 4 4 ®
3. OD 1
4. 0
5. 1
Veamos c�mo funciona una m�quina en cuyas cinco primeras celdas est�n almacenados los siguientes datos:
1 a orden: sumar los n�meros de las celdas 4 y 5 y enviar el resultado a la celda 4 (en sustituci�n de lo que figuraba anteriormente). Por consiguiente, la m�quina escribe el n�mero 0 + 1 = 1 en la celda 4. Despu�s de cumplida la orden, en las celdas 4 y 5 se encontrar�n los siguientes n�meros:
4. 1
5. 1
2 a orden: multiplicar el n�mero de la celda 4 por s� mismo (esto es, elevarlo al cuadrado) y registrar en la tarjeta el resultado, es decir, 1 2 (la flecha significa la salida de un resultado obtenido).
3 a orden: operaci�n de direcci�n a la celda 1. En otras palabras la orden OD significa la repetici�n de todas las �rdenes, empezando desde la primera. De forma que se ejecuta la primera orden.
l a orden: sumar los n�meros de las celdas 4 y 5, y fijar la suma de nuevo en la celda 4. En consecuencia, en la celda 4 estar� el n�mero 1 + 1 = 2:
4. 2
5. 1
2 a orden: elevar al cuadrado el n�mero de la celda 4 y el resultado, 2 2 , registrarlo en la tarjeta (la flecha indica la salida del resultado).
3 a orden: operaci�n de direcci�n a la celda 1 (es decir, volver de nuevo a la primera orden).
l a orden: el n�mero 2 + 1 = 3 enviarlo a la celda 4:
4. 3
5. 1
2 a orden: registrar en la tarjeta el valor de 3 2 .
3 a orden: operaci�n de direcci�n a la celda 1, etc.
Hemos visto c�mo la m�quina calcula sucesivamente los cuadrados de n�meros enteros y los registra en la tarjeta. Obs�rvese que no es preciso elegir cada vez el nuevo n�mero: la m�quina misma escoge uno tras otro los n�meros enteros y los eleva al cuadrado. Actuando de acuerdo con este programa la m�quina obtiene el cuadrado de todos los n�meros enteros desde 1 hasta el 10 000, en algunos segundos (o en partes de segundo). Debe hacerse notar que, en realidad, el programa para el c�lculo de los cuadrados de n�meros enteros debe ser algo m�s complejo que el mencionado m�s arriba. Esto se refiere, en particular, a la 2 a orden. Para registrar el resultado en tarjeta se requiere mucho m�s tiempo que el que precisa la m�quina para ejecutar una operaci�n. Por eso, los resultados se almacenan primero en las celdas libres de la "memoria", y s�lo despu�s ("sin precipitarse") se registran en las tarjetas. De esta suerte, el primer resultado definitivo se almacena en la celda la de la "memoria" que se encuentra libre; el segundo en la celda 2 a ; el tercero, en la 3 a , etc. En el programa simplificado expuesto anteriormente, todo ello hab�a sido omitido. Por añadidura, la m�quina no puede dedicarse durante largo tiempo al c�lculo de cuadrados pues no bastan las celdas de la "memoria", y es imposible "adivinar" cu�ndo ha obtenido la m�quina los cuadrados que necesitamos, a fin de desconectarla, (ya que la m�quina ejecuta miles de operaciones por segundo). Por esa raz�n se prev�n �rdenes especiales para detener la m�quina en el momento oportuno. Por ejemplo, el programa puede ser compuesto de tal manera que la m�quina calcule los cuadrados de todos los n�meros enteros, del 1 al 10 000, y despu�s se pare autom�ticamente. Hay tambi�n otra clase de �rdenes m�s complicadas, de las cuales no nos ocuparemos.
He aqu� qu� aspecto tiene el programa para el c�lculo de cuadrados del 1 al 10 000:
Programa I. a
1) suma 8 9 8
2) multiplicaci�n 8 8 10
3) suma 2 6 2
4) OC 8 7 1
5) stop
6) 0 0 1
7) 10 000
8) 0
9) 1
10) 0
11) 0
12) 0
�
Las dos primeras �rdenes se diferencian poco de las que se han expuesto en el programa simplificado. Despu�s de cumplir estas dos �rdenes, en las celdas 8, 9 y 10 habr� los siguientes n�meros:
8) 1
9) 1
10) 1 2
La tercera orden es muy interesante: hay que sumar el contenido de las celdas 2 y 6, registrar otra vez el resultado en la celda 2, despu�s de lo cual, ofrecer� el siguiente aspecto:
2) multiplicaci�n 8 8 11.
De aqu� que, despu�s de cumplida la 3a orden, cambia la segunda orden, mejor dicho, cambia una de las direcciones de la 2 a orden. A continuaci�n aclararemos las razones a que obedece esto. La cuarta es la operaci�n de comparaci�n (en sustituci�n de la tercera orden del programa examinado anteriormente). Esta se cumple as�: si el n�mero almacenado en la celda 8 es menor que el de la 7, la operaci�n de direcci�n la transmite a la celda l; en caso contrario, se efect�a la orden siguiente, (la 5). En nuestro caso como 1 < 10 000, la operaci�n de direcci�n se le encarga a la celda 1.
Por consiguiente, volvemos otra vez a la orden primera. Una vez cumplida �sta en la celda 8 se encontrar� el n�mero 2. La segunda orden, que se presentar� como
2) multiplicaci�n 8 8 11,
consiste en que 2 2 se env�a a la celda 11. Ahora queda claro para qu� fue cumplida anteriormente la 3 a orden: el nuevo 2 2 no puede ir a parar a la celda 10 que ya est� ocupada, sino a la siguiente. Una vez cumplidas las �rdenes l a y 2 a , tendremos los siguientes n�meros:
8) 2
9) 1
10) 1 2
11) 2 2
Despu�s de ejecutada la orden 3 a , la celda 2, aparecer� as�:
2) multiplicaci�n 8 8 12
es decir, la m�quina "se prepar�" para anotar el nuevo resultado en la celda 12. Y como en la celda 8 sigue habiendo un n�mero menor que en la 9, la 4 a orden significa que se encarga a la celda 1 la operaci�n de direcci�n.
Ahora, cumplidas ya las �rdenes l a y 2 a , obtendremos:
8) 3
9) 1
10) 1 2
11) 2 2
12) 3 2
�Hasta cu�ndo continuar� la m�quina calculando los cuadrados seg�n el programa? Hasta que en la celda 8 aparezca el n�mero 10 000, es decir, mientras no hayan sido obtenidos los cuadrados de los n�meros comprendidos entre el 1 y el 10 000. Despu�s, la 4 a orden ya no transmite la operaci�n de direcci�n a la celda 1 (por cuanto en la celda 8 habr� un n�mero no menor, sino igual al almacenado en la celda 7), es decir, despu�s de la 4 a orden, la m�quina cumple la 5 a orden: cesa de funcionar (se desconecta). Examinemos ahora un proceso m�s complicado de programaci�n para resolver sistemas de ecuaciones. Veamos un programa simplificado. Si se desea puede imaginarse el aspecto completo del programa. Supongamos el siguiente sistema de ecuaciones:
Este sistema es f�cil de resolver:

Este sistema (con los valores num�ricos de los coeficientes a, b, c, d, e, f) podr�a resolverse en menos de un minuto. La m�quina, en cambio, puede dar en un segundo la soluci�n de miles de tales sistemas de ecuaciones. Examinemos el programa correspondiente. Consideremos que han sido dados simult�neamente varios sistemas: con valores num�ricos para los coeficientes a, b, c, d, e, f, a', b', ... He aqu� el correspondiente programa:
Programa II
|
1) |
* 28 | 30 | 20 |
14) |
+ 3 | 19 | 3 |
26) |
a |
|
2) |
* 27 | 31 | 21 |
15) |
+ 4 | 19 | 4 |
27) |
b |
|
3) |
* 26 | 30 | 22 |
16) |
+ 5 | 19 | 5 |
28) |
c |
|
4) |
* 27 | 29 | 23 |
17) |
+ 6 | 19 | 6 |
29) |
d |
|
5) |
* 26 | 31 | 24 |
18) |
OD | 1 |
30) |
e |
|
|
6) |
* 28 | 29 | 25 |
19) |
6 | 6 | 0 |
31) |
f |
|
7) |
- 20 | 21 | 20 |
20) |
0 |
32) |
a' |
||
|
8) |
- 22 | 23 | 21 |
21) |
0 |
33) |
b' |
||
|
9) |
- 24 | 25 | 22 |
22) |
0 |
34) |
c' |
||
|
10) |
/ 20 | 21 | ® |
23) |
0 |
35) |
d' |
||
|
11) |
/ 22 | 21 | ® |
24) |
0 |
36) |
e' |
||
|
12) |
+ 1 | 19 | 1 |
25) |
0 |
37) |
f' |
||
|
13) |
+ 2 | 19 | 2 |
38) |
a'' |
1 a orden: plantear la multiplicaci�n de los n�meros almacenados en las celdas 28 y 30, y enviar el resultado a la celda 20. Dicho en otras palabras: en la celda 20 se almacenar� el n�mero ce.
De manera an�loga ser�n realizadas las �rdenes desde la 2 a hasta la 6 a . Despu�s de ejecutarlas, desde la celda 20 hasta la 25 encontraremos los siguientes n�meros:
20) ce
21) bf
22) ae
23) bd
24) af
25) cd
7 a orden: del n�mero de la celda 20, restar el de la 21, y el resultado, (es decir, ce - bf), volver a almacenarlo en la celda 20.
De la misma forma se cumplen las �rdenes 8� y 9 a En consecuencia, en las celdas 20, 21 y 22 aparecer�n los siguientes n�meros:
20) ce - bf
21) ae - bd
22) af - cd
Ordenes l0 a y 11 a : se forman los siguientes quebrados:(ce - bf) / (ae - bd) (af - cd) / (ae - bd)
que se registran el la tarjeta (es decir, se presentan como resultados definitivos). Estos son los valores de las inc�gnitas obtenidas del primer sistema de ecuaciones.
Como vemos, el primer sistema ha sido resuelto. �Para qu� hacen falta nuevas �rdenes? La parte siguiente del programa (desde la celda 12 hasta la 19) est� destinada a obligar a la m�quina a "pasar" al segundo sistema de ecuaciones. Veamos su proceso.

|
| Figura 10 |
Las �rdenes desde la 10 hasta 17 consisten en agregar al contenido desde la celda 1 hasta la 6 lo almacenado en la celda 19, y los resultados vuelven otra vez a las celdas desde la 1 hasta la 6. De tal manera, despu�s de cumplir la orden 17 a , las primeras seis celdas tendr�n el siguiente contenido:
1) * 34 36 20
2) * 33 37 21
3) * 32 36 22
4) * 33 35 23
5) * 32 37 24
6) * 34 35 25
Orden 18 a : operaci�n de direcci�n a la primera celda. �En qu� se diferencian las nuevas anotaciones de las primeras seis celdas de las anteriores? En que las dos direcciones primeras tienen en estas celdas los n�meros que van del 32 al 37 y no del 26 al 31, como antes. En otras palabras, la m�quina realizar� de nuevo las mismas operaciones, pero las cifras no ser�n tomadas, de las celdas 26 a la 31, sino de la 32 a la 37 donde est�n los coeficientes del segundo sistema de ecuaciones. Despu�s de resolver �ste, la m�quina pasa al tercero, etc.
Lo dicho hasta aqu� patentiza la importancia de "programar" con acierto. La m�quina, "de por s�", no "sabe" hacer nada. S�lo puede cumplir el programa que se la encomiende. Hay programas para calcular ra�ces, logaritmos y senos, para resolver ecuaciones de grados superiores, etc. Se ha indicado ya que existen programas para jugar al ajedrez, para la traducci�n de un idioma a otro, etc. Es claro que cuanto m�s dif�cil sea el problema a resolver, tanto m�s complejo ser� el programa correspondiente. Añadamos, como conclusi�n, que existe la programaci�n de programas, es decir, aqu�lla con ayuda de la cual la misma m�quina puede componer el programa para resolver el problema. Esto facilita en gran medida la programaci�n, que con frecuencia es bastante laboriosa.
Volver
|
|
|
|