Prefacio
Del prefacio del autor a la tercera edici�n rusa
1. La quinta operaci�n matem�tica
2. El idioma del �lgebra
3. En ayuda de la aritm�tica
4. Las ecuaciones de Diofanto
5. La sexta operaci�n matem�tica
6. Ecuaciones de segundo grado
7. La magnitud mayor y la menor
8. Progresiones
9. La s�ptima operaci�n matem�tica
Bajar Documento Completo
Cap�tulo Tercero
EN AYUDA DE LA ARITMETICA
Contenido:
1. Multiplicaci�n abreviada
2. Las cifras 1, 5 y 6
3. Los n�meros 25 y 76
4. N�meros infinitos
5. Compensaci�n
6. Divisibilidad por 11
7. El n�mero del autom�vil
8. Divisibilidad por 19
9. Teorema de Sof�a Germain
10. N�meros compuestos
11. Acerca de los n�meros primos
12. E1 mayor n�mero primo conocido
13. Un c�lculo muy laborioso
14. En ocasiones es preferible no recurrir al �lgebra
La aritm�tica es a menudo incapaz de demostrar categ�ricamente, con sus propios medios, la veracidad de algunas de sus afirmaciones. En tales casos tiene que remitirse a los m�todos sintetizadores del �lgebra. A este g�nero de tesis aritm�ticas, fundamentadas en el �lgebra, pertenecen, por ejemplo, muchas de las reglas empleadas en las operaciones abreviadas, las curiosas propiedades de algunos n�meros, los caracteres de la divisibilidad, etc. Este cap�tulo lo dedicamos al examen de cuestiones de este tipo.
1. Multiplicaci�n abreviada
Las personas con grandes h�bitos calculatorios facilitan con frecuencia las operaciones mediante transformaciones algebraicas poco complejas. Por ejemplo, la operaci�n 988 2 se efect�a como sigue:
Es f�cil comprender que en este caso se recurre ala siguiente transformaci�n algebraica:
a 2 = a 2 � b 2 + b 2
En la pr�ctica podemos aplicar esta f�rmula para los c�lculos mentales. Por ejemplo:
| 27 2 = | 27 + 3) * (27 - 3) + 3 2 = |
729 |
| 63 2 = | 66 * 60 + 3 2 = |
3969 |
| 18 2 = | 20 � 16 + 2 2 = |
324 |
| 37 2 = | 40 * 34 + 3 2 = |
1369 |
| 48 2 = | 50 - 46 + 2 2 = |
2304 |
| 54 2 = | 58 * 50 + 4 2 = |
2916 |
La multiplicaci�n 986 * 997 se realiza as�:
�En qu� se basa este m�todo? Supongamos a los factores en forma de:
y multipliquemos estos factores seg�n las reglas del �lgebra:
A continuaci�n siguen las transformaciones:
1000 * (1000 - 14) �1000 * 3 + 14 * 3 =
= 1000 * 986 � 1000 * 3 + 14 * 3 =
= 1000 (986 - 3) + 14 * 3
La �ltima l�nea es la que expresa el m�todo de dicho c�lculo. Ofrece inter�s el procedimiento para multiplicar dos n�meros compuestos de tres cifras, cuando el guarismo de las decenas es el mismo, y la suma de las unidades, 10.
Por ejemplo, la multiplicaci�n
se efectuar� de esta manera:
y su resultado es 616.221.
Este m�todo se deduce de las siguientes transformaciones:
(780 - 1 - 3) * (780 - 1 - 7) =
= 780 * 780 - 1 - 7803 + 780 * 7 + 3 * 7 =
= 780 * 780 + 780 * 10 + 3 * 7 =
= 780 * (780 + 10) + 3 * 7 = 780 * 790 + 21 =
= 616.200 + 21
Existe otro medio, todav�a m�s sencillo, para realizar multiplicaciones an�logas:
= 616.225 - 4 = 616.221
En este ejemplo hemos tenido que elevar al cuadrado el n�mero 785. Para elevar r�pidamente al cuadrado un n�mero acabado en 5, es muy c�modo el siguiente m�todo:
65 2 ; 6 * 7 = 42; resultado 4225
75 2 ; 7 * 8 = 56; resultado 5625
Se efect�a la operaci�n multiplicando la cifra de las decenas por otra mayor que �sta en una unidad, y escribiendo 25 a continuaci�n del resultado.
El m�todo se basa en lo siguiente: si el n�mero de decenas es a, todo el n�mero puede ser expresado as�:
10a + 5.
El cuadrado de este n�mero, como cuadrado de un binomio ser� igual a
100a 2 + 100a + 25 = 100a * (a + 1) + 25
La expresi�n a * (a + 1) es el resultado de multiplicar la cifra de las decenas por ella misma aumentada en urea unidad. Multiplicar el n�mero por 100 y añadirle 25 es lo mismo que colocar 25 a la derecha del producto. De este mismo m�todo se desprende el sencillo medio de elevar al cuadrado los n�meros mixtos en los que la parte fraccionaria es 1 / 2.
Por ejemplo:
(7 1 / 2) 2 = 7.5 2 = 56.25 = 56 1 / 4
(8 1 / 2) 2 = 8.5 2 = 72.25 = 72 1 / 4
Volver
2. Las cifras 1, 5 y 6
�Qui�n no ha advertido que al multiplicar por s� misma una serie de n�meros terminados en uno o cinco, el producto acaba en la misma cifra? Sin duda ser� menos conocido que lo expresado se refiere tambi�n al 6. Por esta raz�n, entre otras, la potencia de todo n�mero terminado en seis, termina asimismo en seis.
Por ejemplo:
Esta curiosa propiedad de las cifras 1, 5 y 6 puede ser fundamentada por v�a algebraica. Examin�mosla en el caso del seis.
Todo n�mero terminado en seis se descompone de esta forma:
10a + 6; 10b + 6, etc.;
donde a y b son n�meros enteros. La multiplicaci�n de dos enteros como �stos es igual a
100ab + 60b + 60a + 36 =
= 10(l0ab + 6b + 6a) + 30 + 6 =
= 10(10ab + 6b + 6a + 3) + 6
El resultado debe constar, pues, de algunas decenas y la cifra 6 en las unidades, la cual, ni que decir tiene, debe reaparecer al final.
Este mismo m�todo de demostraci�n puede ser empleado para el 1 y el 5. Lo expuesto permite afirmar que, por ejemplo,
815 723 termina en 5
491 1732 termina en 1, etc.
Volver
3. Los n�meros 25 y 76
Hay n�meros de dos cifras que tambi�n tienen la misma propiedad que las cifras 1,5 y 6: nos referimos a los n�meros 25 y - lo m�s sorprendente al 76. El producto de dos n�meros terminados en 76 acaba tambi�n en 76. Demostr�moslo. La expresi�n com�n para tales n�meros es como sigue:
100a + 76, 100b + 76, etc.
Multipliquemos dos n�meros de este tipo entre s� y obtendremos:
= 10.000ab + 7600b + 7600a + 5700 + 76 =
= 100 * (100ab + 76b + 76a + 57) + 76
El principio ha sido demostrado: el resultado terminar� en 76.
De esto se desprende que toda potencia de un n�mero acabado en 76, termina en el mismo n�mero:
Volver
4. "N�meros" infinitos
Existen tambi�n grupos de n�meros con mayor cantidad de cifras que, al figurar al final de los mismos, se conservan tambi�n en su multiplicaci�n. El n�mero de tales grupos de cifras es infinitamente grande.
Conocemos ya dos grupos compuestos de dos cifras, que poseen propiedad an�loga: el 25 y el 76. Para encontrar grupos semejantes con tres cifras hay que colocar delante del 25 o del 76 una cifra tal que nos d� un grupo de tres guarismos con la misma propiedad.
�Qu� cifra se debe colocar ante el 76? Expres�mosla con k. En este caso, el n�mero buscado de tres cifras ser�:
100k + 76
La expresi�n com�n para todo n�mero que termine en este grupo de cifras deber� ser:
1000a + 100k + 76, 1000b + 100k + 76, etc.
Multipliquemos dos n�meros de este tipo entre s� y tendremos:
+ 76.000b + 10.000k 2 + 15.200k + 5.776
Todos los sumandos, menos los dos �ltimos, terminan, por lo menos, en tres ceros. Por esto, el resultado acaba en 100k + 76 si la diferencia
= 15.000k + 5.000 + 100 (k + 7)
se divide por 1.000. Esto, evidentemente, ocurrir� cuando k sea igual a 3. As� pues, el grupo de cifras buscado es 376. A esto se debe que toda potencia de 376 termine en dicho n�mero. Por ejemplo:
376 2 = 141.376.
Si nos interesa hallar un grupo de cuatro cifras que tenga la misma propiedad, debemos colocar delante de 376 una cifra m�s. Si expresamos esta cifra con l, se nos plantear� el siguiente problema: �cu�l debe ser la cifra L para que la multiplicaci�n
(10.000a + 1000L + 376) * (10.000b + 1.000L + 376)
termine en 1.000L + 376? Si abrimos los par�ntesis de esta multiplicaci�n y prescindimos de todos los factores que terminan en cuatro ceros o m�s, nos quedar�
752.000L + 141.376
La multiplicaci�n termina con 1.000L + 376 si la diferencia
= 751.000L + 141.000 =
= (750.000L + 140 000) + 1.000 * (L + 1)
se divide por 10.000. Esto, sin duda, tendr� lugar solamente cuando L sea igual a 9.
El grupo de cuatro cifras buscado ser� 9376.
El grupo obtenido puede ser completado con una cifra m�s, para lo cual es preciso seguir id�ntico razonamiento. Obtendremos 09.376. Si damos un paso m�s hallaremos el grupo de cifras 109.376 y, despu�s, 7.109.376, etc. Una tal adici�n de cifras a la izquierda del n�mero puede ser efectuada infinita cantidad de veces. En consecuencia obtendremos un "n�mero" con infinidad de cifras:
...7 109 376.
Tales "cifras" pueden ser sumadas y multiplicadas de acuerdo con las reglas comunes: como se sabe, escr�bense de derecha a izquierda, y en este mismo sentido se suman y multiplican los n�meros "en columna"; por lo cual en la suma y en la multiplicaci�n de dos de estos n�meros se puede operar sucesivamente con todas las cifras que se quieran.
Y lo m�s interesante, por muy raro que parezca, es que ese n�mero infinito satisface a la ecuaci�n
x 2 = x
Y as� es, en efecto; el cuadrado de este "n�mero" (es decir, el resultado de multiplicarse por s� mismo) termina en 76 ya que cada uno de los factores termina en 76; por esa misma causa, el cuadrado del "n�mero" escrito acaba en 376, en 9376, etc.
Es decir, operando sucesivamente con cada una de las cifras del "n�mero" x 2 , donde x = ... 7 109 376, obtendremos las mismas cifras que ten�amos con el n�mero x, por lo cual, x 2 = x.
Hemos examinado grupos de cifras que terminan en 76. Si se aplica el mismo razonamiento para grupos de cifras terminados en 5 obtendremos los siguientes grupos de cifras:
5, 25, 625, 0625, 90625, 890 625, 2 890 625, etc.
Por ello podemos escribir otro "n�mero" infinito:
2.890.625,
que tambi�n satisface la ecuaci�n x 2 = x. Podr�amos demostrar que este "n�mero" infinito es "igual" a
(((5 2 ) 2 ) 2 ) 2 ) ...
El interesante resultado obtenido en el idioma de los "n�meros" infinitos se formula de esta manera: la ecuaci�n x 2 = x tiene (adem�s de x = 0, x = 1), otras dos ra�ces "infinitas"
x = ... 7.109.376 y x = ... 2.890.625;
sin ninguna otra soluci�n (en el sistema de base diez)
Volver
5. Compensaci�n
Antiguo problema
En tiempos remotos ocurri� el siguiente hecho. Dos mercaderes vendieron una partida de toros, recibiendo por cada animal tantos rublos como toros hab�a en la partida. Con el dinero recibido compraron un rebaño de ovejas, pagando 10 rublos por cada oveja, y un corderito. Al repartirse el rebaño en dos mitades, uno recibi� una oveja m�s, y otro, el corderillo. El que recibi� �ste fue compensado por su socio con una suma complementaria correspondiente. Siendo dicho pago complementario una cantidad entera de rublos, �de cu�ntos rublos constar�?
Soluci�n
Este problema no se presta a la traducci�n directa al "idioma algebraico", pues no puede construirse la ecuaci�n necesaria. Es preciso resolverlo mediante un procedimiento especial, el llamado razonamiento matem�tico libre. M�s tambi�n aqu� el �lgebra presta a la aritm�tica una buena ayuda. El valor en rublos de todo el rebaño es un cuadrado exacto, por cuanto dicho rebaño ha sido adquirido con el dinero recibido por la venta de n toros, a n rublos por cabeza. Uno de los socios recibi� una oveja m�s, por lo tanto, el n�mero de ovejas es impar. Tambi�n es impar, por lo mismo, el n�mero de decenas en la cantidad n 2 . �Cu�l es la cifra de las unidades? Podemos demostrar que si en un cuadrado exacto, la cifra de las decenas es impar, la de las unidades debe ser s�lo 6.
Efectivamente. El cuadrado de todo n�mero compuesto de a decenas y b unidades, es decir, (10a + b) 2 , ser� igual a
El n�mero de decenas en esta cantidad es l0a 2 + 2ab m�s algunas decenas comprendidas en b 2 . Pero 10a 2 + 2ab es divisible por dos, luego es un n�mero par. Por eso, el n�mero de decenas comprendidas en (10a + b) 2 resultar� impar s�lo cuando en el n�mero b 2 haya un n�mero impar de decenas. Recordemos lo que representa b 2 . Este n�mero es el cuadrado de la cifra de las unidades, es decir, una de las cifras siguientes:
Entre ellas, s�lo 16 y 36, tienen decenas impares, y ambos terminan en 6. Esto quiere decir que el cuadrado exacto
puede tener un n�mero impar de decenas s�lo en el caso en que termine en 6. Ahora es ya f�cil hallar la respuesta a la pregunta formulada en el problema.
Es evidente que el corderito cost� 6 rublos. El socio a quien correspondi� �ste, recibi� 4 rublos menos que el compañero. Para que el reparto sea equitativo, el poseedor del cordero debe ser compensado por su socio con 2 rublos. La compensaci�n es igual a 2 rublos.
Volver
6. Divisibilidad por 11
El �lgebra facilita en gran medida la b�squeda de indicios que permiten prever, sin recurrir a la divisi�n, si determinado n�mero es divisible por uno u otro divisor. La divisibilidad por 2, 3, 4, 5, 6, 8, 9 y 10 es ampliamente conocida. El caso del 11 es muy sencillo y pr�ctico. Supongamos que en un n�mero de varias cifras, N, la cifra de las unidades es a, la de las decenas, b; la de las centenas, c; la de las unidades de millar d, etc., es decir
donde los puntos suspensivos representan la suma de las cifras siguientes. Restemos de N el n�mero 11(b + l0c + l00d + ...), m�ltiplo de 11. La diferencia es igual a
que dar� el mismo residuo que N al dividirla por 11. Si a esta diferencia le agregamos 11 * (b + 10c + 100d + ...), m�ltiplo de 11, obtendremos
a - b - 10 * (c + 10 + ...)
que dividido por 11, da el mismo residuo que el n�mero N. Al sustraer 11 * (d + ...), m�ltiplo de 11, resultar�
que, dividido por 11 da el mismo resto que el n�mero N. De aqu� se desprende la siguiente regla de divisibilidad por 11: de la suma de las cifras que ocupan los lugares impares se resta la suma de las cifras que ocupan los lugares pares; si la diferencia es cero o m�ltiplo de 11 (negativo o positivo), el n�mero que probamos ser� m�ltiplo de 11. En caso contrario no ser� divisible por 11. Probemos, por ejemplo, el n�mero 87.635.064:
7 + 3 + 0 + 4 = 14
25 - 14 = 0
En consecuencia, el n�mero dado es divisible por 11.
Existe otro criterio de divisibilidad por 11, c�modo para n�meros relativamente pequeños. Consiste en que el n�mero que probamos se separa de derecha a izquierda en grupos de dos cifras y se suman estos grupos. Si la suma se divide por 11 sin residuo, el n�mero probado ser� m�ltiplo de 11, en caso contrario, no lo ser�. Por ejemplo, necesitamos probar el n�mero 528. Separamos el n�mero en dos grupos (5 y 28) y los sumamos:
Como 33 se divide exactamente por 11, el n�mero 528 es m�ltiplo de 11:
Demostremos este criterio de divisibilidad. Dividamos en grupos el n�mero N, que tiene varias cifras. Obtendremos grupo de dos (o de una cifra que designaremos de derecha a izquierda con a, b, c, etc., de forma que el n�mero N puede ser expresado de la forma siguiente:
Restemos de N el n�mero 99 * (b + 100c + ...), m�ltiplo de 11. El n�mero obtenido
dar�, al dividirlo por 11, el mismo residuo que el n�mero N. De este n�mero descontemos el n�mero 99 * (c + ...), m�ltiplo de 11, etc.
Por todo ello vemos que el n�mero N da el mismo resto al dividirlo por 11 que el n�mero
Volver
7. El n�mero del autom�vil
Problema
Cuando paseaban por la ciudad tres estudiantes de matem�ticas, observaron que el conductor de un autom�vil infringi� el reglamento de tr�fico. Ninguno de los estudiantes recordaba el n�mero (de cuatro cifras) de la matr�cula, pero como los tres eran matem�ticos, cada uno de ellos advirti� alguna particularidad de dicho n�mero. Uno de ellos advirti� que las dos primeras cifras eran iguales. El segundo se dio cuenta de que tambi�n coincid�an las dos �ltimas cifras. Y, por �ltimo, el tercero aseguraba que todo el n�mero de cuatro cifras era un cuadrado exacto. �Puede determinarse el n�mero de la matr�cula del autom�vil vali�ndose tan s�lo de estos datos?
Soluci�n
Expresemos la primera y la segunda cifra del n�mero buscado con la a, y la tercera y la cuarta con la b. Entonces el n�mero ser� igual a
Este n�mero es divisible por 11 y, por eso, (siendo un cuadrado exacto) se divide tambi�n por 11 2 . Con otras palabras, el n�mero 100a + b se divide por 11. Al emplear cualquier de los criterios de divisibilidad expuestos, deduciremos que el n�mero a + b es divisible por 11. Pero esto significa que
por cuanto cada una de las cifras a, b es menor que diez.
La �ltima cifra b que es un cuadrado exacto, puede tomar los siguientes valores:
Por eso, para la cifra a, que es igual a 11 - b, se encuentran los siguientes valores posibles:
Los dos primeros valores son inaceptables, quedando, pues, los siguientes:
| b = 4 | a = 7 |
| b = 5 | a = 6 |
| b = 6 | a = 5 |
| b = 9 | a = 2 |
Vemos, en consecuencia, que el n�mero de la matr�cula debe ser alguno de �stos:
Pero como los tres �ltimos no son cuadrados - el n�mero 6655 es divisible por 5, pero no por 25; el 5566 se divide por 2, pero no por 4, y 2299 (producto de 12 * 19) tampoco es cuadrado - no queda m�s que 7744, segunda potencia de 88, que nos ofrece la soluci�n del problema.
Volver
8. Divisibilidad por 19
Ocup�monos del siguiente criterio de divisibilidad por 19.
Un n�mero es m�ltiplo de 19 s�lo en el caso en que sus decenas m�s el doble de sus unidades forme un m�ltiplo de 19.
Soluci�n
Todo n�mero N puede ser presentado como
donde x es el n�mero de decenas (no la cifra que ocupa las decenas, sino la cantidad de decenas del n�mero); y es la cifra de las unidades. Tenemos que demostrar que N es m�ltiplo de 19 tan s�lo cuando
es m�ltiplo de 19. Para esto multipliquemos N' por 10, y del producto restemos N de donde
Con esto se demuestra que si N' es m�ltiplo de 19, entonces
y se dividir� exactamente por 19 y al contrario, si N se divide por 19, entonces
ser� m�ltiplo de 19, y en ese caso tambi�n N' ser� m�ltiplo de 19. Supongamos que se precisa saber si el n�mero 47.045.881 se divide por 19. Apliquemos sucesivamente nuestro criterio de divisibilidad
|
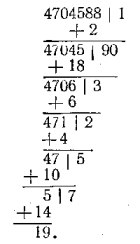
Como 19 se divide exactamente por 19, los n�meros 57, 475, 4.712, 47.063, 470.459, 4.704.590, 47.045.881 son m�ltiplos de 19. Por lo tanto, tambi�n se divide el n�mero propuesto por 19.
Volver
9. Teorema de Sof�a Germain
He aqu� un problema propuesto por Sof�a Germain, conocida matem�tica francesa: Demu�strese que los n�meros del tipo a 4 + 4 son compuestos, (con la condici�n de que a no sea igual a 1).
Soluci�n
La demostraci�n se desprende de las siguientes transformaciones:
a 4 + 4 = a 4 + 4a 2 + 4 - 4a 2 = (a 2 + 2) 2 - 4a 2 =
= (a 2 + 2) 2 - (2a) 2 = (a 2 + 2 - 2a) * (a 2 + 2 + 2a)
De aqu� se desprende que, el n�mero a 4 + 4 puede ser expresado en forma de dos factores que no sean iguales a �l ni a la unidad, es decir, es un n�mero compuesto.
Volver
10. N�meros compuestos
Los n�meros primos, es decir, aquellos que son mayores que 1 y no se dividen exactamente m�s que por s� mismo y la unidad, son infinitos.
A partir de 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 ..., su serie es interminable. Intercalados entre los n�meros compuestos, dividen la serie de n�meros naturales en series m�s o menos prolongadas de n�meros compuestos.
�Cu�l es la continuidad de estas series? �Puede encontrarse alguna que abarque, por ejemplo, hasta mil n�meros compuestos sucesivos?
Puede demostrarse, aunque parezca inveros�mil, que las series de n�meros compuestos, situadas entre los primos, pueden ser de cualquier extensi�n. No hay l�mites para la prolongaci�n de tales grupos, ya que pueden estar formados por miles, millones, trillones, etc., de n�meros compuestos.
Para mayor facilidad no serviremos del signo convencional n!, que representar� el producto de todos los n�meros consecutivos, del 1 a n inclusive. Por ejemplo, 5! = 1 * 2 * 3 * 4 * 5. Demostremos como la serie
...hasta [(n + 1)! + n + 1] inclusive
est� formada por n n�meros compuestos consecutivos.
Estos n�meros van sucedi�ndose uno tras otro en serie natural, por cuanto cada uno es superior en una unidad al que le antecede. Queda tan solo por demostrar que todos ellos son compuestos.
El primero
[(n + l)! + 2] = 1 * 2 * 3 * 4 * 5 * 6 * 7 * ... * [(n + l) + 2],
es par, ya que en sus dos sumandos contiene el factor 2. Y todo n�mero par mayor que 2 es compuesto.
El segundo
consta de dos sumandos, cada uno de los cuales es m�ltiplo de 3. Por lo tanto, este n�mero tambi�n es compuesto.
El tercero
es divisible por 4, ya que se compone de sumandos m�ltiplos de 4. De manera an�loga establecemos que el n�mero
es m�ltiplo de 5, etc. En otras palabras, cada uno de estos n�meros contiene un factor, adem�s del mismo n�mero y de la unidad, por lo tanto ser� compuesto. Si se desea obtener 5 n�meros compuestos consecutivos basta sustituir la n por el 5 en la serie anterior. De este modo resultar�
Por �sta no es la �nica serie de cinco n�meros compuestos consecutivos. Existen tambi�n, como por ejemplo:
O n�meros todav�a menores:
Intentemos resolver ahora un problema: Escribir diez n�meros compuestos consecutivos.
Soluci�n
En virtud de lo expuesto, el primero de los diez n�meros buscados puede ser
Por consiguiente, para la serie de n�meros buscada, nos sirve
Sin embargo, existen series de diez n�meros compuestos consecutivos considerablemente m�s pequeños. Incluso puede señalarse una serie no de diez, sino de trece n�meros, comprendidos entre la primera y la segunda centena:
Volver
11. Acerca de los n�meros primos
El hecho de que existan infinitas series muy prolongadas de n�meros compuestos consecutivos puede inducir a la creencia de que las series de n�meros primos son limitadas. Por ello, no ser� de m�s demostrar que la cantidad de dichas series de n�meros primos es infinita.
Esta demostraci�n se debe al matem�tico Euclides, de la antigua Grecia, figura en sus c�lebres Principios. Pertenece a la categor�a de demostraciones por reducci�n al absurdo. Supongamos que la serie de n�meros primos es limitada y que representamos con la N el �ltimo n�mero de ella. Desarrollemos la factorial de N:
Al sumarle la unidad, resultar� N! + 1
Este n�mero, al ser entero, debe contener por lo menos un factor primo, es decir, debe ser divisible, aunque no sea m�s que por un n�mero primo. Pero todos los n�meros primos, de acuerdo con el supuesto no superan el n�mero N; mientras que el n�mero N! + 1 no es m�ltiplo de ninguno de los n�meros menores o iguales a N, pues su divisi�n siempre da un resto equivalente a la unidad.
Por lo tanto, no puede aceptarse que la serie de n�meros primos sea limitada: tal suposici�n conduce al absurdo. Por consiguiente, por muy considerable que sea el grupo de n�meros consecutivos compuestos que nos encontremos en la serie de n�meros naturales, puede tenerse la seguridad de que al remontarse por ella se encontrar�n infinitos n�meros primos.
Volver
12. El mayor n�mero primo conocido
Una cosa es estar convencido de que existen n�meros primos tan grandes como se quiera, y otra saber cu�les son esos n�meros. Cuanto mayor sea el n�mero natural, tanto m�s operaciones hay que realizar para conocer si es primo o no. He aqu� el n�mero primo m�s grande de cuantos se conocen:
Este n�mero tiene cerca de setecientas cifras del sistema decimal. Los c�lculos que sirvieron para demostrar que este n�mero es primo fueron realizados en las m�quinas modernas de calcular. (V�anse los cap�tulos I y II).
Volver
13. Un c�lculo muy laborioso
En la pr�ctica del c�lculo se encuentran operaciones matem�ticas cuya realizaci�n ser�a extraordinariamente dif�cil si para ello no se aplicaran los m�todos simplificadores del �lgebra. Supongamos que sea necesario efectuar las siguientes operaciones:
(Este c�lculo es necesario para establecer si la t�cnica relacionada con las velocidades de los movimientos de los cuerpos - pequeñas en comparaci�n con la velocidad de la difusi�n de las ondas electromagn�ticas - puede valerse de las antiguas leyes que regulan la suma de velocidades, sin tener en cuenta aquellos cambios que la teor�a de la relatividad ha introducido en la mec�nica. De acuerdo con la mec�nica antigua, el cuerpo sometido a dos movimientos, efectuados en una misma direcci�n, con velocidades de v 1 y v 2 kil�metros por segundo, tiene una velocidad de (v l + v 2 ) kil�metros por segundo. La nueva teor�a aplica la siguiente f�rmula para la velocidad de los cuerpos, en kil�metros por segundo,
donde c es la velocidad de difusi�n de la luz en el vac�o, aproximadamente igual a 300 000 kil�metros por segundo. Un cuerpo sometido a dos movimientos, efectuados en una misma direcci�n, y a una velocidad de kil�metro por segundo cada uno, seg�n la antigua mec�nica desarrollaba 2 kil�metros por segundo de velocidad y, seg�n la nueva, en kil�metros por segundo,
�Cu�l es la diferencia entre esas dos f�rmulas? �Es perceptible esa diferencia para los aparatos m�s sensibles de medici�n? A fin de aclarar esta importante cuesti�n es preciso realizar el c�lculo indicado).
Empleemos dos m�todos: primero, el aritm�tico, y despu�s, mostremos c�mo se puede efectuar mediante el �lgebra. Basta con echar un vistazo a la larga serie de cifras que figuran m�s abajo para convencerse de la indiscutible superioridad del procedimiento algebraico.
En primer lugar transformemos el quebrado
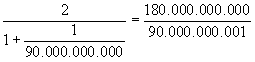
Efectuamos ahora la divisi�n del numerador por el denominador:
 |
Esta operaci�n resulta agotadora y laboriosa, siendo muy f�cil confundirse e incurrir en error, en tanto que para la soluci�n del problema tiene mucha importancia saber con exactitud d�nde termina el per�odo del nueve y comienza el de otra cifra.
Comp�rese ahora con qu� brevedad cumple su tarea el �lgebra, vali�ndose del siguiente planteamiento: si a es un quebrado muy pequeño, entonces
donde el signo » significa "aproximadamente igual".
Es muy f�cil convencerse de la veracidad de este aserto: comparemos el dividendo 1 con el producto del divisor por el cociente:
es decir,
Como a es una fracci�n muy pequeña (por ejemplo 0,001), el valor de a 2 ser� todav�a inferior (0,000001), pudiendo ser despreciado.
Apliquemos lo expuesto a nuestro c�lculo:
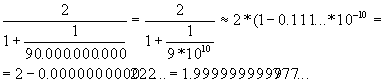
Se llega, pues, al mismo resultado, pero el procedimiento es mucho m�s corto.
(Quiz�s tenga inter�s el lector en conocer la importancia que reviste el resultado del problema. Por �l se deduce que en virtud de la escasa magnitud de las velocidades examinadas - en comparaci�n con la de la luz - , no se observa en la pr�ctica ninguna desviaci�n de la antigua ley de la suma de velocidades: esa desviaci�n se pone de manifiesto s�lo en la cifra und�cima del n�mero hallado, en tanto que las mediciones de longitud m�s exactas no rebasan la novena cifra, y en la pr�ctica, la t�cnica se limita a 4 o 6 cifras. En consecuencia, podemos afirmar sin ninguna reserva que la nueva mec�nica, la de Einstein, no altera los c�lculos t�cnicos relativos al movimiento "lento" de los cuerpos en el espacio (en comparaci�n con la velocidad de difusi�n lum�nica).
Pero existe una rama de la vida actual, donde esta conclusi�n incondicional hace falta tomarla con cuidado. Se trata de la cosmon�utica. Ahora hemos alcanzado ya las velocidades de 10 km por segundo (durante los vuelos de sputniks y cohetes). En este caso la divergencia de la mec�nica cl�sica y de la de Einstein se pone de manifiesto ya en la cifra novena. Hay que tener en cuenta qu� velocidades mayores no est�n tan lejos.
14. En ocasiones es preferible no recurrir al �lgebra
Junto a los casos en los que el �lgebra presta un gran servicio a la aritm�tica, hay otros en que su aplicaci�n da lugar a complicaciones innecesarias. El verdadero conocimiento de las matem�ticas consiste en saber emplear los recursos matem�ticos de tal suerte que sirvan para encontrar el camino m�s corto y seguro, sin reparar en que el m�todo de soluci�n pertenezca a la aritm�tica, al �lgebra, a la geometr�a, etc. Por eso ser� �til examinar un caso en que el empleo del �lgebra tan solo embaraza la soluci�n. Como ejemplo aleccionador puede servirnos el siguiente problema:
Encontrar el n�mero m�s pequeño entre los que divididos
| por | 2 | dan de residuo | 1 |
| por | 3 | dan de residuo | 2 |
| por | 4 | dan de residuo | 3 |
| por | 5 | dan de residuo | 4 |
| por | 6 | dan de residuo | 5 |
| por | 7 | dan de residuo | 6 |
| por | 8 | dan de residuo | 7 |
| por | 9 | dan de residuo | 8 |
Soluci�n
Propusi�ronme este problema acompañ�ndolo con las siguientes palabras: "�C�mo lo resolver�a usted? Aqu� hay demasiadas ecuaciones y resulta muy lioso"
La cosa es sencilla. Para la soluci�n del problema no hacen falta ni ecuaciones ni �lgebra. Se resuelve con un sencillo razonamiento aritm�tico.
Agreguemos una unidad al n�mero buscado. �Cu�l ser� el residuo de este n�mero si lo dividimos por dos? Ser� 1 + 1 = 2; es decir, el n�mero se divide por 2 sin residuo. De esta misma manera se divide sin residuo por 3, 4, 5, 6, 7, 8 y 9. El menor de estos n�meros ser� 9 * 8 * 7 * 5 = 2.520, y el n�mero buscado, 2.519, lo que es f�cil comprobar.
Volver
|
|
|