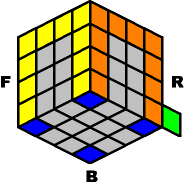

All 8 bottom edges are in the bottom layer, and chances are they are pretty much scrambled. The first step is to arrange them in the correct positions. Randomly choose a front side, and proceed to solve the back edges; starting with the back-left edge first and the back-right second.
Note: these diagrams look strange. The first one appears to take 4 edges and cram them into one. What the first diagram actually means is that if an edge cube is coming from ANY edge-side, then you must repeat the sequence until it appears in the back-left edge. You may have to repeat this sequence four times before that happens.
The second diagram represents any edge from the front moving to the back-left edge. You may have to repeat that squence twice before it lands there. The dark squares on both diagrams are edges cubes that do not move at all during the process.
Now continue to...
~~~ Move an edge to the back-left ~~~ |
||||
| ______________________________ | ||||
Move an edge
|
Repeat the |
...until the edge lands
|
||
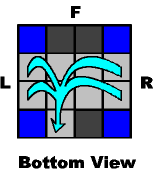 |
M- B- M+ B2
|
You may have to |
||
| ______________________________ | ||||
Move an edge
|
Repeat the |
...until the edge lands
|
||
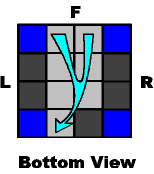 |
M- B2 M+ B- |
You may have to |
||
~~~ Move an edge to the back-right: ~~~ |
||||
| ______________________________ | ||||
Move an edge
|
Repeat the |
...until the edge lands
|
||
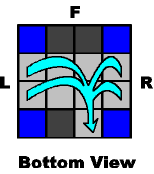 |
N- B+ N+ B2
|
You may have to |
||
| ______________________________ | ||||
Move an edge
|
Repeat the |
...until the edge lands
|
||
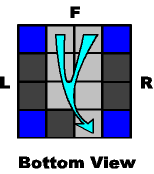 |
N- B2 N+ B+ |
You may have to |
||
If you are lucky, the edges going to the back are already paired. You can still move them one at a time, or you can use these shortcuts:
~~~ Move an edge-pair ~~~ |
||||
...from the left: |
...from the front: |
...from the right: |
||
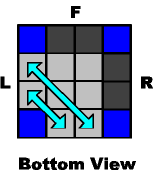 |
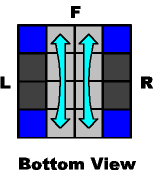 |
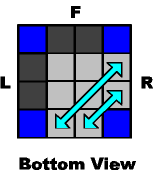 |
||
N- B+ N+ B2 |
M- M- B2 |
M- B- M+ B2 |
||
All sequences only have to be performed once to accomplish the move.
Both back edges
|
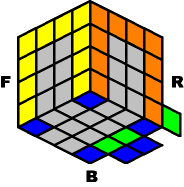 |
...rotate the entire
|
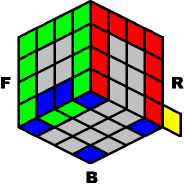 |
...and solve the
|
Once again, you have to use the same sequences as before, except this time, the edges are coming from the sides only.
Move a single
|
Move a single
|
Swap the left
|
Swap the right
|
|||
 |
 |
 |
 |
|||
M- B- M+ B2 |
N- B+ N+ B2 |
N- B+ N+ B2
|
M- B- M+ B2
|
The back and
|
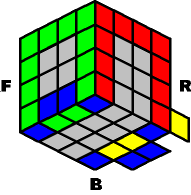 |
...rotate the entire
|
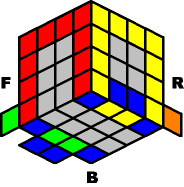 |
...and solve the
|
This time, you only have to use the sequences that move the edges from the front to the back:
Move a single
|
Move a single
|
Swap the front
|
|||
 |
 |
 |
|||
M- B2 M+ B-
|
N- B2 N+ B+
|
M- M- B2 |
Once you solve the back side (for the third time), the remaining 2 edge cubes are forced in the front side, where they belong! Therefore, all 8 bottom edges are in place. Now for the next step: inverting.
There are 5 different inversion schemes:
For each inversion scheme, you must rotate the entire puzzle so that the inverted pairs are positioned exactly like the ones in the diagrams, before attempting the sequence of moves!
~~~ Case #1: Invert two adjacent edge-pairs ~~~ |
||||
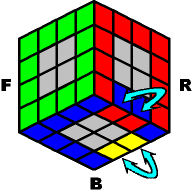 |
[MN]- B- [MN]+ B- |
Result: | ||
| ________________________________________ | ||||
~~~ Case #2: Invert two opposite edge-pairs ~~~ |
||||
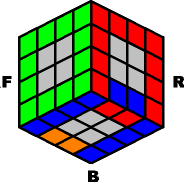 |
[MN]- B- [MN]+ B- |
Result: |
||
| ________________________________________ | ||||
~~~ Case #3: Invert four edge-pairs ~~~ |
||||
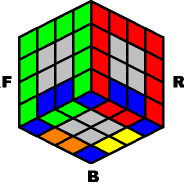 |
[MN]- B- [MN]+ B- |
Result: |
||
| ________________________________________ | ||||
~~~ Case #4: Invert three edge-pairs ~~~ |
||||
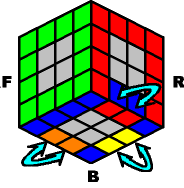 |
M- B- M- B2 |
Result: |
||
| ________________________________________ | ||||
~~~ Case #5: Invert one edge-pair ~~~ |
||||
 |
M- B- M- B2 |
Result: |
||
As it turns out, only two different sequences were used throughout all five cases. Now that the bottom edges are solved, the only thing left are the Middle Centers.