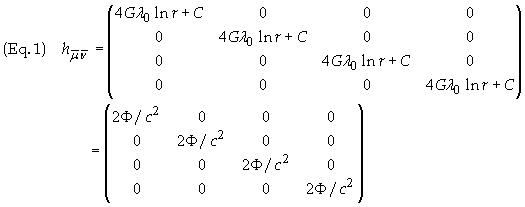
Gravitational
Field of a
Long Moving Rod
Back
to Physics World
Back
to General Relativity
Problem: Consider an infinitely long thin rod, with linear proper mass density l0, which lays at rest on the x-axis in frame S0. Neglect all stresses in the rod. In frame S, which is moving in the +x direction with speed v, the rod is moving in the -x direction with speed v. Define r0 such the Newtonian potential vanishes at r0, i.e. F (r0) = 0. Using the weak field limit
(a) Find the gravitational
field, gmn,
in S by transforming from S0
to S using a background Lorentz transformation.
(b) Find duz /dt for u = 0, r
= r0,
and y = 0 where uz º
dz/dt for a particle in free-fall.
(c) Find dPz
/dt for u º
|u| (relativistic speed) = speed of particle. Let and z
= r0
for a particle in free-fall.
Solution
(a): It can be shown that the gravitational
field in S0
is given by
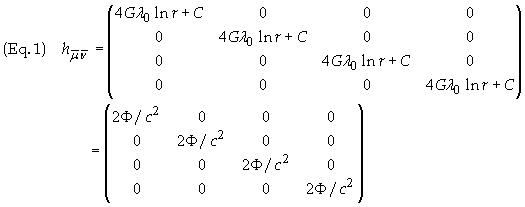
where C is an
arbitrary constant and F
= c2h0/2.
Since the field is weak we employ a background
Lorentz transformation , which is a transformation of the form
![]()
where
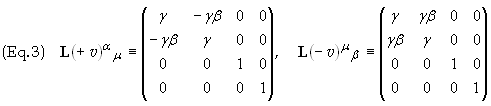
The transformation on the
left is a boost in the +x direction with speed v. The
transformation on the right is the inverse transformation. Transform the
gravitational field using Eq. (2). The non-vanishing components are h00, h01,
h11, h22
and h33. Noting that r = r (y, z)
remains unchanged since y and z remain unchanged and therefore
so does F.
We find the components of the field in the new frame
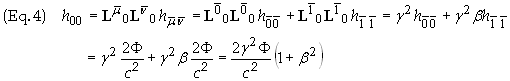
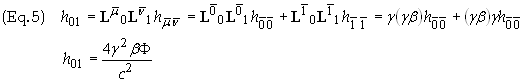
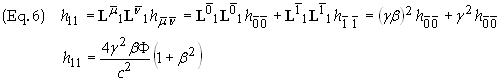
![]()
![]()
Summary:
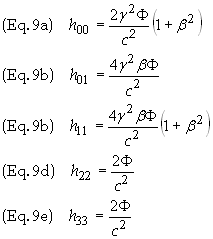
The metric in S then
becomes
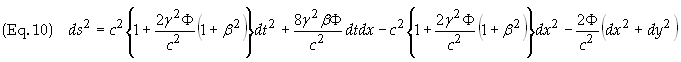
Solution
(b): The acceleration in the weak field limit
is given by
![]()
At r = r0 = z, y = 0, for u = 0, dt/dt = 1. U3 = -uz and U0 = c. Eq. (11) then becomes
![]()
The derivative in Eq. (12)
is then (Note: y = 0 Þ
r = z = r0)
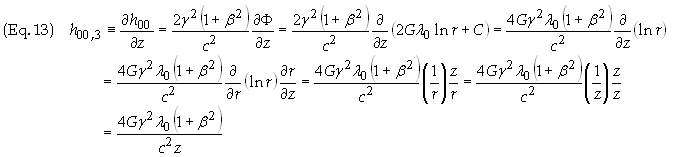
l = g2l0 is the linear mass density as measured in S. Eq. (12), with z = r0 then becomes
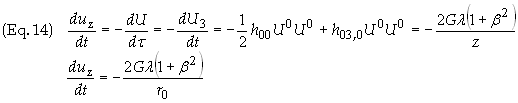
Solution
(c): Multiply Eq. (11) through by the proper mass, m0,
to give
![]()
Set m = 3 to find dpx/dt
for a particle in free-fall, with z = r0,
becomes
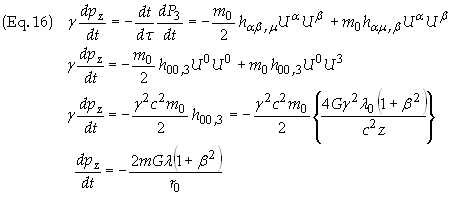
Back to
General Relativity
Back to Physics World