Gravitational Field of an
Infinitely Long Rod

Back to Physics World
Back to General Relativity

Problem: Consider an infinitely long thin rod that is at rest in frame S on the x-axis. Define r₀ such that gravitational potential F is zero at that distance from the rod. I.e. F(r0) = 0.

(a) Find the gravitational field, g_mn, in S by explicitly solving Einstein’s weak field equations.
(b) Find du_z /dt for u = 0, r = r₀, and y = 0 where u_z º dz/dt for a particle in free-fall. Consider the results only in the z plane, i.e. let y = 0. Then r = z.
(c) Find dp_z /dt for u º |u| (relativistic speed), r = r₀, and y = 0 for a particle in free-fall.

Solution (a): Let the linear proper mass density (mass per unit length) of the rod in S be l₀. The Newtonian gravitational potential of the rod for y = 0 is given by

C is a constant of integration. This result may be obtained from the weak field limit of Einstein equations and gauge condition, i.e. respectively

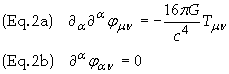
Since all matter in the S frame is motionless then we expect the gravitational field to be time independent. Therefore since the energy-momentum tensor vanishes outside the rod we obtain from Eq. (2a)

where f_mn are defined as

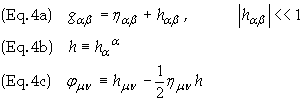
In cylindrical coordinates

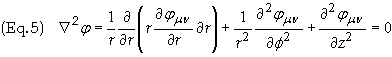
Due to rotational symmetry the f_mn will be a function of r only. Thus

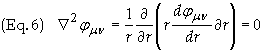
Therefore the term inside the parentheses is constant. Let these constants be C_mn. Then

The solution is obtained directly from integration to obtain

The gauge condition from Eq. (2b) becomes

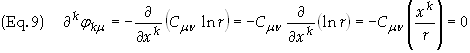
Eq. (8) must be valid for all values of xk which can only be true if C_mn = 0. The only non-vanishing value must be C₀₀. Therefore only

does not vanish. Thus we arrive at Eq. (1). To determine C₀₀ recall

where

Thus the 00 component of Eq. (10) becomes

h₀₀ is related to the Newtonian potential as

Comparing Eq. (1), (12) and Eq. (13) shows that

We then have from Eq. (9)

The other components of h00 are found from Eq. (10)

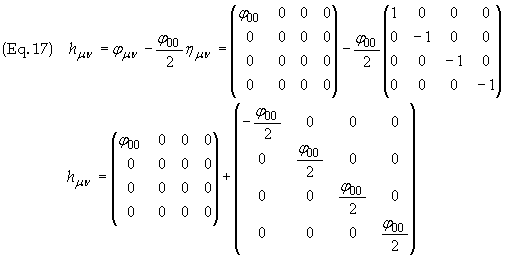
Upon substitution of Eq. (16) we can simplify Eq. (17) to

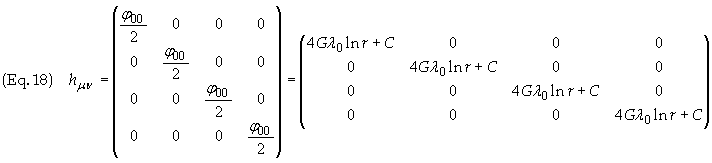
The metric tensor g_mn is related to h_mn by

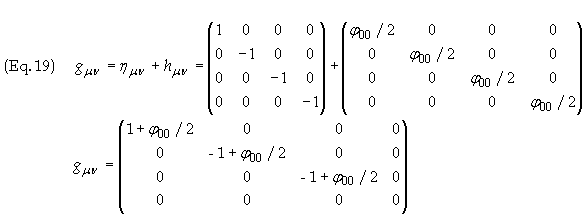
Therefore we find the final expression for the field by substituting Eq. (16) into Eq. (19) to obtain the result

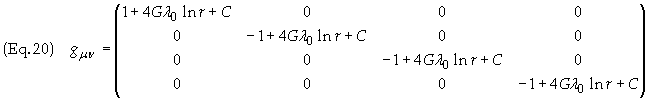
C is chosen such that F(r0) and therefore g₀₀(r₀) = 1. I.e. C º -4Gl₀ln r₀. Thus the coordinate clock is located at r = r₀

Solution (b): By assumption U¹ = U² = U³ = 0, r = r₀, and y = 0. It can be shown that

At r = r₀, z = 0, for u = 0 dt/dt = 1. U³ = -u_z and U₀ = c. Eq. (19) then becomes

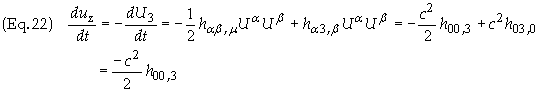
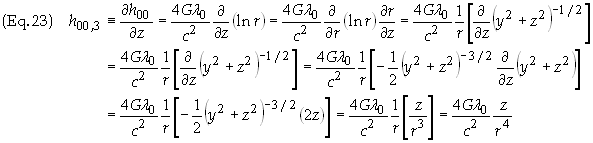
Warning: Eq. (23) may not appear to be correct. When this page was originally posted the result obtained was h00,3 = 4Gl0/c2z. This will be the value used from herein. The problem will be corrected at a later date.

The last part follows due to the fact that y = 0 and therefore r = z. The final result is therefore

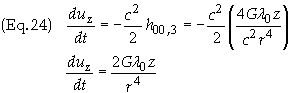
Solution (c): By assumption u is relativistic, r = r₀, and y = 0. At r = z = 0, for u relativistic and in the weak field limit

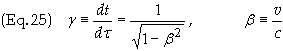
To find dp_z/dt note that U₀ = cg and p_z = P³ = -P³. Eq. (21) then becomes upon multiplying through by the proper mass m₀ to obtain

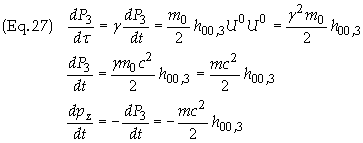
Recall the value of h₀₀ found in Eq. (18), i.e. h₀₀ = 4Gl₀ln z. The result h₀₀,₃ was calculated above in Eq. (23) giving h_00,3 = 4Gl₀/c²z. The last part follows due to the fact that y = 0 and therefore r = z. The final result is therefore

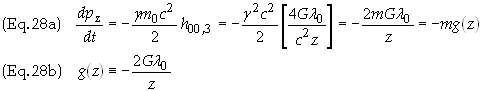
m = gm₀ is the mass of the particle whose proper mass is m₀.

Back to General Relativity
Back to Physics World