Weak Field Limit 

Back to Physics World
Back to General Relativity

The weak field limit of Einstein’s field equations produces the linearized field equations. The weak field is defined by

That is to say that the metric tensor is written in terms of the sum of the Minkowski metric and correction term whose components are much less than unity. In terms of this metric the Christoffel symbols become

Eq. (2) introduces the convention where, in the weak field limit, indices are raised and lowered using, hab and hab rather gab and gab respectively Expanding Eq. (2) gives

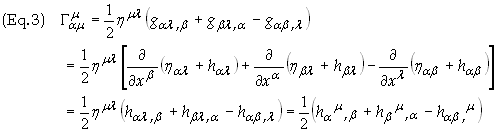
The Riemann tensor is

Since the Christoffel symbols are first order quantities, the only contribution to the Riemann tensor will come from the derivatives of G, not the G² terms. Therefore in the weak field limit the Riemann tensor becomes

Or upon lowering a we obtain

The Christoffel symbols in Eq. (6) are

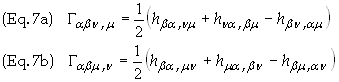
Subtracting Eq. (7b) from Eq. (7a) gives the Riemann tensor

Raise the a index to obtain

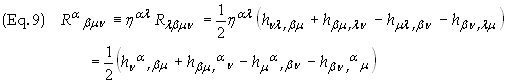
Contract the Riemann tensor over m to obtain the Ricci tensor

Substitute

into Eq. (10) and relabel the indices to obtain

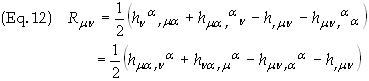
Raise the m index to obtain

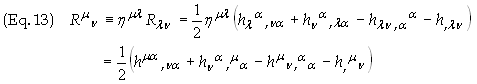
Contract the Ricci tensor over m to obtain the Ricci scalar

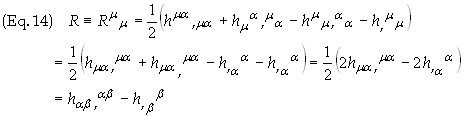
Einstein’s field equation is

Substituting Eq. (12) and Eq. (14) as well as h_ab @ g_ab into Eq. (15) yields after multiplying through by 2

It can be shown that Eq. (16) is invariant under the gauge transformation

Gauge invariance implies that the field equations do not determine the field uniquely. One may then eliminate some ambiguity in the solution by imposing the gauge condition

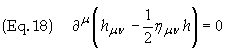
This is known as the Hilbert condition. The field equations then reduce to

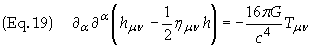
This expression may be made much simpler by defining the following quantity

The field equation then becomes

The gauge condition then becomes

It can be shown that the quantity g₀₀ is related to the Newtonian potential F as

Therefore since g₀₀ = 1 + h₀₀ we find

To find the equation of motion use the Lagrange’s equations

where

The Lagrangian is given by

Calculate the covariant components of the 4-momentum P

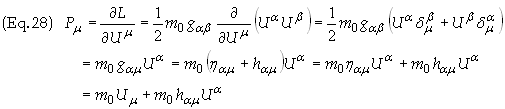
The right side of Eq. (25) is

The equation of motion is then

The left side equals

The second term on the right side is a product of the acceleration, which is of order h, and terms of order h and is thus of order h². It may therefore be dropped to give

Eq. (30) then becomes

The solution to Eq. (21) is

Back to General Relativity
Back to Physics World