An Overview
Artificial Intelligence (AI) is the area of computer science focusing on creating machines that can engage on behaviors that humans consider intelligent. The ability to create intelligent machines has intrigued humans since ancient times, and today with the advent of the computer and 50 years of research into AI programming techniques, the dream of smart machines is becoming a reality. Researchers are creating systems which can mimic human thought, understand speech, beat the best human chessplayer, and countless other feats never before possible. Find out how the military is applying AI logic to its hi-tech systems, and how in the near future Artificial Intelligence may impact our lives.

	Artificial Neural Networks
	Also referred to as connectionist architectures, parallel distributed processing, and neuromorphic systems, an artificial neural network (ANN) is an information-processing paradigm inspired by the way the densely interconnected, parallel structure of the mammalian brain processes information. Artificial neural networks are collections of mathematical models that emulate some of the observed properties of biological nervous systems and draw on the analogies of adaptive biological learning. The key element of the ANN paradigm is the novel structure of the information processing system. It is composed of a large number of highly interconnected processing elements that are analogous to neurons and are tied together with weighted connections that are analogous to synapses.
	Learning in biological systems involves adjustments to the synaptic connections that exist between the neurons. This is true of ANNs as well. Learning typically occurs by example through training, or exposure to a truthed set of input/output data where the training algorithm iteratively adjusts the connection weights (synapses). These connection weights store the knowledge necessary to solve specific problems.
	Although ANNs have been around since the late 1950's, it wasn't until the mid-1980's that algorithms became sophisticated enough for general applications. Today ANNs are being applied to an increasing number of real- world problems of considerable complexity. They are good pattern recognition engines and robust classifiers, with the ability to generalize in making decisions about imprecise input data. They offer ideal solutions to a variety of classification problems such as speech, character and signal recognition, as well as functional prediction and system modeling where the physical processes are not understood or are highly complex. ANNs may also be applied to control problems, where the input variables are measurements used to drive an output actuator, and the network learns the control function. The advantage of ANNs lies in their resilience against distortions in the input data and their capability of learning. They are often good at solving problems that are too complex for conventional technologies (e.g., problems that do not have an algorithmic solution or for which an algorithmic solution is too complex to be found) and are often well suited to problems that people are good at solving, but for which traditional methods are not.
	There are multitudes of different types of ANNs. Some of the more popular include the multilayer perceptron which is generally trained with the backpropagation of error algorithm, learning vector quantization, radial basis function, Hopfield, and Kohonen, to name a few. Some ANNs are classified as feedforward while others are recurrent (i.e., implement feedback) depending on how data is processed through the network. Another way of classifying ANN types is by their method of learning (or training), as some ANNs employ supervised training while others are referred to as unsupervised or self-organizing. Supervised training is analogous to a student guided by an instructor. Unsupervised algorithms essentially perform clustering of the data into similar groups based on the measured attributes or features serving as inputs to the algorithms. This is analogous to a student who derives the lesson totally on his or her own. ANNs can be implemented in software or in specialized hardware.
	Artificial Neural Networks Applications
	Classification
	Business
	· Credit rating and risk assessment,  Insurance risk evaluation, Fraud detection
	· Insider dealing detection, Marketing analysis, Mailshot profiling
	· Signature verification, Inventory control
	Engineering
	· Machinery defect diagnosis, Signal processing, Character recognition
	· Process supervision, Process fault analysis, Speech recognition
	· Machine vision,   Speech recognition,  Radar signal classification
	Security
	· Face recognition, Speaker verification, Fingerprint analysis
	Medicine
	· General diagnosis, Detection of heart defects
	Science
	· Recognising genes, Botanical classification, Bacteria identification
	· Modelling
	Business
	· Prediction of share and commodity prices, .Prediction of economic indicators
	Engineering
	· Transducer linearisation, Colour discrimination, Robot control and navigation
	· Process control, Aircraft landing control, Car active suspension control
	· Printed Circuit auto routing, Integrated circuit layout, Image compression
	Science
	· Prediction of the performance of drugs from the molecular structure.
	· Weather prediction, Sunspot prediction
	Medicine
	· Medical imaging and image processing
	Forecasting
	- Future Sales, Production Requirements,  Market Performance
	- Economic Indicators, Energy Requirements,  Time Based Variables.
	Novelty Detection
	- Fault Monitoring, Performance Monitoring,  Fraud Detection,
	- Detecting Rare Features
	- Different Cases.
	Who needs Artificial Neural Networks?
	People who have to work with or analyse data in any form. People who in business, finance, or industry and whose problems are either complex , laborious, 'fuzzy' or simply un-resolvable with present methods. People who simply want to improve on their current techniques and gain competitive advantage.
	Why are they the best method for data analysis?
	Neural networks outperform current methods of analysis because they can successfully
	Deal with the non-linearities of the world we live in
	Be developed from data without an initial system model
	Handle noisy or irregular data from the real world
	Quickly provide answers to complex issues
	Be easily and quickly updated
	Interpret information from tens or even hundreds of variables or parameters
	Readily provide generalised solutions
	What are the main types of neural network learning ?
	There exist two primary types of neural network learning: supervised and unsupervised .
	Supervised Learning
	Supervised learning is a process of training a neural network by giving it examples of the task we want it to learn. I.e., learning with a teacher. The way this is done is by providing a set of pairs of vectors (patterns), where the first pattern of each pair is an example of an input pattern that the network might have to process and the second pattern is the output pattern that the network should produce for that input which is known as a target output pattern for whatever input pattern. This technique is mostly applied to feed forward type of neural networks.
	For more detailed information click here on supervised learning
	Unsupervised Learning
	Unsupervised learning is a process when the network is able to discover statistical regularities in its input space and automatically develops different modes of behaviour to represent different classes of inputs (in practical applications some 'labelling' is required after training, since it is not known at the outset which mode of behaviour will be associated with a given input class). Kohonen's self-organising (topographic) map neural networks use this type of learning.
	We have to bear in mind that neural networks learning process is about changing the state of connectivities. Some algorithms (most of them) involve changing the weights of the connections. However, other ones involve adding and retrieving connections as well as changing their weights values.
	For more detailed information click here on unsupervised learning
	Artificial Neural Networks Resources
PDP	The PDP simulator package comes with McClelland and Rumelhart's book"Explorations in Parallel Distributed Processing" PC and UNIX platform. The latest version is available from ftp.nic.funet.fi.
Neuro Solutions	A neural network simulator which combines a graphical design interface with advanced learning procedures, such as recurrent backpropagation and backpropagation through time. Notable features include C++ code generation, user-defined algorithms and integration with Excel. Free evaluation copy available for download. Windows 95/98/NT platform www.nd.com/download.htm www.nd.com/products/nsv3.htm
Mactivation	A Neural network simulation system. Macintosh platform The latest version is available from ftp.cs.colorado.
NeurDS	Supports various type of networks. DEC systems. The latest version is available from ftp.gatekeeper.dec.com
Rochester Connectionist  Simulator	A simulator program for arbitrary types of neural nets. Comes with a backprop package and a X11/Sunview interface. Sun platform The latest version is available from ftp.cs.rochester.edu. Additional information is available from ftp.cs.rochester.edu.
Xerion	This package includes simulations of backpropagation, Boltzmann Machine and Kohonen Networks. SUN platform The latest version is available from ftp.cs.toronto.edu. Additional information is available from ftp.cs.toronto.edu.
Attrasoft	A lot of ANN applications including Stock Prediction, Business Decision, Medical Decision. http://attrasoft.com/
AI  Information Bank	This page is part of the AI Information Bank / AI Intelligence Web site. http://aiintelligence.com/aii-info/techs/nn.htm

Fuzzy Logic
Fuzzy Logic is a form of logic used in some expert systems and other artificial-intelligence applications in which variables can have degrees of truthfulness or falsehood represented by a range of values between 1 (true) and 0 (false). With fuzzy logic, the outcome of an operation can be expressed as a probability rather than as a certainty. 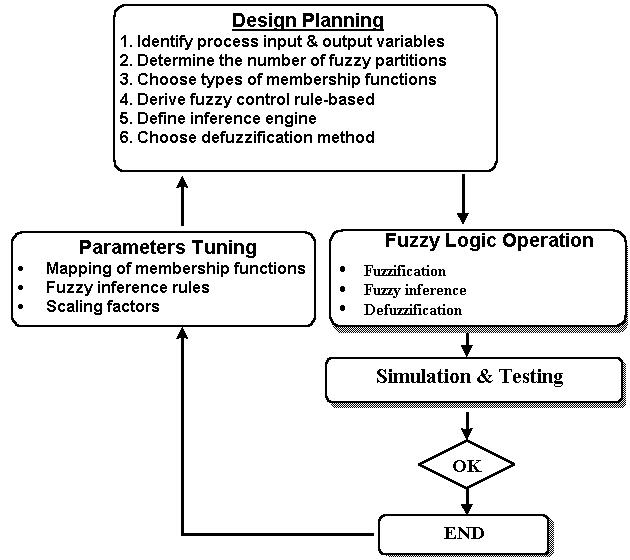For example, in addition to being either true or false, an outcome might have such meanings as probably true, possibly true, possibly false, and probably false. The design of fuzzy logic controller will base on the methodology as shown below.

Fuzzy Sets
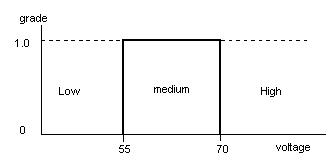
The very basic notion of fuzzy systems is a Fuzzy (sub)set. In classical mathematics we are familiar with what we call crisp sets. A classical set may be defined as by crisp boundaries where the boundary of a crisp set is an unambiguous line. However, fuzzy set is a set without crisp that clearly defined the boundary. Therefore, a fuzzy set can contain elements with only a partial degree of the set.

In classical set theory, a subset U of a set S can be defined as a mapping from the elements of S to the elements of the set {0, 1},    U: S --> {0, 1}
This mapping may be represented as a set of ordered pairs, with exactly one ordered pair present for each element of S. The first element of the ordered pair is an element of the set S, and the second element is an element of the set {0, 1}.  The value zero is used to represent non-membership, and the value one is used to represent membership.  The truth or falsity of the statement "x is in U" is determined by finding the ordered pair whose first element is x.  The statement is true if the second element of the ordered pair is 1, and the statement is false if it is 0.

Similarly, a fuzzy subset F of a set S can be defined as a set of ordered pairs, each with the first element from S, and the second element from the interval [0,1], with exactly one ordered pair present for each element of S. This defines a mapping between elements of the set S and values in the interval [0,1].  The value zero is used to represent complete non-membership, the value one is used to represent complete membership, and values in between are used to represent intermediate Degrees of Membership.  The set S is referred to as the Universe of Discourse for the fuzzy subset F.  Frequently, the mapping is described as a function, the Membership Function of F. The degree to which the statement " x is in F" is true is determined by finding the ordered pair whose first element is x.  The Degree of Truth of the statement is the second element of the ordered pair. In practice, the terms "membership function" and fuzzy subset get used interchangeably.
 

Crisp Sets

Fuzzy sets of low, medium and high

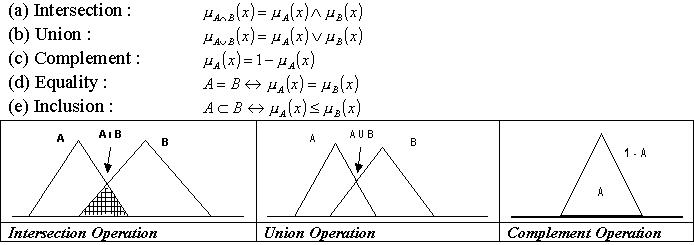
Operations of the Fuzzy Set
The five basic operators for fuzzy sets are intersection or conjunction (AND), union or disjunction (OR), complement (NOT), inclusion and equality. Let A and B be fuzzy subsets of X and below are the definition of these operators performed on fuzzy sets.

Linguistic Variables
Fuzzy logic is a powerful problem-solving methodology that can transform or model the uncertainty of natural language or vague concepts such as "very hot", "slightly", "quite slow", "low" and "rather warm" into a mathematical form which is then process by computers to solve and perform problem-solving actions. This problem-solving methodology allows computers to perform nearly like a human being's ability to think and reason.

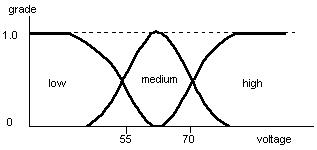
Membership Functions
A membership function (MF) is a curve that characterized the fuzziness in a fuzzy set in a graphical form that defines how instant input is mapped to the grade. The crisp input is called as universe of discourse. If X is the universe of discourse and its elements are denoted by x, then a fuzzy set A in X is defined as a set of ordered pairs:
A = {x, m_A(x) | x Î X}. m_A(x) is called the membership function of x in A. The membership function maps each element of X to a membership value between 0 and 1.
The membership functions which are often used in practice include triangular, trapezoidal, gaussian, sigmoidal, p, S and Z membership functions.

Fuzzy Rules
Fuzzy rules are a set of conditional statements as shown below:
  IF x is big THEN y is small
Fuzzy control rules are characterised by a collection of fuzzy IF-THEN rules which the antecedents and consequent involve linguistic variables. This collection of fuzzy control rules characterises the simple input-output relation of the system. The general form of the fuzzy control rules in the case of multi-input single output system (MISO) is " Ri : IF x is Ai, …, AND y is Bi, THEN z = Ci,  i = 1,2,…,n"
where x,…,y and z are linguistic variables representing the process state variables and the control variables. Ai,…,Bi and Ci are linguistic values of linguistic variables x,…,y and z in the universes of discourse U,…,V and W, respectively.

 To interpret the above fuzzy if-then rule, it involves two processes. The first process is to evaluate the antecedent which involves fuzzification to change a crisp input value to a degree of membership between 0 and 1. If the antecedent only consists of one fuzzy variable then this degree is the degree of support for the rule. If there are multiple fuzzy variables in antecedent, fuzzy operators is applied to obtain a single degree. The second process is the application of implication method in the consequent of the rule. If the antecedent is partially truth then the output fuzzy set in consequent is truncated according to the implicated method.

Fuzzy Inference
For application of approximate reasoning in fuzzy logic control, the generalised modules can be written as below:
Premise 1 :  IF x is A, THEN y is B.
Premise 2 :  x is A`
Conclusion : y is B`
where A, A`, B, B` are fuzzy sets in the universal sets U, U, V and V respectively.
There are four types of compositional operators that can be used in the compositional rule of inference:
· Max-min operation
· Max-product operation
· Max bounded product operation
· Max drastic product operation
In fuzzy control application, Max-min and Max-product composition operations are the most commonly used due to their computational simplicity and efficiency.
 

	Fuzzy Logic Resources
	A complete aceess to Fuzzy Logic knowledge....
	This web server comprises a complete repository for Fuzzy Logic and NeuroFuzzy applications. It contains free simulation software, case studies, and product information.
	Find out more about our pioneering technologies for the web.  This web provides the current and future direction for business.

Genetic Algorithm
The following was extracted from:  Genetic Algorithms and Artificial Neural Networks
A talk presented to the Fort Worth, Texas chapter of the Association for Computing Machinery, Spring 1988
Copyright 1988, 1992 by Wesley R. Elsberry

What is a genetic algorithm?
A genetic algorithm is an iterative search technique premised on the principles of natural selection.
A genetic algorithm is an implementation of a search technique which locates local maxima. Is it a state-space search or does it search surfaces? It does both.

What use is a genetic algorithm?
In searching a large state-space, multi-modal state-space, or n-dimensional surface, a genetic algorithm may offer significant benefits over more typical search or optimization techniques (linear programming, heuristic, depth-first, breadth- first, praxis, DFP [De Jong, 80]). Of course, 'boy-with-a- hammer' syndrome should be avoided.

Genetic algorithm components
a goal condition or function
a group of candidate structures (bit-maps, messages, weights, etc.)
an evaluation function which measures how well the candidates achieve the goal condition or function reproduction function (takes current candidates and reproduces them with some amount of variance)

Genetic Algorithm Sequence of Events
repeat
   1.evaluate current candidates
   2.develop new candidates via reproduction with modification which replace least-fit former candidates
until satisfied (where 'satisfied' indicates that the goal condition has been met, or that some failure condition is triggered, or never. 'Repeat forever' would be useful for adaptive systems.)

Why does this work?
     competition for system resources
     heritability of variance

How does this work? Example [from Smith, 88]:
State goal condition as finding binary string of length 5 with (4) 1's
Randomly generate L5 strings (length five), population size of 5
00010 (eval: 1)
10001 (eval: 2)
10000 (eval: 1)
01011 (eval: 3)
10010 (eval: 2)
Population evaluation average: 1.8
To find next generation, reproduce from this candidate population with modification. Modification method is defined as 'crossover', as in sexual reproduction.

Modification methods thus far proposed for GA's:
   1.crossover - interchanges strings at random point
   2.inversion - generates new schemata by flipping substring
   3.mutation - point mutation
Reproductive function semi-randomly selects pairs of candidate strings for production of new candidates. A random number is generated and applied to a selectionist distribution of candidate strings.

Selectionist distribution:
1 00010 (eval: 1)
2 10001 (eval: 2)
3 10001 (repeat since fitness is higher)
4 10000 (eval: 1)
5 01011 (eval: 3)
6 01011 (repeat)
7 01011 (repeat)
8 10010 (eval: 2)
9 10010 (repeat)

Select pairs (indices from selectionist distribution):
1 & 4 Then crossover point: 1
4 & 5 4
9 & 7 3
8 & 6 1
7 & 5 1

Result from :
1+4:1 = 00000 (eval: 0)
4+5:4 = 10001 (eval: 2)
9+7:3 = 10011 (eval: 3)
8+6:1 = 11011 (eval: 4)
7+5:1 = 01011 (eval: 3)
New population evaluation average: 2.4

The goal condition has now been satisfied, and the procedure ends.

How well do GA's work?
Given candidates which are binary strings:
Population size N
Number of generations G
We sample NG points out of 2^l where l is binary string length

So what?
This can be done with random search methods
But GA's develop a pool of genes
Search is for 'schemas' which are 'blocks' or 'alleles' (portions of the binary string which tend to be reproduced as a unit)
2^l schemas per individual
N*2^l schemas per population

What applications can this be put to?
     Accomplished:   adaptive systems design,  adaptive control,  finite automata specification,  optimization problems (TSP [Brady, 85])
     Projected:            parameter specification for neural networks

Problems:
     How to specify a 'genetic' pattern for the application in mind?
     Does it converge faster than learning procedures?
The example brought up by Smith was that of specifying weights in a back-propagation ANN. The question was raised as to whether the GA would show any advantage over just going ahead and doing the typical training. Since training involves the solving of sets of differential equations for each weight in the network, repeated over multiple training iterations, it is expected that GA's would produce significant time benefits. The GA does not require intensive computation, so more time could be spent in the evaluation phase. The GA would be more space-intensive, however, in order to maintain a 'population' of candidate weights for the back-propagation ANN.

Background:
Genetic algorithms are premised on the principles of natural selection in biology. In searching for a solution state, a 'population' of candidate states are generated, evaluated, selected, and reproduced with modification to produce the next candidate population.

(BA == Biological analogue)
Structures and modules needed:
     candidate data structures (BA = organisms)
     representation structure (BA = set of chromosomes)
     evaluation function (BA = environment)
     selection mechanism (BA = [too many to list])
     reproduction mechanism (BA = genetics)

In biology, the sequence of events works like this:
The organism has a set of structures which help determine its internal organization and capabilities. These are the genes, which in combination with environmental factors during development specify the formation of structures and connections. At maturity, the organism will have expressed a suite of characteristics which enable it to survive in its environment and propagate itself. The mode of reproduction which produces the most variance in the resulting offspring is sexual reproduction, which mixes genes from separate individuals to form the resulting offspring. Asexual reproduction is subject to variation only through external disturbances, such as
radiation induced mutation or viral transcription, which produce variations that are small or relatively infrequent.

Various expressed characteristics of an organism may make it less successful than other organisms of the same species, where success is defined as 'differential reproductive success', in other words, the organism leaves more related offspring than those which do not demonstrate the same degree of adaptation. The next generation of organisms then proceed through the same processes.

The expressed characteristics of the organism are not necessarily the same characteristics as those coded for in the genes of the organism. The actual set of gene information is referred to as the genotype, while the expressed characteristics of the organism is referred to as the phenotype. The difference between code and expression can be a result of both the environmental factors and the interaction between genes on a pair of chromosomes.

Why genetic algorithms? Why, for that matter, neural networks? Both of these active research fields are premised on aspects of biological phenomena. Consider the complex problems which living systems must contend with in order to survive. The highly diverse fauna currently living gives some idea of the range of possible solutions to these problems. However, that is not the entire picture. Consider the currently extant number of species to be a small subset of instances in a far larger solution space.

The existing species can be thought of as representing 'splotches' on the surface of an expanding hypersphere. By no means do they represent the entire range of possible solutions. These species are postulated to have arisen by the process of natural selection.
Natural selection provides a mechanism for the identification and propagation of appropriate adaptation to specific and complex problems. Basically, natural selection can be described cursorily in the following manner. Several conditions are postulated.
     a population of candidate entities
     within this population, there is variation
     some of these variations are heritable
     the individuals of the population are capable of reproduction, either by themselves or in conjunction with other individuals
     the individuals within the population are constrained by the environment
     stresses in the environment may prove debilitating or fatal to the individual
     limitations on resources provided by the environment will prevent the unrestricted propagation of individuals of the population
     limitations induce competition between individuals of the population for resources
     individuals compete for basic resources:
     elements or compounds necessary for basic processes of metabolism
     elements, compounds, or structures which provide food
     other individuals for the purpose of reproduction ( in sexual reproduction )
     a mechanism for the introduction of variation exists
     within the context of DNA or RNA based heritability, point mutations may occur through the action of radiation of suitable energy (gamma ray, X-ray, UV light). For asexually reproducing species, this will be one of the major sources of variation.

With these postulated requirements, natural selection proceeds. The variation in individuals will lead to differences in the success of individuals, where success is defined to be differential reproductive success.
heritable traits which confer differential success will tend to become more highly represented in the population
    heritable traits which are maladaptive will tend to become less well represented in the population

Notice that the selection process is not considered to 'favor' adaptive characteristics, rather, relatively maladaptive or nonadaptive traits are 'selected' against. Thus, natural selection can be considered to include a normalization procedure. The variation which is present in the population is generally assumed to arise at random. The selection process, however, is not random, but is premised on  relative functionality with reference to the absolute constraints of the environment.
 
 

	Genetic Algorithm Resources
	The Genetic Algorithms Archive is a repository for information related to research in genetic algorithms and other forms of evolutionary computation.
	Enter here to view the graphical version of the genetic algorithm

Back To Top