Prev Up Top Next Contents
2.B Fisica delle cadute
In questa appendice cerchiamo di descrivere le
cadute in termini fisici, al fine di fornire gli elementi di base
per una comprensione dei rischi che incorrono
[
247] [
248] [
249] [
250] .
In caso di caduta il corpo umano riduce la forza massima di circa
il 20% assorbendo parte dell'energia [
138] .
Altri rischi, inerenti la velocita` e la possibilita`
di urti [
251] , non sono qui considerati.
2.B.1 Forza di arresto
Quando si cade la corda deve bloccare la caduta.
Tuttavia, non deve fermarci troppo in fretta, altrimenti il nostro
corpo sarebbe soggetto ad una violenta decelerazione, che e` come
andare a sbattere contro un muro. E` per questo che sulle vie ferrate
si usano i dissipatori, per distribuire l'urto della fermata.
D'altra parte non deve neppure essere troppo elastica, altrimenti
c'e` maggior pericolo d'urto contro la roccia.
E` stato appurato che la massima accelerazione sostenibile dal corpo
umano e` 15 g (15 volte l'accelerazione di gravita`), se si cade
verticali, a testa in su` [
138] .
Se si cade a testa in giu` il corpo puo`
sopportare solo 2-3 g. I problemi in caso di forti accelerazioni sono
l'aumento di pressione in alcuni vasi con conseguente danneggiamento
di organi interni.
Supponiamo che uno spelelologo cada su una corda per una lunghezza
H
e che la corda si allunga di
A
perche` e` elastica e viene tirata dallo spelelologo in caduta.
Il lavoro immagazzinato nella corda non e` dunque la sola
caduta su una lunghezza
H, ma su una lunghezza
H+A.
Questo cambia leggermente la formula, che risulta, nel caso di caduta
rettilinea (dalla ugualianza fra l'energia della caduta e quella nella
tensione della corda) [
15] [
70] ,
Fmax = P + ( P2 + 2 Fc P/X )1/2
La forza d'arresto cresce con P (come la radice quadrata
di P per piccoli valori, che e` il caso dello speleologo che cade).
Diminuisce al crescere della elasticita` X (ricordo che
dL = P L X), ed aumenta al crescere del fattore di caduta,
Fc= H/L.
Nel caso di P <2 Fc/X , cioe` nel caso dei "voli"
per noi speleologi, si puo` approssimare
Fmax = (2 Fc P / X)1/2.
Risultati piu` dettagliati si possono ottenere impostando
le equazioni della dinamica di una caduta.
La caduta du un tratto di corda puo` essere modellizzata con un
comportamento elasto-dissipativo della corda (
K costante elastica,
R dissipazione) [
252] . L'equazione della dinamica e`
M Z" + R Z' + K (Z - Zo) = M g
La dissipazione di energia all'interno dalla corda e` proporzionale
alla sua velocita` di allungamento, quindi alla velocita` dello
speleologo. La forza elastica e` proporzionale all'allungamento
della corda, mentre la costante elastica e` inversamente proporzionale
alla lunghezza della corda.
Questa equazione diventa (z=Z-Z
o, r=R/M, k=K/M)
z" + r z' + k z = g con condizioni iniziali
z(0)=0 e z'(0)=v
o=(2gH)
1/2.
La soluzione di questa equazione e`
z(t)= g/k + A exp([-s+iw]t) + B exp([-s-iw]t)
= g/k [1-e-stcos(wt)] + (vo-sg/k)/w e-stsin(wt),
cioe` delle oscillazioni smorzate.
La costante di smorzamento vale s=r/2 e la
frequenza delle oscillazioni e` w2=k - s2.
La massima accelerazione sullo speleologo, cioe` la massima
forza di arresto, risulta quando la velocita` si annulla
(per la prima volta)
amax = [ g2 - 2 g s vo + k vo2 ]1/2
exp( - s to )
dove il tempo t
o e` tale che la velocita` si annula,
exp(2iwt) = -(B/A)(s+iw)/(s-iw).
Il termine esponenziale e` sempre inferiore ad 1 e, come il secondo
termine nell'espressione sotto radice, tiene conto della dissipazione
di energia nella corda. Quindi l'accelerazione massima e` inferiore
a ( g
2 + 2 g k
o H/L )
1/2, cioe` il risultato semplificato
trovato sopra in base a considerazioni energetiche.
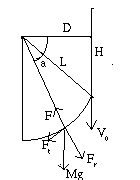
Fig. 74. Caduta: diagramma delle forze
In generale la caduta non e` rettilinea, perche` non si cade proprio
sotto (o sopra) l'ancoraggio.
Percio` si ha una caduta libera fino a che la corda non entra in tensione.
Dopodiche` si descrive un arco.
Fr = M g sin(a) - F
Ft = M g cos(a)
dove
F(r)=(r-L)/(LX) e` la tensione nella corda.
Le equazioni dinamiche possono essere facilmente impostate
d2 r/dt2 - r (da/dt)2 = g sin(a) - (r-L)/(LX)
r d2 a/dt2 + 2 dr/dt da/dt = g cos(a)
con condizioni iniziali
r(0)=L,
a(0)=a
o = arccos(D/L),
v(0)=v
o = (2 g H)
1/2,
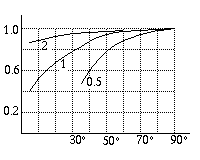
Fig. 75. Forza massima
Conviene stimare l'energia assorbita dalla corda come somma di due termini:
energia cinetica radiale (che tende direttamente la corda)
e quella tangenziale (che produce durante la rotazione una accelerazione
centrifuga la quale va a tendere la corda).
Quando la corda entra in tensione si ha
Er,o = ½M (vo sin(ao))2
Et,o = ½M (vo cos(ao))2
dove
vo = (2 g H)
1/2.
Nel seguito della caduta (lungo l'arco) l'energia potenziale viene
perlopiu` convertita in moto tangenziale, per cui quando si arriva nel punto
piu` basso l'energia tangenziale e` diventata
Et = Et,o + P L (1 - sin(ao) )
A questa corrisponde una forza centrifuga (approssimativamente)
Ft = 2 Et / L
= 2 P (1 - sin(ao) ) + 2 P (H/L) cos2(ao)
Il fattore di caduta e`
Fc = (H + L ( 1 - sin(ao ) ) ) / L
La forza massima e` dunque stimabile come
Fmax =
[ 2 P/X (Fc - 1 + sin(ao) )
sin(ao) + 2 P ( 1 - sin(ao) ]1/2
( sin2(ao + Fc ( 1 + sin(ao) )
Questo risultato e` riportato nella figura a destra, rapportato
alla forza massima per caduta verticale (quando sin(
ao)=1)
nel caso 2
P X=100 (che e` un poco eccessivo), e a diversi fattori
di caduta.
Come si vede la forza massima in caso di caduta fuori dal punto di
ancoraggio e` sempre inferiore al caso verticale (anche se induce
una oscillazione che puo` essere pericolosa per altri versi !).
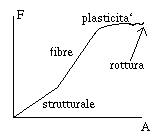
Fig. 76. Diagramma forza-allungamento
In pratica le corde da speleologia, hanno elasticita` strutturali
(dovute al fatto che sono costruite con un'anima a trefoli intrecciati,
ed una calza che li contiene) oltre che ad una elasticita` delle fibre
(di nylon).
Percio` la relazione fra l'allungamento e la forza non e` lineare:
nel primo tratto intervengono sia l'elasticita` strutturale che
quella delle fibre, percio` la corda e` "molto" elastica.
Quando la struttura ha esaurito la sua elasticita`, resta solo
quella delle fibre, fino a che non inizia la regione di deformazioni
irreversibili (plasticita`) che preclude alla rottura della corda.
In questo discorso non viene considerata l'energia assorbita
da altri elementi, come i nodi, l'imbrago e i movimenti
del corpo dello speleologo.
In particolare la forza massima di arresto risulta inferiore di circa
il 30% al valore teorico.
Nelle cadute sulle longe parte dell'energia viene (fortunatamente)
dissipata nella compressione delle spire dei due nodi alle estremita`
(
effetto longe [
138] ).
2.B.2 Composizione di piu` elementi
In generale un ancoraggio non e` fatto dalla sola corda, ma da tanti elementi
(piastrina, bullone, moschettone, nodo, corda, attrezzi, ...)
ognuno con la sua elasticita`, e tutti concorrono a dissipare l'energia
di una caduta.
Occorre stimare l'elasticita` di tutto l'insieme al fine di valutare
la forza d'arresto, e la forza massima che agisce su ciascun
elemento, per giudicare la tenuta dell'ancoraggio.
Partiamo da due semplici casi:
- elementi connessi in serie;
- elementi connessi in parallelo.
Casi piu` complicati si possono ricondurre a questi casi elementari.
Nel primo caso (elementi in serie) si vede, da considerazioni
energetiche, che ogni elemento contribuisce all'elasticita` globale
proporzionalmente alla sua lunghezza ed elasticita`,
X = (X1 L1 + X2 L2 + X3 L3 + ... )
/ ( L1 + L2 + L3 + ... )
Percio`
X e` determinato dagli elementi piu` elastici e piu` lunghi
(solitamente la corda).
La forza d'arresto e` uguale per tutti gli elementi:
Fmax = (2 F
c P / X)
1/2.
Nel secondo caso risulta
X = ( 1/X1 + 1/X2 + ...)-1
Percio` l'elasticita` e` inferiore a quella di ogni singolo elemento.
La disposizione in parallelo accresce la rigidita` del sistema.
Conseguentemente la forza d'arresto (dell'intero sistema) e` superiore
rispetto a quella che si avrebbe con un singolo elemento.
Tuttavia ogni singolo elemento deve sostenere una forza massima
inferiore. Dunque
formare anelli di corda comporta un aumento del carico di rottura
perche` la forza massima sul singolo giro di corda e` una frazione
della forza di arresto.
Quale esempio di sistemi di elementi elastici consideriamo due tipi di longe.
La longe formata da un anello di corda chiuso con un nodo (inglese doppio),
e la longe singola, con due nodi (ad otto) con gasse alle estremita`.
Trascuriamo i moschettoni.
La prima longe e` un parallelo di due elementi (uno dei quali e` una
serie di due elementi per la presenza del nodo). L'elesticita` risulta
(
X e` l'elasticita` della corda,
L la lunghezza della longe)
X1 = X / ( 1 + 1 / (1 - ln ( 1 - xn ) ) )
dove
ln e` il rapporto fra lunghezza del nodo e quella
della longe, e
xn e` il rapporto fra l'elasticita` del
nodo e quella della corda.
Nella longe singola abbiamo due gasse (elasticita`
X/2),
due nodi, e un pezzo di corda.
L'elasticita` e` (i nodi hanno approssimativamente la stessa lunghezza)
X2 = X ( 1 - lg - 2 ln (1 - xn) )
Ad esempio,
se prendiamo la longe corta, L = 18 cm, con gasse da 2 cm, e nodi da
6 cm, otteniamo che la longe doppia e` piu` elastica della longe semplice
(oltre a poter assorbire maggior forza d'arresto perche` e` un sistema
parallelo).
Quindi (almeno dal punto di vista teorico) la longe doppia e`
preferibile alle semplice.
2.B.3 Fisica della caduta su un traverso
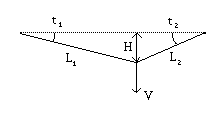
Fig. 77. Traverso: diagramma delle forze
Consideriamo le forze in giuoco quando si cade su un tratto di traverso.
Supponiamo, per semplicita`, che i due punti di ancoraggio sono
alla stessa altezza.
Con una caduta di lunghezza H la velocita` nel momento in cui
si tende la corda e` V = (2 g H)1/2 (e diretta verticalmente
perlopiu`). Essa e` anche la velocita` con cui viene sollecitata
la corda; puo` essere scomposta in due componenti lungo i due pezzi
di corda V1 nella direzione L1 e
V2 nella direzione L2.
Risulta
V1 = V cos(t2) / sin(t1 + t2)
V2 = V cos(t1) / sin(t1 + t2)
Percio` l'energia dissipata su ciascun pezzo di corda
(scriviamo solo la formula per il primo)
E1 = M g H cos2(t2) / sin2( t1 + t2 )
e la forza massima sull'armo
F1,max =
(2 M g H / X L1) cos(t2) / sin(t1 + t2 )1/2
= (2 M g / X)1/2
( sin(t1) / sin( t1 + t2 ) ) cos(t2)1/2
dove
X e` l'elasticita` della corda.
La formula nella seconda riga si riferisce ad una caduta dalla quota
della corda (come in figura).
In questo caso si vede che la forza massima su ciascun armo e`
comunque inferiore a (2 M g/X)
1/2 cioe` quella
di una caduta a fattore di caduta 1.
2.B.4 Recupero di un carico
Nel recupero di un carico l'inerzia del peso provoca delle oscillazioni
nella corda. Se il recupero avviene a velocita`
v costante, il
punto superiore della corda si muove con legge
v t, e quello
inferiore con la legge
- L - x(t) + v t. L'accelerazione su questo
risulta
-x"(t), per cui, eguagliando la forza di inerzia alla
tensione nella corda, si ha che esso esegue oscillazioni
x(t) = xo sin( w t )
con frequenza
w = 1 / (M L X)
1/2 e ampiezza
xo =
v/w. La forza massima sulla corda e`
M g +
v / (
X L w).
La tensione addizionale cresce al diminuire della
lunghezza
L e ad decrescere della elasticita`
X (cioe` per
corde piu` statiche).
Se il tiro viene ripetuto ad intervalli regolari, si puo` avere un effetto
di risonanza con oscillazioni sempre piu` grandi.
Per esempio se L = 50 m, M = 80 Kg,
X = 0.05 1/KN, risulta una frequenza di 2.2 Hz.
Lo stesso effetto dovrebbe succedere con delle pedalate regolari.
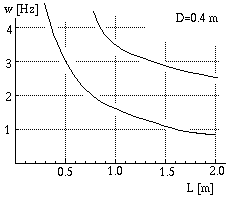
Fig. 78. Oscillazione del sacco
Un analogo fenomeno avviene quando il sacco appeso sotto si mette ad oscillare
fastidiosamente. In questo caso la frequenza e` quella di oscillazione
del sacco, che forma un pendolo composto.
Teoricamente la frequenza dipende dalla lunghezza L del
cordino (circa 1 m), da g=9.8 m/s2
e dalla lunghezza del sacco. In effetti anche dalla posizione del
centro di massa, e dal momento di inerzia, ma per semplicita` assumiamo
che sia come una sbarra rigida, di lunghezza 2 D,
per cui il centro di messa si trova
nel mezzo e il momento di inerzia vale I = M D2 / 3.
Questo sistema ha due frequenze fondamentali, che hanno forma
w = (g / (L (1 - c/2)))1/2
dove
c e` una delle soluzioni della equazione di secondo grado
c2 - 2 (1 - 4/3 D/L ) c - D/L.
Una delle due frequenze e` inferiore a quella del pendolo semplice,
(g/L)
1/2, l'altra e` superiore.
Da questa analisi concludiamo che per evitare noiose oscillazioni del sacco
occorre accorciare il cordino. In tal modo anche se aumenta il rapporto
D/L e la frequenza bassa tende al valore del pendolo semplice,
questa diventa abbastanza alta da evitare oscillazioni in risonanza.
In pratica le oscillazioni del sacco risultano indipendenti da come
esso viene attaccato all'imbrago, dal suo peso, e dalla lunghezza
del cordino [
56] . Essa sono dovute all'elasticita` della
corda che induce oscillazioni verticali, e, soprattutto, ai
movimenti trasversali del bacino dello speleologo (cioe` del punto
di attacco del sacco).
marco corvi - Mon Nov 19 11:34:13 2007
Prev Up Top Next Contents
This work is licensed under a Creative Commons
Attribution-NonCommercial-ShareAlike 2.0 Italy License.




