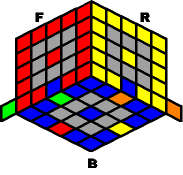
Before
N- B- N+ B2
N- B- N+
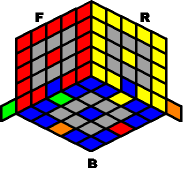
The remaining 4 inner-edges are already on the bottom layer, where they belong. The first step is to arrange them in the correct positions. At this point, there are three possibilities:
If NO inner-edge is in place, then use the sequence below:

Before |
N- B- N+ B2 |

After |
You only need to do this sequence once.
Note: Ignore the diagrams. As long as you keep the original top face on the top side, this sequence will guarantee that at least ONE bottom inner-edge will land in place afterwards.
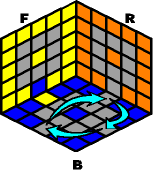
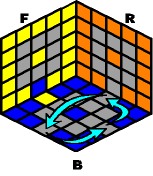
If only ONE inner-edge is in place, then rotate the entire puzzle until the fixed inner-edge piece appears on the bottom front. The remaining 3 inner-edges need to be swapped either clockwise or counter-clockwise.
Exchange |
Exchange |
|
 |
 |
|
N- B+ N+ B2 |
N- B- N+ B2 |
You only need to memorize one of the above. For example, if you choose to memorize the "counter-clockwise" sequence, then use it twice to swap the 3 edges clockwise. Once all 4 inner-edges are arranged in place, get ready for the last step: INVERSION.
There are 3 different inversion schemes:
For each inversion scheme, you must rotate the entire puzzle so that the inverted edges are positioned exactly like the ones in the diagrams, before attempting the sequence of moves!
~~~~ Case #1: Invert two adjacent edges ~~~~ |
||||
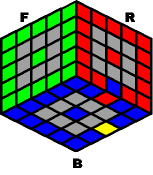 |
N- B- N+ B- |
Result: |
||
______________________________ |
||||
~~~~ Case #2: Invert two opposite edges ~~~~ |
||||
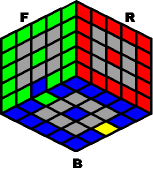 |
N- B- N+ B- |
Result: |
||
______________________________ |
||||
~~~~ Case #3: Invert all four edges ~~~~ |
||||
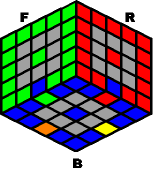 |
N- B- N+ B- |
Result: |
||
As it turns out, the same sequence was used throughout all three cases.
Now that all the bottom edges are solved, the only thing left are the
Middle and Bottom Faces.