The Professor's Cube

I. Solve the Top Center Face

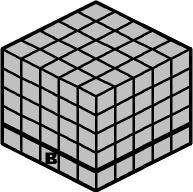
Welcome to the Professor's Cube solution, the is the Grand-daddy of 'em all. There are 92 pieces you have to solve:

• 8 corners
• 24 outer edges
• 12 inner edges
• 24 outer faces
• 24 inner faces

The 6 center faces are fixed, and they define what color each side will eventually become. They can rotate in place, but can never jump from face to face.

Q: Is my brain going to explode?

A: No. Most of the moves used for this solution should already be familiar to you; the notation may be somewhat different (due to the extra slices and layers), but you should recognise the same feel of it. For example, the method for solving all corners is identical to the moves found in the Rubik's Cube and Revenge solution. With exception, the outer-edges follow the same method as the 4x4x4 solution, while the inner-edges mirror the 3x3x3. Some of the moves have been modified for reasons I will explain later. Basically, all you are doing is solving a Regular and Revenge cube at the same time.

Anyway, let's get on with the top faces...

Pick a favorite color as the top side.		Solve the top inner-faces first		Solve the top outer-faces last

I am not going to decribe how to do this, as this should be intuitive and easy enough for anyone to do. However, you must choose what the top side is, and which color to use. After that, the top side stays on top for the rest of the solution.

Note: It is not necessary to solve all 4 inner faces before solving the next 4 outer-faces. You can solve the 8 pieces in any order you please. Yet, the easiest way is to follow the diagrams.

Notation:

There are fifteen layers in the Professor's Cube, but we only need to concern ourselves with seven of them; the five vertical slices (Left, M, N, O and Right), the bottom layer (B) and the front side (F).

• L+ ...move the LEFT slice UP (1/4 turn)
• L- ...move the LEFT slice DOWN (1/4 turn)

• M+ ...move the 'M' slice UP (1/4 turn)
• M- ...move the 'M' slice DOWN (1/4 turn)

• N+ ...move the 'N' slice UP (1/4 turn)
• N- ...move the 'N' slice DOWN (1/4 turn)

• O+ ...move the 'O' slice UP (1/4 turn)
• O- ...move the 'O' slice DOWN (1/4 turn)

• R+ ...move the RIGHT slice UP (1/4 turn)
• R- ...move the RIGHT slice DOWN (1/4 turn)

• [MNO]+ ...move the middle three vertical slices (M,N&O) UP
• [MNO]- ...move the middle three vertical slices (M,N&O) DOWN

• B+ ...move the BOTTOM layer RIGHT (1/4 turn)
• B2 ...move the BOTTOM layer HALF-WAY AROUND (1/2 turn)
• B- ...move the BOTTOM layer LEFT (1/4 turn)

• F+ ...move the FRONT side CLOCKWISE (1/4 turn)
• F2 ...move the FRONT side HALF-WAY AROUND (1/2 turn)
• F- ...move the FRONT side COUNTER-CLOCKWISE (1/4 turn)

NEXT: Solve the Top Corners...

@ Notation / Top Face
@ Top Corners @ Top Outer-Edges @ Top Inner-Edges
@ Middle Outer-Edges @ Middle Inner-Edges
@ Bottom Corners @ Bottom Outer-Edges @ Bottom Inner-Edges
@ Middle & Bottom Faces

Return to Mathematica