The Professor's Cube

III. Solve the Top Outer Edges

All outer-edges have a strange property; half of them are "left-handed", while the other half are "right-handed". If a left-hand edge lands on a right-hand spot (or visa-versa), it gets inverted. Otherwise, it is correctly polarized. Anyway, now that trivia time is over, let's get back to the solution...

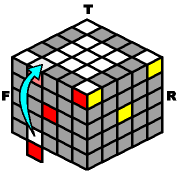
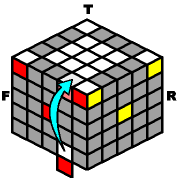
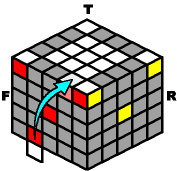
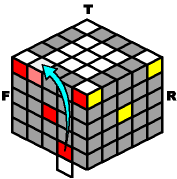
Here are 4 ways to get an outer-edge from the bottom to the top. Rotate the bottom layer until the outer-edge appears in the front, and then get ready to climb it to the top. Make sure the color patterns match before moving a single slice.

~~~~ Move Up (from the bottom): ~~~~
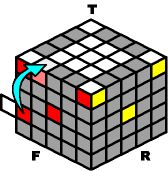
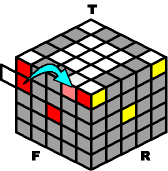
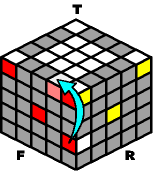
B- M- B+ M+		B+ O- B- O+		O- B2 O+ B+ O- B- O+		M- B2 M+ B- M- B+ M+

An outer-edge can also appear at the "equator" of the puzzle. It can start from four different places, so once again there are four different moves to navigate it to the top. You may have to rotate the top layer to match the diagrams below.

~~~~ Move Up (from the equator): ~~~~
M- B- L- B+ M+ B- L+		O- B- L- B+ O+ B- L+		M- B+ R- B- M+ B+ R+		O- B+ R- B- O+ B+ R+

Note: these moves are optional and are provided only as shortcuts. You can bypass this section by knocking an edge down from the equator (next section), and moving it up to the top layer (previous section) afterwards. On the plus-side, you have less moves to memorize. On the minus-side, you have to do twice as much work.

Knock Down:

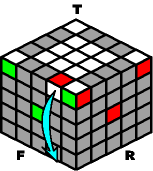
The outer-edge you want to move may not always on the bottom layer. Sometimes it can appear at the equator of the puzzle; other times it can already be on the top layer, but on the wrong side. Either way it must be knocked down, so you can climb it up to the correct spot later on.

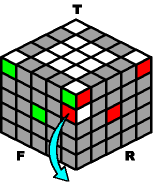
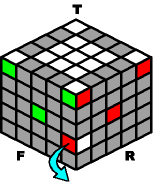
~~~~ Knock Down (from the top): ~~~~				~~~~ Knock Down (from the equator): ~~~~
M- B- M+		O- B+ O+		O- B- R- B+ O+ B- R+		M- B- R- B+ M+ B- R+

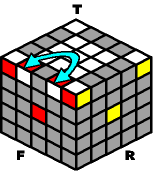
And finally, if you need to invert a pair of outer-edges that are already on top:

~~~~ Invert: ~~~~
		M- O- B2 M+ O+ B- M- O- B+ M+ O+

Go ahead and solve the other top outer-edges. You will not disturb any of the others that are already fixed in place. As a matter of fact, you will not disturb any cubelet on the top face, whether it is solved or not. Now you can proceed to solve the
Top Inner-Edges.

@ Notation / Top Face
@ Top Corners @ Top Outer-Edges @ Top Inner-Edges
@ Middle Outer-Edges @ Middle Inner-Edges
@ Bottom Corners @ Bottom Outer-Edges @ Bottom Inner-Edges
@ Middle & Bottom Faces

Return to Mathematica