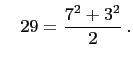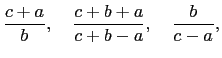 and
and 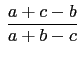
(each fraction reduced to lowest terms) is equal to
Proof.
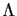
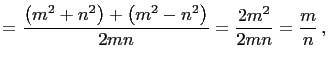 |
||
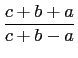 |
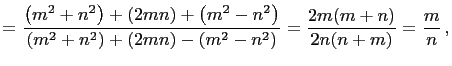 |
|
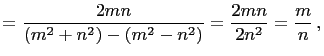 |
||
and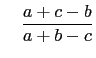 |
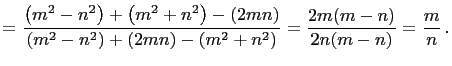 |
This section in pdf form. triplesmn.pdf
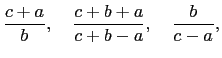 and
and 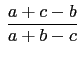
(each fraction reduced to lowest terms) is equal to
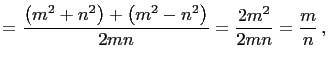 |
||
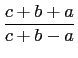 |
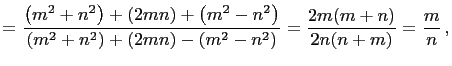 |
|
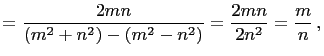 |
||
and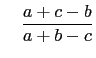 |
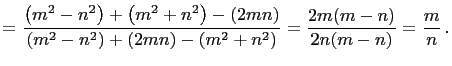 |
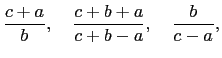 and
and 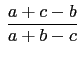
(each fraction reduced to lowest terms) is equal to
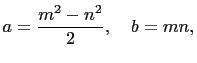 and
and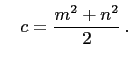
So,
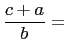 |
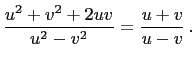 |
|
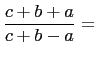 |
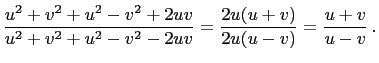 |
|
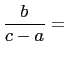 |
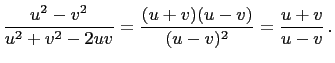 |
|
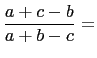 |
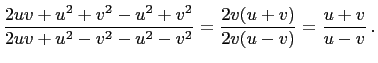 |
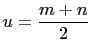 and
and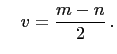
Hence, we have,
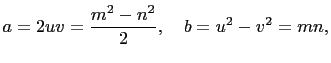 and
and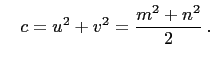
![]() is a primitive Pythagorean triple and 3 is
odd. So, let
is a primitive Pythagorean triple and 3 is
odd. So, let ![]() . Then
. Then
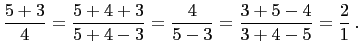
Hence
![]() is a PPT and 21 is odd. So
is a PPT and 21 is odd. So
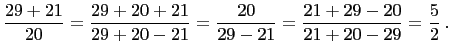
Hence,
![]() is a primitive Pythagorean triple and 4 is
even. So, let
is a primitive Pythagorean triple and 4 is
even. So, let ![]() . Then
. Then
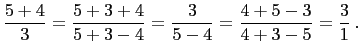
Thus
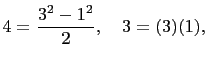 and
and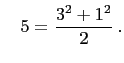
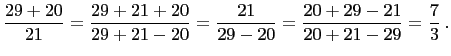
Therefore
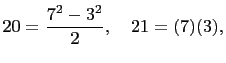 and
and